how to prove ((the volumn of dimensional sphare)) formula V


Question and Answers Forum

All Questions Topic List
Mensuration Questions
Previous in All Question Next in All Question
Previous in Mensuration Next in Mensuration
Question Number 97888 by M±th+et+s last updated on 10/Jun/20

$h o w t o p r o v e ((t h e v o l u m n o f$ $d i m e n s i o n a l s p h a r e)) f o r m u l a$ $V_{N} (R) = \frac{π^{N / 2}}{Γ (\frac{N}{2} + 1)} R^{N}$
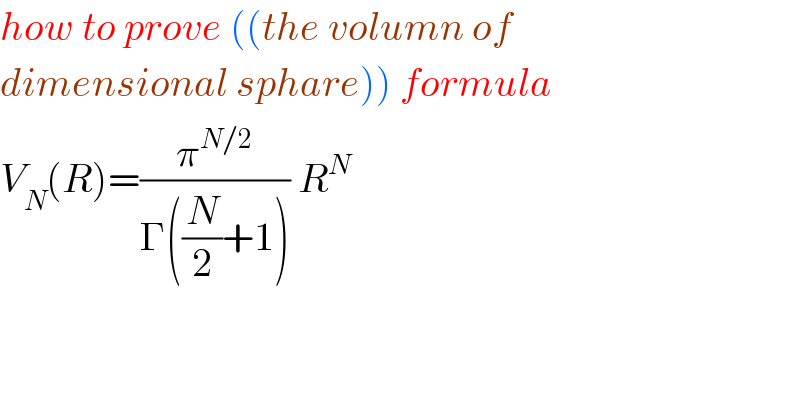
Commented by EmericGent last updated on 10/Jun/20
I think you can integrate N times, I'm sorry, I can't try it now
Commented by M±th+et+s last updated on 10/Jun/20

$t h a n k s f o r g i v i n g t h e i d e a m y b e i w i l l$ $t r y l a t e r$
	Answered by smridha last updated on 10/Jun/20

	$a t f i r s t c a l c u l a t e v_{N} (1) [v o l u m e o f u n i t c i r c l e i n N d i m]$ $t h e n m u l t i p y b y R^{N} .$ $y o u c a n u s e m u l t i d i m e n t i o n a l$ $c a l c u l u s a n d c o n s t r a c t e d J a c o b i a n$ $f o r N d i m e n t i o n .$ $y o u c a n s e e t h i s . . .$ $v o l u m e o f s p h e r e i n 3 D i s$ $\frac{4}{3} π R^{3} i n 2 D i t b e c a m e π R^{2} j u s t t h e$ $a r e a o f c i r c l e i n 1 D i t b e c a m e$ $2 R . . . . . .$ ${i t}^{'} s v e r y l e n g t h y p r o o f . . .$ $I c a n s o l v e t h i s . . . . t h a n k y o u . . .$
	Commented by M±th+et+s last updated on 10/Jun/20

	$t h a n k y o u v e r y m u c h s i r g o o d e x p l a i n i n g$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum