Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 97919 by Lekhraj last updated on 10/Jun/20

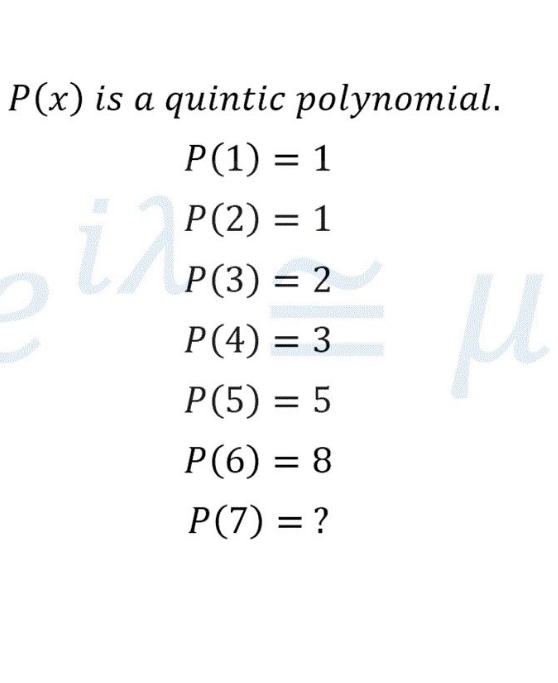
Commented by MJS last updated on 10/Jun/20

p(x)=ax^5 +bx^4 +cx^3 +dx^2 +ex+f insert the given pairs (x, p(x)) and solve for the constants ⇒ p(x)=−(x^5 /(40))+((11x^4 )/(24))−((25x^3 )/8)+((241x^2 )/(24))−((287x)/(20))+8 p(7)=8

$${p}\left({x}\right)={ax}^{\mathrm{5}} +{bx}^{\mathrm{4}} +{cx}^{\mathrm{3}} +{dx}^{\mathrm{2}} +{ex}+{f} \\ $$$$\mathrm{insert}\:\mathrm{the}\:\mathrm{given}\:\mathrm{pairs}\:\left({x},\:{p}\left({x}\right)\right)\:\mathrm{and} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{the}\:\mathrm{constants} \\ $$$$\Rightarrow \\ $$$${p}\left({x}\right)=−\frac{{x}^{\mathrm{5}} }{\mathrm{40}}+\frac{\mathrm{11}{x}^{\mathrm{4}} }{\mathrm{24}}−\frac{\mathrm{25}{x}^{\mathrm{3}} }{\mathrm{8}}+\frac{\mathrm{241}{x}^{\mathrm{2}} }{\mathrm{24}}−\frac{\mathrm{287}{x}}{\mathrm{20}}+\mathrm{8} \\ $$$${p}\left(\mathrm{7}\right)=\mathrm{8} \\ $$

Commented by mr W last updated on 10/Jun/20

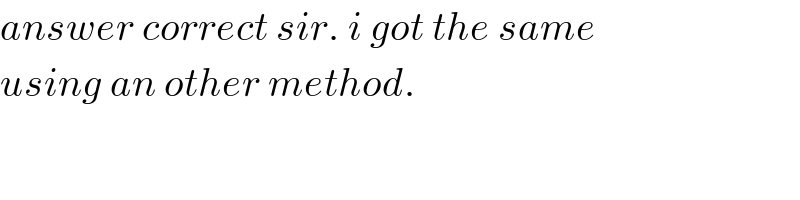
answer correct sir. i got the same using an other method.

$${answer}\:{correct}\:{sir}.\:{i}\:{got}\:{the}\:{same} \\ $$$${using}\:{an}\:{other}\:{method}. \\ $$

Answered by mr W last updated on 10/Jun/20

an attempt without solving eqn. and even without using a calculator: p(1)=1 ⇒p(x)=a(x)(x−1)+1 p(2)=a(2)(2−1)+1=1 ⇒a(2)=0 ⇒a(x)=b(x)(x−2) ⇒p(x)=b(x)(x−2)(x−1)+1 p(3)=b(3)(3−2)(3−1)+1=2 ⇒b(3)=(1/2) ⇒b(x)=c(x)(x−3)+(1/2) ⇒p(x)=[c(x)(x−3)+(1/2)](x−2)(x−1)+1 ⇒p(4)=[c(4)(4−3)+(1/2)](4−2)(4−1)+1=3 ⇒c(4)=−(1/6) ⇒c(x)=d(x)(x−4)−(1/6) ⇒p(x)={[d(x)(x−4)−(1/6)](x−3)+(1/2)}(x−2)(x−1)+1 p(5)={[d(5)(5−4)−(1/6)](5−3)+(1/2)}(5−2)(5−1)+1=5 ⇒d(5)=(1/(12)) ⇒d(x)=e(x)(x−5)+(1/(12)) ⇒p(x)={[{e(x)(x−5)+(1/(12))}(x−4)−(1/6)](x−3)+(1/2)}(x−2)(x−1)+1 p(6)={[{e(6)(6−5)+(1/(12))}(6−4)−(1/6)](6−3)+(1/2)}(6−2)(6−1)+1=8 ⇒e(6)=−(1/(40)) ⇒e(x)=−(1/(40))=constant, since p(x) is quintic. ⇒p(x)={{{−(1/(40))(x−5)+(1/(12))}(x−4)−(1/6)}(x−3)+(1/2)}(x−2)(x−1)+1 ⇒p(7)={{{−(1/(40))(7−5)+(1/(12))}(7−4)−(1/6)}(7−3)+(1/2)}(7−2)(7−1)+1 ={{{−(1/(20))+(1/(12))}3−(1/6)}4+(1/2)}30+1 ={−(4/(15))+(1/2)}30+1 =−8+15+1 =8

$${an}\:{attempt}\:{without}\:{solving}\:{eqn}. \\ $$$${and}\:{even}\:{without}\:{using}\:{a}\:{calculator}: \\ $$$$ \\ $$$${p}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\Rightarrow{p}\left({x}\right)={a}\left({x}\right)\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$$ \\ $$$${p}\left(\mathrm{2}\right)={a}\left(\mathrm{2}\right)\left(\mathrm{2}−\mathrm{1}\right)+\mathrm{1}=\mathrm{1} \\ $$$$\Rightarrow{a}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow{a}\left({x}\right)={b}\left({x}\right)\left({x}−\mathrm{2}\right) \\ $$$$\Rightarrow{p}\left({x}\right)={b}\left({x}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$$ \\ $$$${p}\left(\mathrm{3}\right)={b}\left(\mathrm{3}\right)\left(\mathrm{3}−\mathrm{2}\right)\left(\mathrm{3}−\mathrm{1}\right)+\mathrm{1}=\mathrm{2} \\ $$$$\Rightarrow{b}\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{b}\left({x}\right)={c}\left({x}\right)\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{p}\left({x}\right)=\left[{c}\left({x}\right)\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right]\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow{p}\left(\mathrm{4}\right)=\left[{c}\left(\mathrm{4}\right)\left(\mathrm{4}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right]\left(\mathrm{4}−\mathrm{2}\right)\left(\mathrm{4}−\mathrm{1}\right)+\mathrm{1}=\mathrm{3} \\ $$$$\Rightarrow{c}\left(\mathrm{4}\right)=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow{c}\left({x}\right)={d}\left({x}\right)\left({x}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow{p}\left({x}\right)=\left\{\left[{d}\left({x}\right)\left({x}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{6}}\right]\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right\}\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$$ \\ $$$${p}\left(\mathrm{5}\right)=\left\{\left[{d}\left(\mathrm{5}\right)\left(\mathrm{5}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{6}}\right]\left(\mathrm{5}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right\}\left(\mathrm{5}−\mathrm{2}\right)\left(\mathrm{5}−\mathrm{1}\right)+\mathrm{1}=\mathrm{5} \\ $$$$\Rightarrow{d}\left(\mathrm{5}\right)=\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\Rightarrow{d}\left({x}\right)={e}\left({x}\right)\left({x}−\mathrm{5}\right)+\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\Rightarrow{p}\left({x}\right)=\left\{\left[\left\{{e}\left({x}\right)\left({x}−\mathrm{5}\right)+\frac{\mathrm{1}}{\mathrm{12}}\right\}\left({x}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{6}}\right]\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right\}\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$$ \\ $$$${p}\left(\mathrm{6}\right)=\left\{\left[\left\{{e}\left(\mathrm{6}\right)\left(\mathrm{6}−\mathrm{5}\right)+\frac{\mathrm{1}}{\mathrm{12}}\right\}\left(\mathrm{6}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{6}}\right]\left(\mathrm{6}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right\}\left(\mathrm{6}−\mathrm{2}\right)\left(\mathrm{6}−\mathrm{1}\right)+\mathrm{1}=\mathrm{8} \\ $$$$\Rightarrow{e}\left(\mathrm{6}\right)=−\frac{\mathrm{1}}{\mathrm{40}} \\ $$$$\Rightarrow{e}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{40}}={constant},\:{since}\:{p}\left({x}\right)\:{is}\:{quintic}. \\ $$$$\Rightarrow{p}\left({x}\right)=\left\{\left\{\left\{−\frac{\mathrm{1}}{\mathrm{40}}\left({x}−\mathrm{5}\right)+\frac{\mathrm{1}}{\mathrm{12}}\right\}\left({x}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{6}}\right\}\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right\}\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow{p}\left(\mathrm{7}\right)=\left\{\left\{\left\{−\frac{\mathrm{1}}{\mathrm{40}}\left(\mathrm{7}−\mathrm{5}\right)+\frac{\mathrm{1}}{\mathrm{12}}\right\}\left(\mathrm{7}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{6}}\right\}\left(\mathrm{7}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right\}\left(\mathrm{7}−\mathrm{2}\right)\left(\mathrm{7}−\mathrm{1}\right)+\mathrm{1} \\ $$$$=\left\{\left\{\left\{−\frac{\mathrm{1}}{\mathrm{20}}+\frac{\mathrm{1}}{\mathrm{12}}\right\}\mathrm{3}−\frac{\mathrm{1}}{\mathrm{6}}\right\}\mathrm{4}+\frac{\mathrm{1}}{\mathrm{2}}\right\}\mathrm{30}+\mathrm{1} \\ $$$$=\left\{−\frac{\mathrm{4}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{2}}\right\}\mathrm{30}+\mathrm{1} \\ $$$$=−\mathrm{8}+\mathrm{15}+\mathrm{1} \\ $$$$=\mathrm{8} \\ $$

Commented by MJS last updated on 10/Jun/20

great! method using only subtraction and addition: 1 1 2 3 5 8 8 0 1 1 2 3 0 1 0 1 1 −3 −1 1 0 −4 2 −1 −4 −3 −3

$$\mathrm{great}! \\ $$$$\mathrm{method}\:\mathrm{using}\:\mathrm{only}\:\mathrm{subtraction}\:\mathrm{and}\:\mathrm{addition}: \\ $$$$\mathrm{1}\:\:\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{3}\:\:\mathrm{5}\:\:\mathrm{8}\:\mathrm{8} \\ $$$$\:\:\mathrm{0}\:\:\mathrm{1}\:\:\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{3}\:\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{1}\:\:\mathrm{0}\:\:\mathrm{1}\:\:\mathrm{1}\:−\mathrm{3} \\ $$$$\:\:\:−\mathrm{1}\:\:\mathrm{1}\:\:\mathrm{0}\:−\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}\:−\mathrm{1}\:−\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:−\mathrm{3}\:−\mathrm{3} \\ $$

Commented by mr W last updated on 10/Jun/20

nice illustration! i didn′t think of this.

$${nice}\:{illustration}!\:{i}\:{didn}'{t}\:{think}\:{of} \\ $$$${this}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com