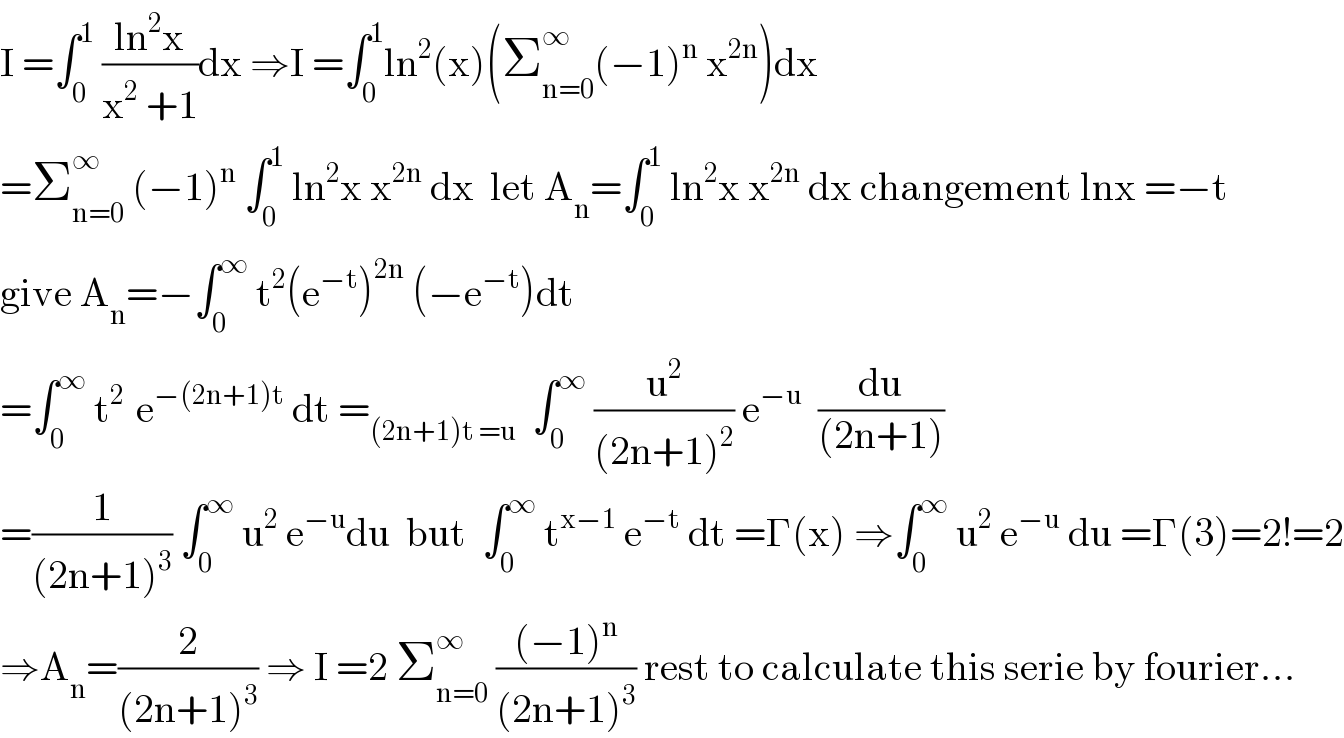Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 98016 by bemath last updated on 11/Jun/20

$$\underset{0}{\stackrel{1}{\int }}\frac{{\ln }^2\left(x\right)}{x^2+1}dx?$$

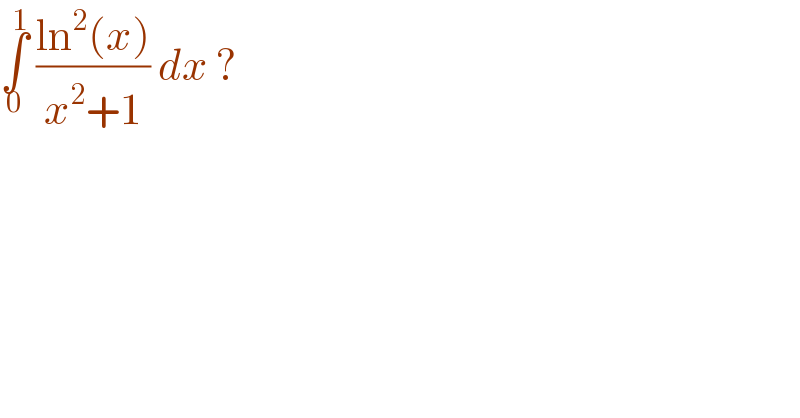
Commented by bobhans last updated on 11/Jun/20

$$\mathrm{substitution}w=-\ln \left(x\right),x=e^{-w}$$$$I=\underset{\mathrm{\infty }}{\stackrel{0}{\int }}\frac{{(-\mathrm{w})}^2}{1+{\left({\mathrm{e}}^{-\mathrm{w}}\right)}^2}(-{\mathrm{e}}^{-\mathrm{w}}\mathrm{dw})$$$$\mathrm{I}=\underset{0}{\stackrel{\mathrm{\infty }}{\int }}{\mathrm{w}}^2.\frac{{\mathrm{e}}^{-\mathrm{w}}}{1+{\mathrm{e}}^{-2\mathrm{w}}}\mathrm{dw}$$$$[\frac{{\mathrm{e}}^{-\mathrm{w}}}{1+{\mathrm{e}}^{-2\mathrm{w}}}=\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}{(-1)}^{\mathrm{n}-1}{\mathrm{e}}^{-(2\mathrm{n}+1)\mathrm{w}}]$$$$\mathrm{I}=\underset{\mathrm{n}=1}{\sum ^{\mathrm{\infty }}}{(-1)}^{\mathrm{n}}\underset{0}{\stackrel{\mathrm{\infty }}{\int }}{\left(\frac{\mathrm{t}}{2\mathrm{n}+1}\right)}^2{\mathrm{e}}^{-\mathrm{t}}\frac{\mathrm{dt}}{2\mathrm{n}+1};$$$$\mathrm{where}\mathrm{t}=(2\mathrm{n}+1)\mathrm{w}$$$$\mathrm{I}=\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^{\mathrm{n}}}{{(2\mathrm{n}+1)}^3}\underset{0}{\stackrel{\mathrm{\infty }}{\int }}{\mathrm{t}}^2{\mathrm{e}}^{-\mathrm{t}}\mathrm{dt}$$$$\mathrm{I}=\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^{\mathrm{n}}}{{(2\mathrm{n}+1)}^3}.2!=2\times \underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^{\mathrm{n}}}{{(2\mathrm{n}+1)}^3}$$$$\mathrm{I}=2\times \frac{{\pi }^3}{32}=\frac{{\pi }^3}{16}◼$$

Commented by  M±th+et+s last updated on 11/Jun/20

$$gotoQ.97369$$

Commented by bemath last updated on 13/Jun/20

$$\mathrm{greatt}$$

Answered by mathmax by abdo last updated on 11/Jun/20

$$\mathrm{I}={\int }_0^1\frac{{\ln }^2\mathrm{x}}{{\mathrm{x}}^2+1}\mathrm{dx}\Rightarrow \mathrm{I}={\int }_0^1{\ln }^2\left(\mathrm{x}\right)\left(\sum _{\mathrm{n}=0}^{\mathrm{\infty }}{(-1)}^{\mathrm{n}}{\mathrm{x}}^{2\mathrm{n}}\right)\mathrm{dx}$$$$=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}{(-1)}^{\mathrm{n}}{\int }_0^1{\ln }^2\mathrm{x}{\mathrm{x}}^{2\mathrm{n}}\mathrm{dx}\mathrm{let}{\mathrm{A}}_{\mathrm{n}}={\int }_0^1{\ln }^2\mathrm{x}{\mathrm{x}}^{2\mathrm{n}}\mathrm{dx}\mathrm{changement}\mathrm{lnx}=-\mathrm{t}$$$$\mathrm{give}{\mathrm{A}}_{\mathrm{n}}=-{\int }_0^{\mathrm{\infty }}{\mathrm{t}}^2{\left({\mathrm{e}}^{-\mathrm{t}}\right)}^{2\mathrm{n}}(-{\mathrm{e}}^{-\mathrm{t}})\mathrm{dt}$$$$={\int }_0^{\mathrm{\infty }}{\mathrm{t}}^2{\mathrm{e}}^{-(2\mathrm{n}+1)\mathrm{t}}\mathrm{dt}{=}_{(2\mathrm{n}+1)\mathrm{t}=\mathrm{u}}{\int }_0^{\mathrm{\infty }}\frac{{\mathrm{u}}^2}{{(2\mathrm{n}+1)}^2}{\mathrm{e}}^{-\mathrm{u}}\frac{\mathrm{du}}{(2\mathrm{n}+1)}$$$$=\frac{1}{{(2\mathrm{n}+1)}^3}{\int }_0^{\mathrm{\infty }}{\mathrm{u}}^2{\mathrm{e}}^{-\mathrm{u}}\mathrm{du}\mathrm{but}{\int }_0^{\mathrm{\infty }}{\mathrm{t}}^{\mathrm{x}-1}{\mathrm{e}}^{-\mathrm{t}}\mathrm{dt}=\mathrm{\Gamma }\left(\mathrm{x}\right)\Rightarrow {\int }_0^{\mathrm{\infty }}{\mathrm{u}}^2{\mathrm{e}}^{-\mathrm{u}}\mathrm{du}=\mathrm{\Gamma }\left(3\right)=2!=2$$$$\Rightarrow {\mathrm{A}}_{\mathrm{n}}=\frac{2}{{(2\mathrm{n}+1)}^3}\Rightarrow \mathrm{I}=2\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{{(-1)}^{\mathrm{n}}}{{(2\mathrm{n}+1)}^3}\mathrm{rest}\mathrm{to}\mathrm{calculate}\mathrm{this}\mathrm{serie}\mathrm{by}\mathrm{fourier}...$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com