Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 98098 by bobhans last updated on 11/Jun/20

what is the length of the chord cut off by y = 2x+1 from circle x^2 +y^2 =2

$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{cut} \\ $$$$\mathrm{off}\:\mathrm{by}\:\mathrm{y}\:=\:\mathrm{2x}+\mathrm{1}\:\mathrm{from}\:\mathrm{circle}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{2} \\ $$

Answered by john santu last updated on 11/Jun/20

Commented by john santu last updated on 11/Jun/20

A^⌢ B^⌢ = ∫_(−1) ^(0.2) (√(1+((dy/dx))^2 )) dx ⇔(d/dx) [ x^2 +y^2 = 2 ] 2x + 2yy ′ = 0 ; y′ = −(x/y) (y′)^2 = (x^2 /(2−x^2 )) . A^⌢ B^⌢ = ∫_(−1) ^(0.2) (√(1+(x^2 /(2−x^2 )))) dx = ∫_(−1) ^(0.2) (√(2/(2−x^2 ))) dx = (√2) ∫_(−1) ^(0.2) (dx/(√(2−x^2 ))) set x = (√2) sin t [ ∫ (((√2) cos t dt)/(√(2(1−sin^2 t)))) = sin^(−1) ((x/(√2))) ] then A^⌢ B^⌢ = (√2) [ sin^(−1) ((x/(√2))) ]_(−1) ^(0.2) = (√2) (sin^(−1) ((1/(5(√2))))+(π/4) )

$$\overset{\frown} {\mathrm{A}}\overset{\frown} {\mathrm{B}}\:=\:\underset{−\mathrm{1}} {\overset{\mathrm{0}.\mathrm{2}} {\int}}\:\sqrt{\mathrm{1}+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} }\:\mathrm{dx}\: \\ $$$$\Leftrightarrow\frac{\mathrm{d}}{\mathrm{dx}}\:\left[\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{2}\:\right] \\ $$$$\mathrm{2x}\:+\:\mathrm{2yy}\:'\:=\:\mathrm{0}\:;\:\mathrm{y}'\:=\:−\frac{\mathrm{x}}{\mathrm{y}} \\ $$$$\left(\mathrm{y}'\right)^{\mathrm{2}} \:=\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }\:. \\ $$$$\overset{\frown} {\mathrm{A}}\overset{\frown} {\mathrm{B}}\:=\:\underset{−\mathrm{1}} {\overset{\mathrm{0}.\mathrm{2}} {\int}}\:\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\: \\ $$$$=\:\underset{−\mathrm{1}} {\overset{\mathrm{0}.\mathrm{2}} {\int}}\:\sqrt{\frac{\mathrm{2}}{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:=\:\sqrt{\mathrm{2}}\:\underset{−\mathrm{1}} {\overset{\mathrm{0}.\mathrm{2}} {\int}}\:\frac{\mathrm{dx}}{\sqrt{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{set}\:\mathrm{x}\:=\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{t}\: \\ $$$$\left[\:\int\:\frac{\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{t}\:\mathrm{dt}}{\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{t}\right)}}\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\sqrt{\mathrm{2}}}\right)\:\right] \\ $$$$\mathrm{then}\:\overset{\frown} {\mathrm{A}}\overset{\frown} {\mathrm{B}}\:=\:\sqrt{\mathrm{2}}\:\left[\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\sqrt{\mathrm{2}}}\right)\:\right]_{−\mathrm{1}} ^{\mathrm{0}.\mathrm{2}} \\ $$$$=\:\sqrt{\mathrm{2}}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{5}\sqrt{\mathrm{2}}}\right)+\frac{\pi}{\mathrm{4}}\:\right) \\ $$

Answered by mr W last updated on 11/Jun/20

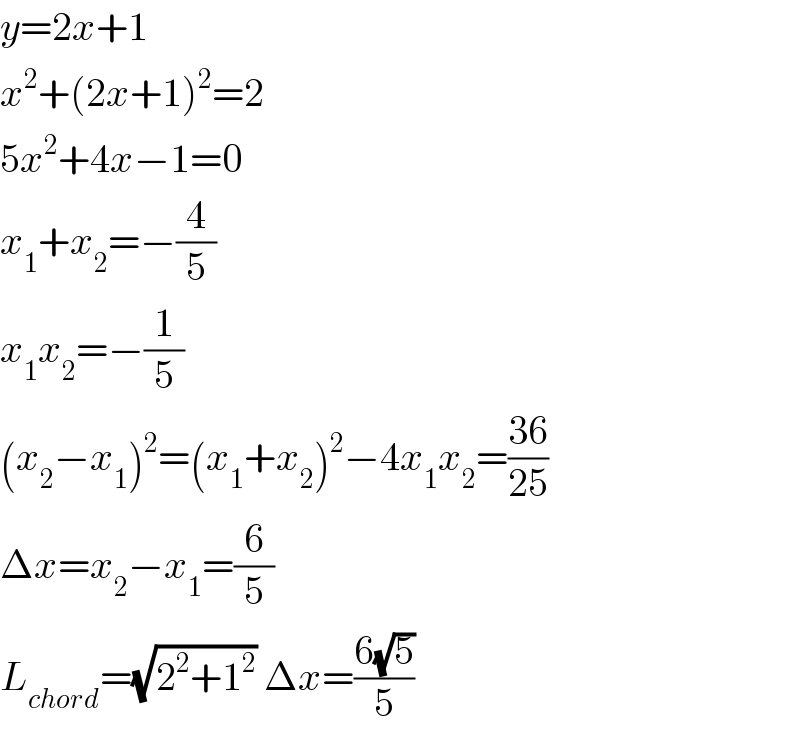
y=2x+1 x^2 +(2x+1)^2 =2 5x^2 +4x−1=0 x_1 +x_2 =−(4/5) x_1 x_2 =−(1/5) (x_2 −x_1 )^2 =(x_1 +x_2 )^2 −4x_1 x_2 =((36)/(25)) Δx=x_2 −x_1 =(6/5) L_(chord) =(√(2^2 +1^2 )) Δx=((6(√5))/5)

$${y}=\mathrm{2}{x}+\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} =\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{1}} {x}_{\mathrm{2}} =\frac{\mathrm{36}}{\mathrm{25}} \\ $$$$\Delta{x}={x}_{\mathrm{2}} −{x}_{\mathrm{1}} =\frac{\mathrm{6}}{\mathrm{5}} \\ $$$${L}_{{chord}} =\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }\:\Delta{x}=\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$

Commented by bobhans last updated on 11/Jun/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by 1549442205 last updated on 11/Jun/20

Intersection points of the line y=2x+1 and the circle x^2 +y^2 =2 have the cordinates be the roots of the system of equations: { ((y=2x+1(1))),((x^2 +y^2 =2(2))) :} Replace (1)into (2) we get x^2 +(2x+1)^2 =2 ⇔5x^2 +4x−1=0⇔x_A =−1,x_B =(1/5)⇒y_A =−1,y_B =(7/5).We get A(−1;−1),B((1/5);(7/5)) AB=(√((x_A −x_B )^2 +(y_A −y_B )^2 )) =(√(((6/5))^2 +(((12)/5))^2 )) =(√(((36+144)/(25)) )) =(√((180)/(25))) =((6(√5))/5) Thus,the length of the chord AB is ((6(√5))/5)

$$\mathrm{Intersection}\:\mathrm{points}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{2x}+\mathrm{1}\:\mathrm{and}\: \\ $$$$\mathrm{the}\:\mathrm{circle}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{2}\:\mathrm{have}\:\mathrm{the}\:\mathrm{cordinates} \\ $$$$\mathrm{be}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations}: \\ $$$$\begin{cases}{\mathrm{y}=\mathrm{2x}+\mathrm{1}\left(\mathrm{1}\right)}\\{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{2}\right)}\end{cases} \\ $$$$\mathrm{Replace}\:\left(\mathrm{1}\right)\mathrm{into}\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}^{\mathrm{2}} +\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\Leftrightarrow\mathrm{5x}^{\mathrm{2}} +\mathrm{4x}−\mathrm{1}=\mathrm{0}\Leftrightarrow\mathrm{x}_{\mathrm{A}} =−\mathrm{1},\mathrm{x}_{\mathrm{B}} =\frac{\mathrm{1}}{\mathrm{5}}\Rightarrow\mathrm{y}_{\mathrm{A}} =−\mathrm{1},\mathrm{y}_{\mathrm{B}} =\frac{\mathrm{7}}{\mathrm{5}}.\mathrm{We}\:\mathrm{get} \\ $$$$\mathrm{A}\left(−\mathrm{1};−\mathrm{1}\right),\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{5}};\frac{\mathrm{7}}{\mathrm{5}}\right) \\ $$$$\mathrm{AB}=\sqrt{\left(\mathrm{x}_{\mathrm{A}} −\mathrm{x}_{\mathrm{B}} \right)^{\mathrm{2}} +\left(\mathrm{y}_{\mathrm{A}} −\mathrm{y}_{\mathrm{B}} \right)^{\mathrm{2}} }\: \\ $$$$=\sqrt{\left(\frac{\mathrm{6}}{\mathrm{5}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{12}}{\mathrm{5}}\right)^{\mathrm{2}} }\:=\sqrt{\frac{\mathrm{36}+\mathrm{144}}{\mathrm{25}}\:}\:=\sqrt{\frac{\mathrm{180}}{\mathrm{25}}}\:=\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{AB}\:\mathrm{is}\:\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com