Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 98105 by mathmax by abdo last updated on 11/Jun/20

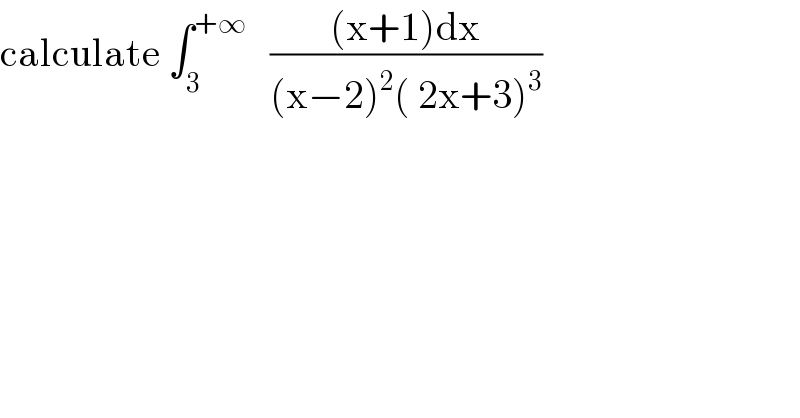
calculate ∫_3 ^(+∞) (((x+1)dx)/((x−2)^2 ( 2x+3)^3 ))

$$\mathrm{calculate}\:\int_{\mathrm{3}} ^{+\infty} \:\:\:\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \left(\:\mathrm{2x}+\mathrm{3}\right)^{\mathrm{3}} } \\ $$

Answered by MJS last updated on 11/Jun/20

∫((x+1)/((x−2)^2 (2x+3)^3 ))dx= [Ostrogradski] =−((44x^2 +55x+8)/(686(x−2)(2x+3)^2 ))−((11)/(343))∫(dx/((x−2)(2x+3)))= =−((44x^2 +55x+8)/(686(x−2)(2x+3)^2 ))+((11)/(2401))ln ∣((2x+3)/(x−2))∣ +C ∫_3 ^(+∞) ((x+1)/((x−2)^2 (2x+3)^3 ))dx=((569)/(55566))+((11)/(2401))(ln 2 −2ln 3)

$$\int\frac{{x}+\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{3}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=−\frac{\mathrm{44}{x}^{\mathrm{2}} +\mathrm{55}{x}+\mathrm{8}}{\mathrm{686}\left({x}−\mathrm{2}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} }−\frac{\mathrm{11}}{\mathrm{343}}\int\frac{{dx}}{\left({x}−\mathrm{2}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)}= \\ $$$$=−\frac{\mathrm{44}{x}^{\mathrm{2}} +\mathrm{55}{x}+\mathrm{8}}{\mathrm{686}\left({x}−\mathrm{2}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{11}}{\mathrm{2401}}\mathrm{ln}\:\mid\frac{\mathrm{2}{x}+\mathrm{3}}{{x}−\mathrm{2}}\mid\:+{C} \\ $$$$\underset{\mathrm{3}} {\overset{+\infty} {\int}}\frac{{x}+\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{3}} }{dx}=\frac{\mathrm{569}}{\mathrm{55566}}+\frac{\mathrm{11}}{\mathrm{2401}}\left(\mathrm{ln}\:\mathrm{2}\:−\mathrm{2ln}\:\mathrm{3}\right) \\ $$

Commented by mathmax by abdo last updated on 11/Jun/20

thank you sir MJS

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{MJS} \\ $$

Answered by mathmax by abdo last updated on 11/Jun/20

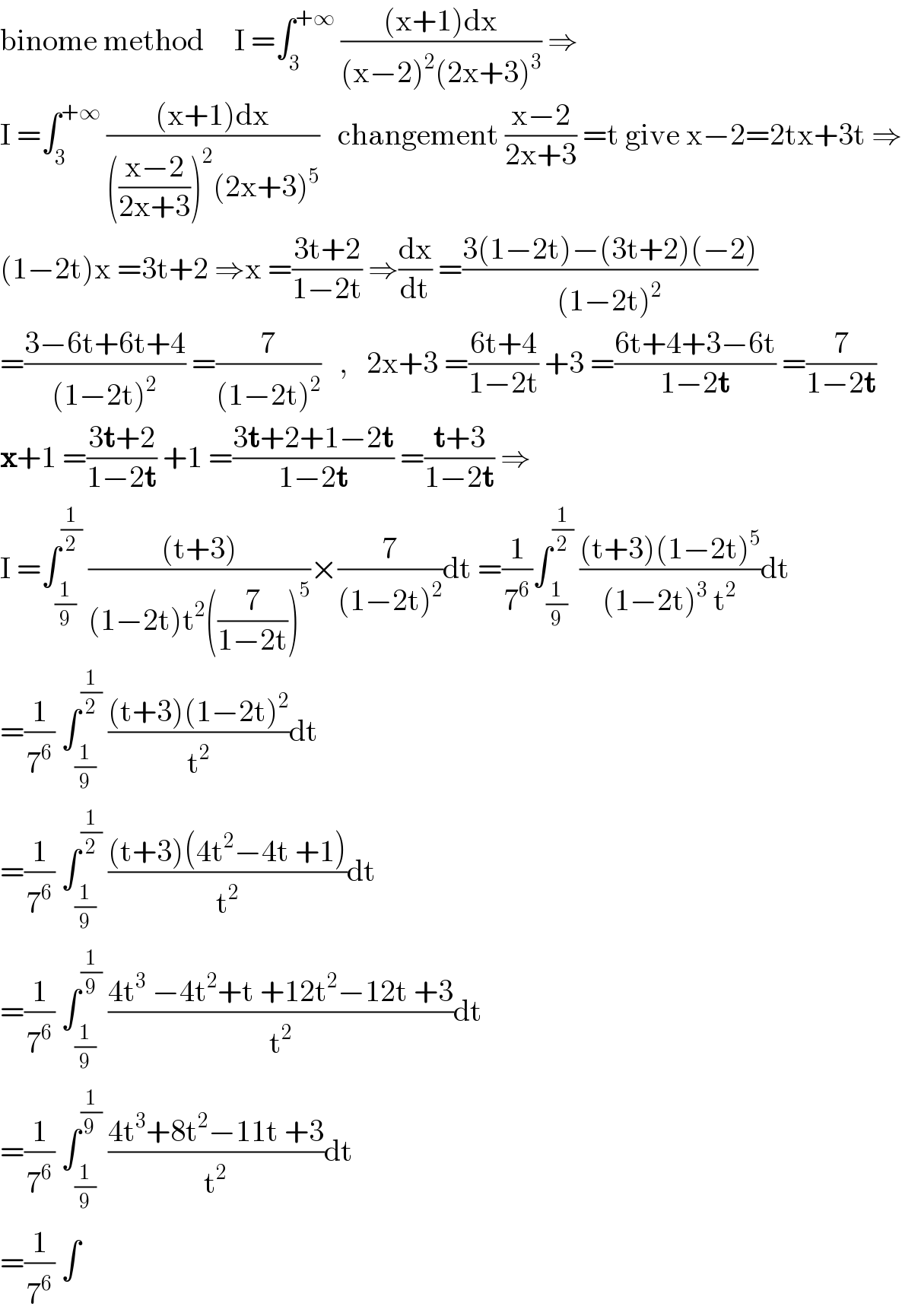
binome method I =∫_3 ^(+∞) (((x+1)dx)/((x−2)^2 (2x+3)^3 )) ⇒ I =∫_3 ^(+∞) (((x+1)dx)/((((x−2)/(2x+3)))^2 (2x+3)^5 )) changement ((x−2)/(2x+3)) =t give x−2=2tx+3t ⇒ (1−2t)x =3t+2 ⇒x =((3t+2)/(1−2t)) ⇒(dx/dt) =((3(1−2t)−(3t+2)(−2))/((1−2t)^2 )) =((3−6t+6t+4)/((1−2t)^2 )) =(7/((1−2t)^2 )) , 2x+3 =((6t+4)/(1−2t)) +3 =((6t+4+3−6t)/(1−2t)) =(7/(1−2t)) x+1 =((3t+2)/(1−2t)) +1 =((3t+2+1−2t)/(1−2t)) =((t+3)/(1−2t)) ⇒ I =∫_(1/9) ^(1/2) (((t+3))/((1−2t)t^2 ((7/(1−2t)))^5 ))×(7/((1−2t)^2 ))dt =(1/7^6 )∫_(1/9) ^(1/2) (((t+3)(1−2t)^5 )/((1−2t)^3 t^2 ))dt =(1/7^6 ) ∫_(1/9) ^(1/2) (((t+3)(1−2t)^2 )/t^2 )dt =(1/7^6 ) ∫_(1/9) ^(1/2) (((t+3)(4t^2 −4t +1))/t^2 )dt =(1/7^6 ) ∫_(1/9) ^(1/9) ((4t^3 −4t^2 +t +12t^2 −12t +3)/t^2 )dt =(1/7^6 ) ∫_(1/9) ^(1/(9 )) ((4t^3 +8t^2 −11t +3)/t^2 )dt =(1/7^6 ) ∫

$$\mathrm{binome}\:\mathrm{method}\:\:\:\:\:\mathrm{I}\:=\int_{\mathrm{3}} ^{+\infty} \:\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{3}} ^{+\infty} \:\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{dx}}{\left(\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2x}+\mathrm{3}}\right)^{\mathrm{2}} \left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{5}} }\:\:\:\mathrm{changement}\:\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2x}+\mathrm{3}}\:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}−\mathrm{2}=\mathrm{2tx}+\mathrm{3t}\:\Rightarrow \\ $$$$\left(\mathrm{1}−\mathrm{2t}\right)\mathrm{x}\:=\mathrm{3t}+\mathrm{2}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{3t}+\mathrm{2}}{\mathrm{1}−\mathrm{2t}}\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}\:=\frac{\mathrm{3}\left(\mathrm{1}−\mathrm{2t}\right)−\left(\mathrm{3t}+\mathrm{2}\right)\left(−\mathrm{2}\right)}{\left(\mathrm{1}−\mathrm{2t}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{3}−\mathrm{6t}+\mathrm{6t}+\mathrm{4}}{\left(\mathrm{1}−\mathrm{2t}\right)^{\mathrm{2}} }\:=\frac{\mathrm{7}}{\left(\mathrm{1}−\mathrm{2t}\right)^{\mathrm{2}} }\:\:\:,\:\:\:\mathrm{2x}+\mathrm{3}\:=\frac{\mathrm{6t}+\mathrm{4}}{\mathrm{1}−\mathrm{2t}}\:+\mathrm{3}\:=\frac{\mathrm{6t}+\mathrm{4}+\mathrm{3}−\mathrm{6t}}{\mathrm{1}−\mathrm{2}\boldsymbol{\mathrm{t}}}\:=\frac{\mathrm{7}}{\mathrm{1}−\mathrm{2}\boldsymbol{\mathrm{t}}} \\ $$$$\boldsymbol{\mathrm{x}}+\mathrm{1}\:=\frac{\mathrm{3}\boldsymbol{\mathrm{t}}+\mathrm{2}}{\mathrm{1}−\mathrm{2}\boldsymbol{\mathrm{t}}}\:+\mathrm{1}\:=\frac{\mathrm{3}\boldsymbol{\mathrm{t}}+\mathrm{2}+\mathrm{1}−\mathrm{2}\boldsymbol{\mathrm{t}}}{\mathrm{1}−\mathrm{2}\boldsymbol{\mathrm{t}}}\:=\frac{\boldsymbol{\mathrm{t}}+\mathrm{3}}{\mathrm{1}−\mathrm{2}\boldsymbol{\mathrm{t}}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\frac{\mathrm{1}}{\mathrm{9}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\left(\mathrm{t}+\mathrm{3}\right)}{\left(\mathrm{1}−\mathrm{2t}\right)\mathrm{t}^{\mathrm{2}} \left(\frac{\mathrm{7}}{\mathrm{1}−\mathrm{2t}}\right)^{\mathrm{5}} }×\frac{\mathrm{7}}{\left(\mathrm{1}−\mathrm{2t}\right)^{\mathrm{2}} }\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{6}} }\int_{\frac{\mathrm{1}}{\mathrm{9}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\left(\mathrm{t}+\mathrm{3}\right)\left(\mathrm{1}−\mathrm{2t}\right)^{\mathrm{5}} }{\left(\mathrm{1}−\mathrm{2t}\right)^{\mathrm{3}} \:\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{6}} }\:\int_{\frac{\mathrm{1}}{\mathrm{9}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\left(\mathrm{t}+\mathrm{3}\right)\left(\mathrm{1}−\mathrm{2t}\right)^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{6}} }\:\int_{\frac{\mathrm{1}}{\mathrm{9}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\left(\mathrm{t}+\mathrm{3}\right)\left(\mathrm{4t}^{\mathrm{2}} −\mathrm{4t}\:+\mathrm{1}\right)}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{6}} }\:\int_{\frac{\mathrm{1}}{\mathrm{9}}} ^{\frac{\mathrm{1}}{\mathrm{9}}} \:\frac{\mathrm{4t}^{\mathrm{3}} \:−\mathrm{4t}^{\mathrm{2}} +\mathrm{t}\:+\mathrm{12t}^{\mathrm{2}} −\mathrm{12t}\:+\mathrm{3}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{6}} }\:\int_{\frac{\mathrm{1}}{\mathrm{9}}} ^{\frac{\mathrm{1}}{\mathrm{9}\:}} \:\frac{\mathrm{4t}^{\mathrm{3}} +\mathrm{8t}^{\mathrm{2}} −\mathrm{11t}\:+\mathrm{3}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{6}} }\:\int \\ $$

Commented by mathmax by abdo last updated on 11/Jun/20

I =(1/7^6 ) { ∫_(1/9) ^(1/2) (4t +8−((11)/t) +(3/t^2 ))dt} =(1/7^6 )[ 2t^2 +8t −11ln∣t∣ −(3/t)]_(1/9) ^(1/2) =(1/7^6 )( (1/2) +4+11ln(2)−6 −2((1/9))^2 −8×(1/9) 11ln((1/9))+27) =...

$$\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{6}} }\:\left\{\:\int_{\frac{\mathrm{1}}{\mathrm{9}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\left(\mathrm{4t}\:+\mathrm{8}−\frac{\mathrm{11}}{\mathrm{t}}\:+\frac{\mathrm{3}}{\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{6}} }\left[\:\mathrm{2t}^{\mathrm{2}} \:+\mathrm{8t}\:−\mathrm{11ln}\mid\mathrm{t}\mid\:−\frac{\mathrm{3}}{\mathrm{t}}\right]_{\frac{\mathrm{1}}{\mathrm{9}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{6}} }\left(\:\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{4}+\mathrm{11ln}\left(\mathrm{2}\right)−\mathrm{6}\:−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{9}}\right)^{\mathrm{2}} \:−\mathrm{8}×\frac{\mathrm{1}}{\mathrm{9}}\:\mathrm{11ln}\left(\frac{\mathrm{1}}{\mathrm{9}}\right)+\mathrm{27}\right)\:=... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com