Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 98118 by abdomathmax last updated on 11/Jun/20

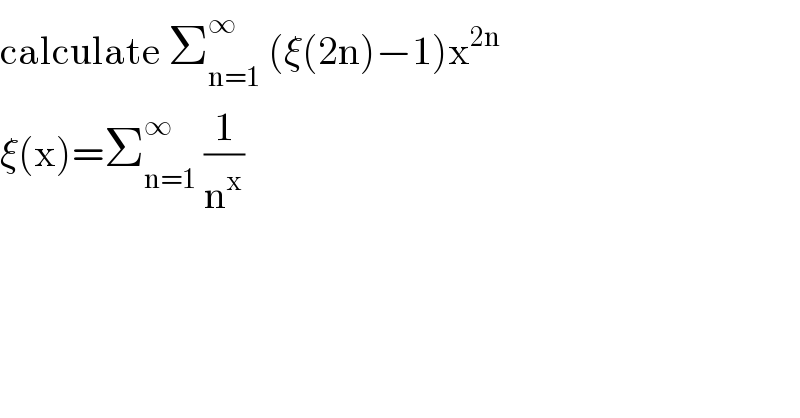
calculate Σ_(n=1) ^∞ (ξ(2n)−1)x^(2n) ξ(x)=Σ_(n=1) ^∞ (1/n^x )

$$\mathrm{calculate}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(\xi\left(\mathrm{2n}\right)−\mathrm{1}\right)\mathrm{x}^{\mathrm{2n}} \\ $$$$\xi\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{x}} } \\ $$

Answered by maths mind last updated on 11/Jun/20

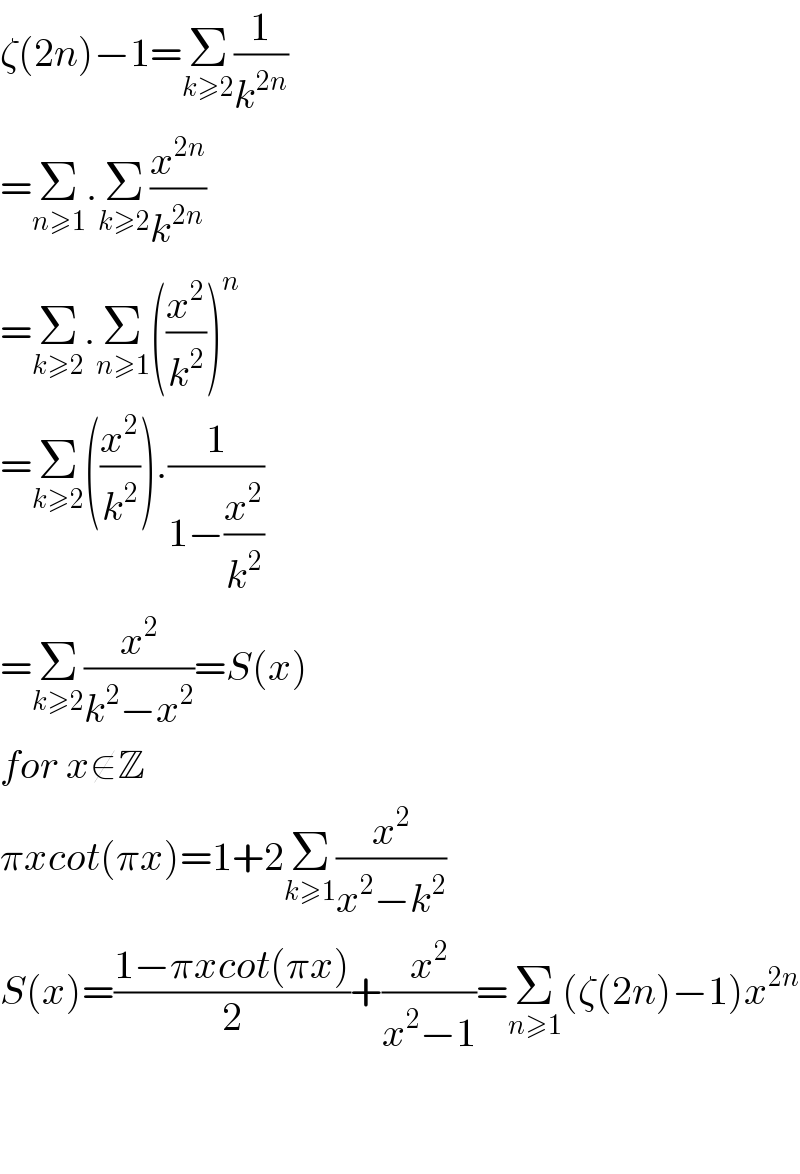
ζ(2n)−1=Σ_(k≥2) (1/k^(2n) ) =Σ_(n≥1) .Σ_(k≥2) (x^(2n) /k^(2n) ) =Σ_(k≥2) .Σ_(n≥1) ((x^2 /k^2 ))^n =Σ_(k≥2) ((x^2 /k^2 )).(1/(1−(x^2 /k^2 ))) =Σ_(k≥2) (x^2 /(k^2 −x^2 ))=S(x) for x∉Z πxcot(πx)=1+2Σ_(k≥1) (x^2 /(x^2 −k^2 )) S(x)=((1−πxcot(πx))/2)+(x^2 /(x^2 −1))=Σ_(n≥1) (ζ(2n)−1)x^(2n)

$$\zeta\left(\mathrm{2}{n}\right)−\mathrm{1}=\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{1}}{{k}^{\mathrm{2}{n}} } \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}.\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{{x}^{\mathrm{2}{n}} }{{k}^{\mathrm{2}{n}} } \\ $$$$=\underset{{k}\geqslant\mathrm{2}} {\sum}.\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{{x}^{\mathrm{2}} }{{k}^{\mathrm{2}} }\right)^{{n}} \\ $$$$=\underset{{k}\geqslant\mathrm{2}} {\sum}\left(\frac{{x}^{\mathrm{2}} }{{k}^{\mathrm{2}} }\right).\frac{\mathrm{1}}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{k}^{\mathrm{2}} }} \\ $$$$=\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{{x}^{\mathrm{2}} }{{k}^{\mathrm{2}} −{x}^{\mathrm{2}} }={S}\left({x}\right) \\ $$$${for}\:{x}\notin\mathbb{Z} \\ $$$$\pi{xcot}\left(\pi{x}\right)=\mathrm{1}+\mathrm{2}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −{k}^{\mathrm{2}} } \\ $$$${S}\left({x}\right)=\frac{\mathrm{1}−\pi{xcot}\left(\pi{x}\right)}{\mathrm{2}}+\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{1}}=\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\zeta\left(\mathrm{2}{n}\right)−\mathrm{1}\right){x}^{\mathrm{2}{n}} \\ $$$$ \\ $$$$ \\ $$

Commented by maths mind last updated on 11/Jun/20

x∈]1,2[

$$\left.{x}\in\right]\mathrm{1},\mathrm{2}\left[\right. \\ $$

Commented by mathmax by abdo last updated on 11/Jun/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com