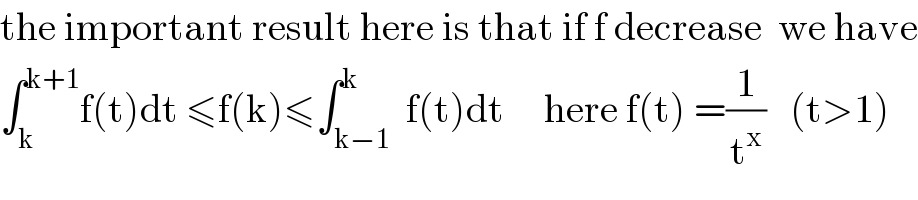let ξ(x) =Σ_(n=1) ^∞ (1/n^x ) calculate lim


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 98189 by abdomathmax last updated on 12/Jun/20

$let ξ (x) = \sum_{n = 1}^{\infty} \frac{1}{n^{x}}$ $calculate \lim_{x \to 1^{+}} (x - 1) ξ (x)$
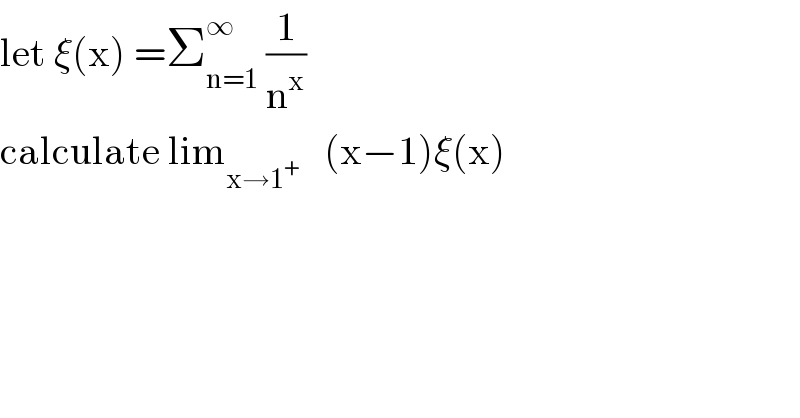
	Answered by mathmax by abdo last updated on 12/Jun/20
	$the function t→(1/t^x ) is decreazing on ]1,+∞[ so Σ_(k=2) ^n ∫_k ^(k+1) (dt/t^x ) ≤ Σ_(k=2) ^n (1/k^x ) ≤Σ_(k=2) ^n ∫_(k−1) ^k (dt/t^x ) ⇒ ∫_2 ^(n+1) (dt/t^x ) ≤ ξ_n (x) ≤∫_1 ^n (dt/t^x ) we have ∫_2 ^(n+1) (dt/t^x ) =∫_2 ^(n+1) t^(−x) dt =[(1/(1−x))t^(−x+1) ]_2 ^(n+1) =(1/(1−x)){ (1/((n+1)^(x−1) ))−(1/2^(x−1) )} =(1/((x−1))){(1/2^(x−1) )−(1/((n+1)^(x−1) ))} ∫_1 ^n t^(−x) dt =[(1/(−x+1)) t^(−x+1) ]_1 ^n =(1/(1−x))[ (1/t^(x−1) )]_1 ^n =(1/(1−x)){(1/n^(x−1) )−1} =(1/(x−1)){1−(1/n^(x−1) )} ⇒ (1/(x−1)){(1/2^(x−1) )−(1/((n+1)^(x−1) ))} ≤ Σ_(k=1) ^n (1/k^x )−1 ≤(1/(x−1)){1−(1/n^(x−1) )} ⇒ ∀x>1 (1/2^(x−1) ) −(1/((n+1)^(x−1) )) ≤(x−1)ξ_n (x)−(x−1)≤1−(1/n^(x−1) ) ⇒ ⇒(1/2^(x−1) ) ≤ (x−1)ξ(x)−(x−1)≤ 1 ⇒lim_(x→1^+ ) (1/2^(x−1) ) ≤lim_(x→1^+ ) (x−1)ξ(x)≤1 ⇒lim_(x→1^+ ) (x−1)ξ(x) =1$
	$the function t \to \frac{1}{t^{x}} is decreazing on] 1, + \infty [so$ $\sum_{k = 2}^{n} \int_{k}^{k + 1} \frac{dt}{t^{x}} ⩽ \sum_{k = 2}^{n} \frac{1}{k^{x}} ⩽ \sum_{k = 2}^{n} \int_{k - 1}^{k} \frac{dt}{t^{x}} \Rightarrow$ $\int_{2}^{n + 1} \frac{dt}{t^{x}} ⩽ ξ_{n} (x) ⩽ \int_{1}^{n} \frac{dt}{t^{x}} we have \int_{2}^{n + 1} \frac{dt}{t^{x}} = \int_{2}^{n + 1} t^{- x} dt = {[\frac{1}{1 - x} t^{- x + 1}]}_{2}^{n + 1}$ $= \frac{1}{1 - x} {\frac{1}{{(n + 1)}^{x - 1}} - \frac{1}{2^{x - 1}}} = \frac{1}{(x - 1)} {\frac{1}{2^{x - 1}} - \frac{1}{{(n + 1)}^{x - 1}}}$ $\int_{1}^{n} t^{- x} dt = {[\frac{1}{- x + 1} t^{- x + 1}]}_{1}^{n} = \frac{1}{1 - x} {[\frac{1}{t^{x - 1}}]}_{1}^{n} = \frac{1}{1 - x} {\frac{1}{n^{x - 1}} - 1}$ $= \frac{1}{x - 1} {1 - \frac{1}{n^{x - 1}}} \Rightarrow \frac{1}{x - 1} {\frac{1}{2^{x - 1}} - \frac{1}{{(n + 1)}^{x - 1}}} ⩽ \sum_{k = 1}^{n} \frac{1}{k^{x}} - 1 ⩽ \frac{1}{x - 1} {1 - \frac{1}{n^{x - 1}}} \Rightarrow$ $\forall x > 1 \frac{1}{2^{x - 1}} - \frac{1}{{(n + 1)}^{x - 1}} ⩽ (x - 1) ξ_{n} (x) - (x - 1) ⩽ 1 - \frac{1}{n^{x - 1}} \Rightarrow$ $\Rightarrow \frac{1}{2^{x - 1}} ⩽ (x - 1) ξ (x) - (x - 1) ⩽ 1 \Rightarrow \lim_{x \to 1^{+}} \frac{1}{2^{x - 1}} ⩽ \lim_{x \to 1^{+}} (x - 1) ξ (x) ⩽ 1$ $\Rightarrow \lim_{x \to 1^{+}} (x - 1) ξ (x) = 1$
	Commented by mathmax by abdo last updated on 12/Jun/20

	$the important result here is that if f decrease we have$ $\int_{k}^{k + 1} f (t) dt ⩽ f (k) ⩽ \int_{k - 1}^{k} f (t) dt here f (t) = \frac{1}{t^{x}} (t > 1)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum