for what value of :{x∣ 0<x<2𝛑}: 4cosec^2 x−9=cotx


Question and Answers Forum

All Questions Topic List
Trigonometry Questions
Previous in All Question Next in All Question
Previous in Trigonometry Next in Trigonometry
Question Number 98191 by behi83417@gmail.com last updated on 12/Jun/20
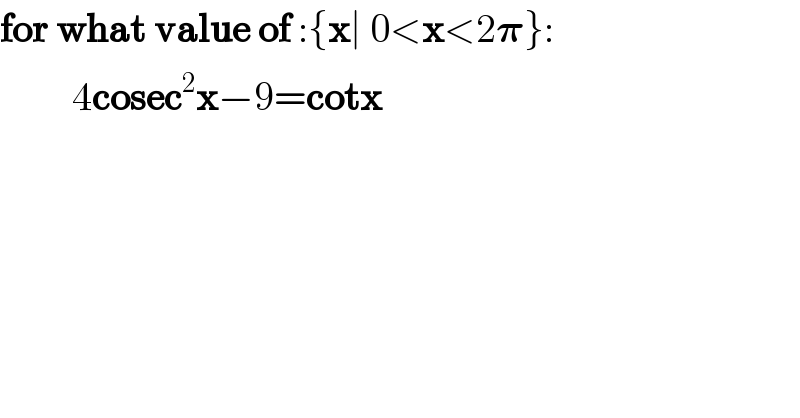
$for what value of :{x∣ 0<x<2𝛑}: 4cosec^2 x−9=cotx$
$for what value of : {x ∣ 0 < x < 2 π} :$ $4 {cosec}^{2} x - 9 = cotx$
	Answered by MJS last updated on 12/Jun/20

	${4 cosec}^{2} x - 9 = \cot x$ ${9 \sin}^{2} x + \sin x \cos x - 4 = 0$ $9 \cos 2 x - \sin 2 x - 1 = 0$ $x = \arctan t$ $- \frac{10 t^{2} + 2 t - 8}{t^{2} + 1} = 0$ $t^{2} + \frac{1}{5} t - \frac{4}{5} = 0$ $t_{1} = - 1; t_{2} = \frac{4}{5}$ $\Rightarrow$ $x_{1.1} = \frac{3 π}{4}; x_{1.2} = \frac{7 π}{4}; x_{2.1} = \arctan \frac{4}{5}; x_{2.2} = π + \arctan \frac{4}{5}$
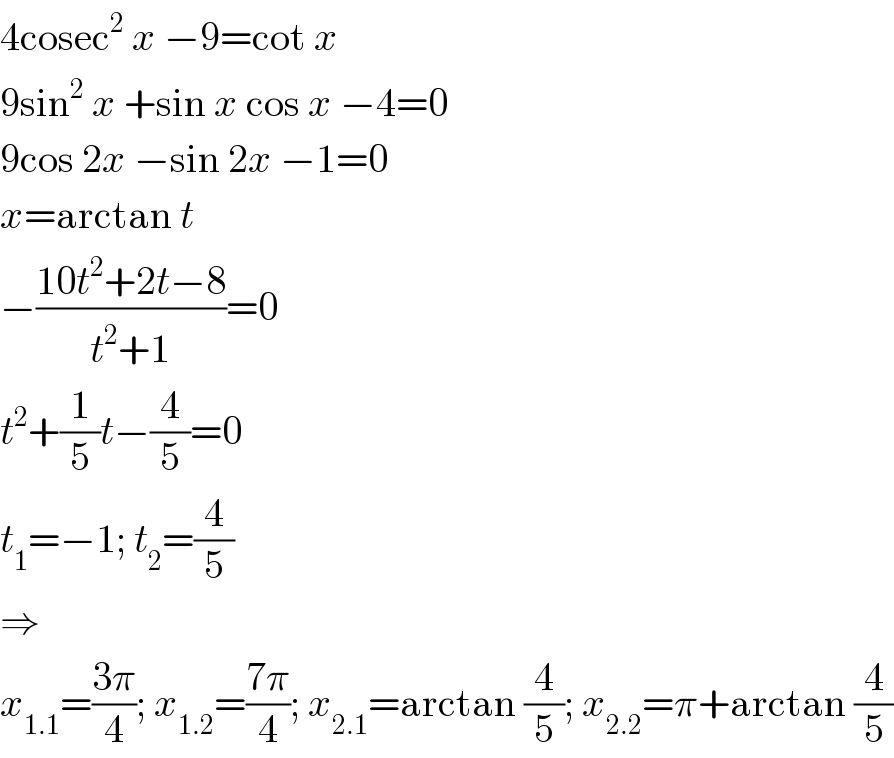
	Answered by 1549442205 last updated on 12/Jun/20
	$we have (4/(sin^2 x))−9=((cosx)/(sinx))⇔4(1+cot^2 x)−9=cotx 4cot^2 x−cotx−5=0⇔(cotx+1)(4cotx−5)=0 a/cotx+1=0⇔cot x=−1=cot((3π)/4)⇒x∈{((3π)/4);((7π)/4)} a/4cotx−5=0⇔cotx=(5/4)⇔tanx=(4/5) ⇒x∈{arctan(4/5);arctan(4/5)+π} Thus,the roots in interval [0;2π] of given equation are:x∈{((3π)/4);((7π)/4);arctan(4/5);arctan(4/5)+π}$
	$we have \frac{4}{\sin^{2} x} - 9 = \frac{cosx}{sinx} \Leftrightarrow 4 (1 + \cot^{2} x) - 9 = cotx$ ${4 \cot}^{2} x - cotx - 5 = 0 \Leftrightarrow (cotx + 1) (4 cotx - 5) = 0$ $a / cotx + 1 = 0 \Leftrightarrow \cot x = - 1 = \cot \frac{3 π}{4} \Rightarrow x \in {\frac{3 π}{4}; \frac{7 π}{4}}$ $a / 4 cotx - 5 = 0 \Leftrightarrow cotx = \frac{5}{4} \Leftrightarrow tanx = \frac{4}{5}$ $\Rightarrow x \in {\arctan \frac{4}{5}; \arctan \frac{4}{5} + π}$ $Thus, the roots in interval [0; 2 π] of$ $given equation are : x \in {\frac{3 π}{4}; \frac{7 π}{4}; \arctan \frac{4}{5}; \arctan \frac{4}{5} + π}$
	Commented bybehi83417@gmail.com last updated on 12/Jun/20

	$thank you very much sir .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum