
Question and Answers Forum
Question Number 98244 by ~blr237~ last updated on 12/Jun/20
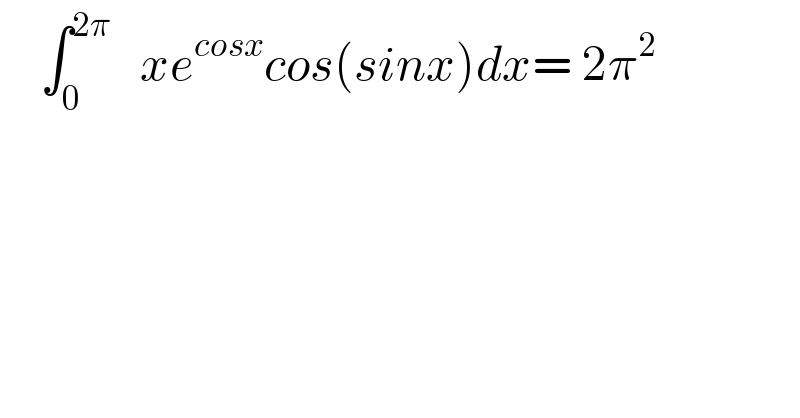
Answered by maths mind last updated on 15/Jun/20
![e^(cos(x)+isin(x)) =e^(cos(x)) (cos(sin(x))+isin(sin(x))) ∫_0 ^(2π) xe^(cos(x)+isin(x)) dx =∫_0 ^(2π) xe^e^(ix) dx =∫_0 ^(2π) Σ_(k≥0) x.(e^(ikx) /(k!)) =Σ_(k≥0) (1/(k!))∫_0 ^(2π) xe^(ikx) dx ∫_0 ^(2π) xe^(ikx) dx=[x(e^(ikx) /(ik))]−∫(e^(ik) /(ik))dx =((2π)/(ik)) ,k≠0 if k=0 ∫_0 ^(2π) xdx=2π^2 Re{∫_0 ^(2π) xe^e^(ix) dx}=∫_0 ^(2π) xe^(cos(x)) cos(sin(x))dx =Re[2π^2 +Σ_(k≥1) ((2π)/(ik.k!))] =2π^2 Σ(1/(kk!))=∫(e^x /x)dx=Σ_(k≥0) (x^k /(kk!)) ⇒∫xe^(cos(x)) sin(sin(x))dx=−2πE_i (1)](Q98674.png)
| ||
Question and Answers Forum | ||
Question Number 98244 by ~blr237~ last updated on 12/Jun/20 | ||
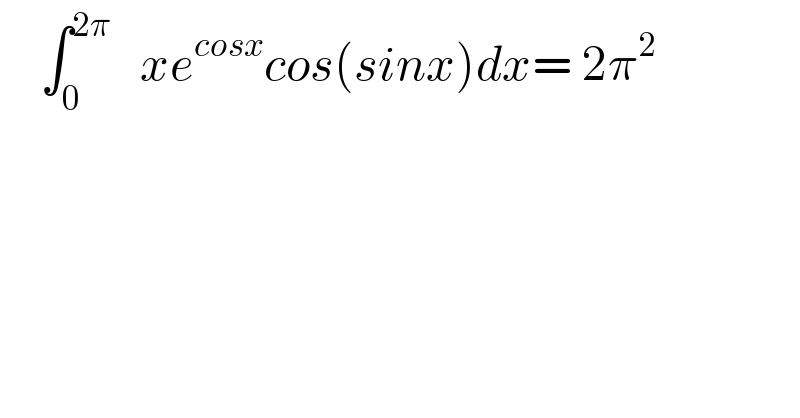 | ||
Answered by maths mind last updated on 15/Jun/20 | ||
![e^(cos(x)+isin(x)) =e^(cos(x)) (cos(sin(x))+isin(sin(x))) ∫_0 ^(2π) xe^(cos(x)+isin(x)) dx =∫_0 ^(2π) xe^e^(ix) dx =∫_0 ^(2π) Σ_(k≥0) x.(e^(ikx) /(k!)) =Σ_(k≥0) (1/(k!))∫_0 ^(2π) xe^(ikx) dx ∫_0 ^(2π) xe^(ikx) dx=[x(e^(ikx) /(ik))]−∫(e^(ik) /(ik))dx =((2π)/(ik)) ,k≠0 if k=0 ∫_0 ^(2π) xdx=2π^2 Re{∫_0 ^(2π) xe^e^(ix) dx}=∫_0 ^(2π) xe^(cos(x)) cos(sin(x))dx =Re[2π^2 +Σ_(k≥1) ((2π)/(ik.k!))] =2π^2 Σ(1/(kk!))=∫(e^x /x)dx=Σ_(k≥0) (x^k /(kk!)) ⇒∫xe^(cos(x)) sin(sin(x))dx=−2πE_i (1)](Q98674.png) | ||
| ||