∫_0 ^∞ ((log(x))/((√x)(x+1)^2 ))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 98256 by M±th+et+s last updated on 12/Jun/20

$\int_{0}^{\infty} \frac{l o g (x)}{\sqrt{x} {(x + 1)}^{2}} d x$
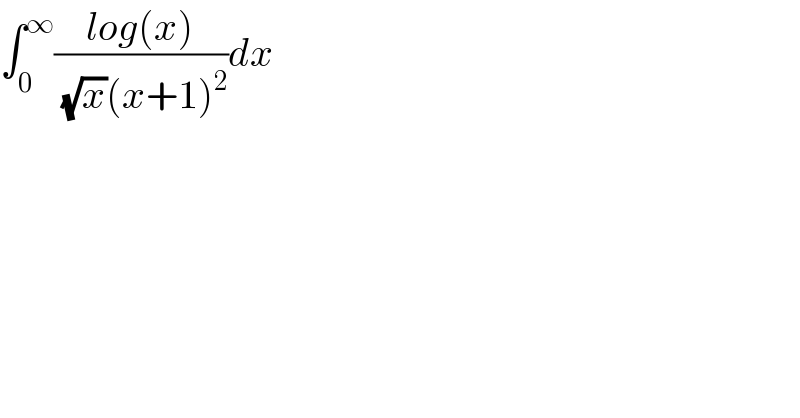
	Answered by mathmax by abdo last updated on 12/Jun/20
	$A =∫_0 ^∞ ((ln(x))/((√x)(x+1)^2 ))dx changement (√x)=t give x=t^2 ⇒ A =∫_0 ^∞ ((ln(t^2 ))/(t(t^2 +1)^2 )) (2t)dt =4 ∫_0 ^∞ ((ln(t))/((1+t^2 )^2 ))dt A =4{ ∫_0 ^1 ((ln(t))/((1+t^2 )^2 ))dt +∫_1 ^(+∞) ((lnt)/((1+t^2 )^2 ))dt(→t=(1/u))} =4{ ∫_0 ^1 ((ln(t))/((1+t^2 )^2 ))dt −∫_0 ^1 ((−lnu)/((1+(1/u^2 ))^2 ))(−(du/u^2 ))} =4{ ∫_0 ^1 ((ln(t))/((1+t^2 )^2 ))dt−∫_0 ^1 ((ln(u)u^2 )/((1+u^2 )^2 ))} =4 ∫_0 ^1 (((1−t^2 )lnt)/((1+t^2 )^2 )) dt we have (1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n ⇒−(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒ (1/((1+u)^2 )) =−Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒(1/((1+t^2 )^2 )) =−Σ_(n=1) ^∞ n(−1)^n t^(2n−2) ⇒ A =−4 ∫_0 ^1 (1−t^2 )ln(t)(Σ_(n=1) ^∞ n(−1)^n t^(2n−2) )dt =4 Σ_(n=1) ^∞ n(−1)^n ∫_0 ^1 (t^2 −1)t^(2n−2) ln(t)dt =4 Σ_(n=1) ^∞ n(−1)^n w_n W_n =∫_0 ^1 (t^(2n) −t^(2n−2) )ln(t)dt by parts W_n =[((t^(2n+1) /(2n+1)) −(t^(2n−1) /(2n−1)))ln(t)]_0 ^1 −∫_0 ^1 ((t^(2n+1) /(2n+1))−(t^(2n−1) /(2n−1)))(dt/t) =−(1/((2n+1)^2 )) +(1/((2n−1)^2 )) ⇒ A =4 Σ_(n=1) ^∞ n(−1)^n ((1/((2n−1)^2 ))−(1/((2n+1)^2 ))) =4 Σ_(n=1) ^∞ (−1)^n (n/((2n−1)^2 )) −4 Σ_(n=1) ^∞ (−1)^n (n/((2n+1)^2 )) Σ_(n=1) ^∞ ((n(−1)^n )/((2n−1)^2 )) =_(n=p+1) Σ_(p=0) ^∞ (((p+1)(−1)^(p+1) )/((2p+1)^2 )) =−1 −Σ_(n=1) ^∞ (((n+1)(−1)^n )/((2n+1)^2 )) =−1−Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) −Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) ⇒ A =−4−4Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) −4 Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 ))−4 Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) =−4 −4 Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) −8 Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) =k−1 (k catalan constsnt) Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) =(1/2)Σ_(n=1) ^∞ (((2n+1−1)(−1)^n )/((2n+1)^2 )) =(1/2) Σ_(n=1) ^∞ (((−1)^n )/((2n+1)))−(1/2)Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) =(1/2)((π/4)−1)−(1/2)(k−1) ⇒ A =−4 −4(k−1)−8{(π/8)−(1/2) −(1/2)(k−1)} =−4 −4(k−1)−π +4 +4(k−1) =−π ⇒ A =−π$
	$A = \int_{0}^{\infty} \frac{\ln (x)}{\sqrt{x} {(x + 1)}^{2}} dx changement \sqrt{x} = t give x = t^{2} \Rightarrow$ $A = \int_{0}^{\infty} \frac{\ln (t^{2})}{t {(t^{2} + 1)}^{2}} (2 t) dt = 4 \int_{0}^{\infty} \frac{\ln (t)}{{(1 + t^{2})}^{2}} dt$ $A = 4 {\int_{0}^{1} \frac{\ln (t)}{{(1 + t^{2})}^{2}} dt + \int_{1}^{+ \infty} \frac{lnt}{{(1 + t^{2})}^{2}} dt (\to t = \frac{1}{u})}$ $= 4 {\int_{0}^{1} \frac{\ln (t)}{{(1 + t^{2})}^{2}} dt - \int_{0}^{1} \frac{- lnu}{{(1 + \frac{1}{u^{2}})}^{2}} (- \frac{du}{u^{2}})}$ $= 4 {\int_{0}^{1} \frac{\ln (t)}{{(1 + t^{2})}^{2}} dt - \int_{0}^{1} \frac{\ln (u) u^{2}}{{(1 + u^{2})}^{2}}} = 4 \int_{0}^{1} \frac{(1 - t^{2}) lnt}{{(1 + t^{2})}^{2}} dt$ $we have \frac{1}{1 + u} = \sum_{n = 0}^{\infty} {(- 1)}^{n} u^{n} \Rightarrow - \frac{1}{{(1 + u)}^{2}} = \sum_{n = 1}^{\infty} n {(- 1)}^{n} u^{n - 1} \Rightarrow$ $\frac{1}{{(1 + u)}^{2}} = - \sum_{n = 1}^{\infty} n {(- 1)}^{n} u^{n - 1} \Rightarrow \frac{1}{{(1 + t^{2})}^{2}} = - \sum_{n = 1}^{\infty} n {(- 1)}^{n} t^{2 n - 2} \Rightarrow$ $A = - 4 \int_{0}^{1} (1 - t^{2}) \ln (t) (\sum_{n = 1}^{\infty} n {(- 1)}^{n} t^{2 n - 2}) dt$ $= 4 \sum_{n = 1}^{\infty} n {(- 1)}^{n} \int_{0}^{1} (t^{2} - 1) t^{2 n - 2} \ln (t) dt = 4 \sum_{n = 1}^{\infty} n {(- 1)}^{n} w_{n}$ $W_{n} = \int_{0}^{1} (t^{2 n} - t^{2 n - 2}) \ln (t) dt by parts$ $W_{n} = {[(\frac{t^{2 n + 1}}{2 n + 1} - \frac{t^{2 n - 1}}{2 n - 1}) \ln (t)]}_{0}^{1} - \int_{0}^{1} (\frac{t^{2 n + 1}}{2 n + 1} - \frac{t^{2 n - 1}}{2 n - 1}) \frac{dt}{t}$ $= - \frac{1}{{(2 n + 1)}^{2}} + \frac{1}{{(2 n - 1)}^{2}} \Rightarrow A = 4 \sum_{n = 1}^{\infty} n {(- 1)}^{n} (\frac{1}{{(2 n - 1)}^{2}} - \frac{1}{{(2 n + 1)}^{2}})$ $= 4 \sum_{n = 1}^{\infty} {(- 1)}^{n} \frac{n}{{(2 n - 1)}^{2}} - 4 \sum_{n = 1}^{\infty} {(- 1)}^{n} \frac{n}{{(2 n + 1)}^{2}}$ $\sum_{n = 1}^{\infty} \frac{n {(- 1)}^{n}}{{(2 n - 1)}^{2}} =_{n = p + 1} \sum_{p = 0}^{\infty} \frac{(p + 1) {(- 1)}^{p + 1}}{{(2 p + 1)}^{2}} = - 1 - \sum_{n = 1}^{\infty} \frac{(n + 1) {(- 1)}^{n}}{{(2 n + 1)}^{2}}$ $= - 1 - \sum_{n = 1}^{\infty} \frac{n {(- 1)}^{n}}{{(2 n + 1)}^{2}} - \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{{(2 n + 1)}^{2}} \Rightarrow$ $A = - 4 - 4 \sum_{n = 1}^{\infty} \frac{n {(- 1)}^{n}}{{(2 n + 1)}^{2}} - 4 \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{{(2 n + 1)}^{2}} - 4 \sum_{n = 1}^{\infty} \frac{n {(- 1)}^{n}}{{(2 n + 1)}^{2}}$ $= - 4 - 4 \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{{(2 n + 1)}^{2}} - 8 \sum_{n = 1}^{\infty} \frac{n {(- 1)}^{n}}{{(2 n + 1)}^{2}}$ $\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{{(2 n + 1)}^{2}} = k - 1 (k catalan constsnt)$ $\sum_{n = 1}^{\infty} \frac{n {(- 1)}^{n}}{{(2 n + 1)}^{2}} = \frac{1}{2} \sum_{n = 1}^{\infty} \frac{(2 n + 1 - 1) {(- 1)}^{n}}{{(2 n + 1)}^{2}} = \frac{1}{2} \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{(2 n + 1)} - \frac{1}{2} \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{{(2 n + 1)}^{2}}$ $= \frac{1}{2} (\frac{π}{4} - 1) - \frac{1}{2} (k - 1) \Rightarrow$ $A = - 4 - 4 (k - 1) - 8 {\frac{π}{8} - \frac{1}{2} - \frac{1}{2} (k - 1)}$ $= - 4 - 4 (k - 1) - π + 4 + 4 (k - 1) = - π \Rightarrow A = - π$
	Commented by M±th+et+s last updated on 12/Jun/20

	$w e l l d o n e .$ $c o r r e c t s o l u t i o n$
	Answered by maths mind last updated on 13/Jun/20

	$= \int_{0}^{+ \infty} \frac{2 l o g (t)}{t {(t^{2} + 1)}^{2}} . 2 t d t = 4 \int_{0} \frac{l o g (t)}{{(t^{2} + 1)}^{2}}$ $\Leftrightarrow 4 \int_{0}^{\frac{π}{2}} l o g (t g (z)) {c o s}^{2} (z)$ $= 4 \int_{0}^{\frac{π}{2}} l o g (s i n (z)) {c o s}^{2} (z) - l o g (c o s (z)) {c o s}^{2} (z) d z . . . 1$ $2 \int_{0}^{\frac{π}{2}} {s i n}^{2 x - 1} (t) {c o s}^{2 y - 1} (t) d t = β (x, y)$ $1 = \partial_{x} β (\frac{1}{2}, \frac{3}{2}) - \partial_{y} β (\frac{1}{2}, \frac{3}{2}) = β (\frac{1}{2}, \frac{3}{2}) (Ψ (\frac{1}{2}) - Ψ (\frac{3}{2}))$ $= β (\frac{1}{2}, \frac{3}{2}) (Ψ (\frac{1}{2}) - Ψ (\frac{1}{2}) - 2)$ $= - 2 . \frac{Γ (\frac{1}{2}) Γ (\frac{3}{2})}{Γ (2)} = - 2 Γ (\frac{1}{2}) . 2^{- 1} . \sqrt{π} . Γ (2) = - π$ $=$
	Commented by maths mind last updated on 13/Jun/20

	$i u s e d Γ (z) Γ (z + \frac{1}{2}) = 2^{1 - 2 z} \sqrt{π} . Γ (z)$ $f o r Γ (\frac{3}{2}), z = \frac{1}{2}, Γ (\frac{1}{2}) = \sqrt{π}$
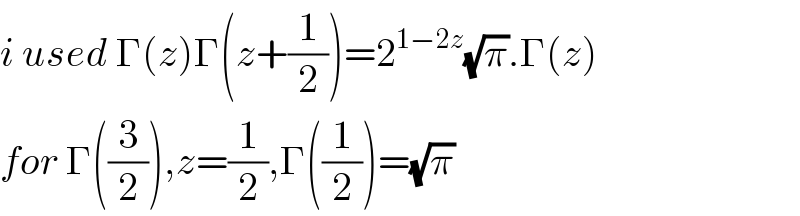
	Commented by M±th+et+s last updated on 13/Jun/20

	$v e r y n i c e s i r t h a n x$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum