Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 98267 by  M±th+et+s last updated on 12/Jun/20

∀ a,b>0 , a^2 +b^2 =1 prove that ((1/a)+(1/b))((b/(a^2 +1))+(a/(b^2 +1)))≥(8/3)

$$\forall\:{a},{b}>\mathrm{0}\:,\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$ $${prove}\:{that} \\ $$ $$\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right)\left(\frac{{b}}{{a}^{\mathrm{2}} +\mathrm{1}}+\frac{{a}}{{b}^{\mathrm{2}} +\mathrm{1}}\right)\geqslant\frac{\mathrm{8}}{\mathrm{3}} \\ $$

Answered by maths mind last updated on 13/Jun/20

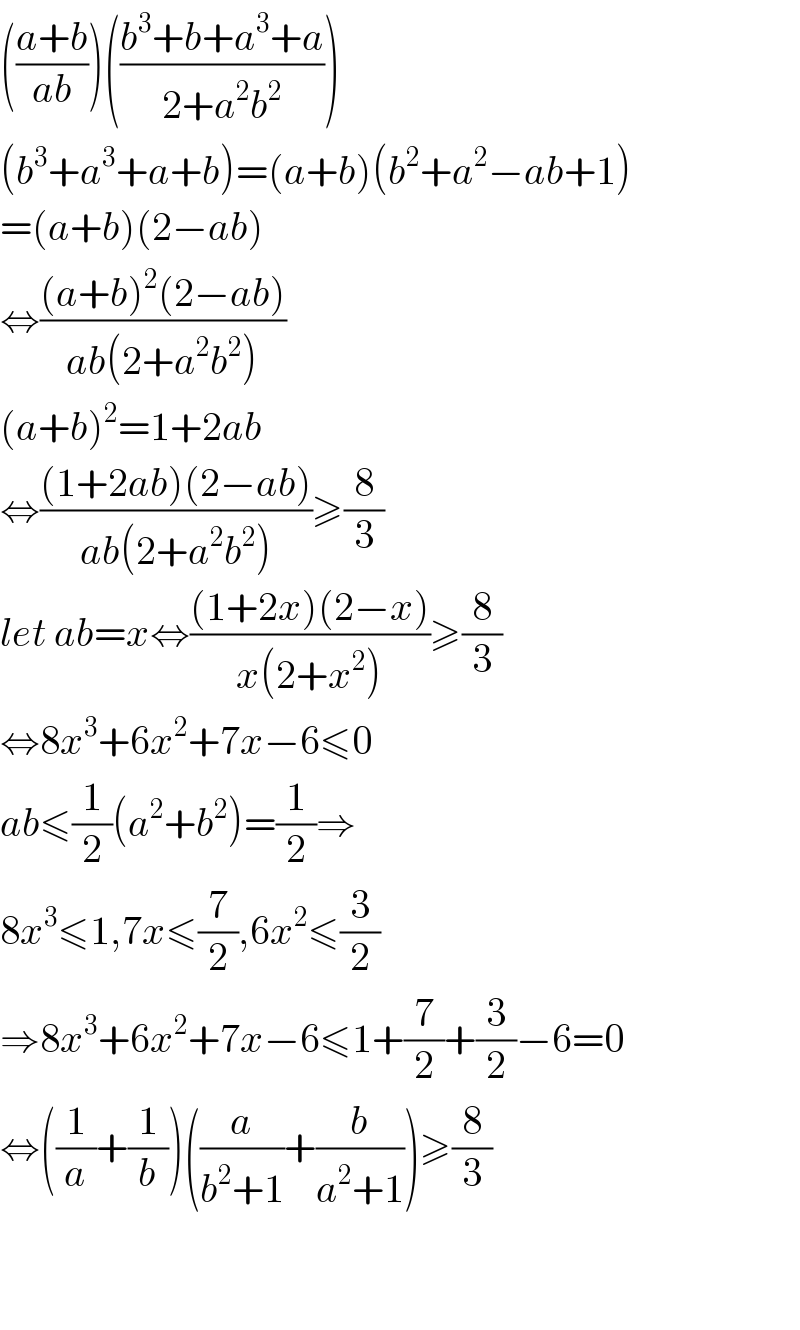
(((a+b)/(ab)))(((b^3 +b+a^3 +a)/(2+a^2 b^2 ))) (b^3 +a^3 +a+b)=(a+b)(b^2 +a^2 −ab+1) =(a+b)(2−ab) ⇔(((a+b)^2 (2−ab))/(ab(2+a^2 b^2 ))) (a+b)^2 =1+2ab ⇔(((1+2ab)(2−ab))/(ab(2+a^2 b^2 )))≥(8/3) let ab=x⇔(((1+2x)(2−x))/(x(2+x^2 )))≥(8/3) ⇔8x^3 +6x^2 +7x−6≤0 ab≤(1/2)(a^2 +b^2 )=(1/2)⇒ 8x^3 ≤1,7x≤(7/2),6x^2 ≤(3/2) ⇒8x^3 +6x^2 +7x−6≤1+(7/2)+(3/2)−6=0 ⇔((1/a)+(1/b))((a/(b^2 +1))+(b/(a^2 +1)))≥(8/3)

$$\left(\frac{{a}+{b}}{{ab}}\right)\left(\frac{{b}^{\mathrm{3}} +{b}+{a}^{\mathrm{3}} +{a}}{\mathrm{2}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right) \\ $$ $$\left({b}^{\mathrm{3}} +{a}^{\mathrm{3}} +{a}+{b}\right)=\left({a}+{b}\right)\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ab}+\mathrm{1}\right) \\ $$ $$=\left({a}+{b}\right)\left(\mathrm{2}−{ab}\right) \\ $$ $$\Leftrightarrow\frac{\left({a}+{b}\right)^{\mathrm{2}} \left(\mathrm{2}−{ab}\right)}{{ab}\left(\mathrm{2}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)} \\ $$ $$\left({a}+{b}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{ab} \\ $$ $$\Leftrightarrow\frac{\left(\mathrm{1}+\mathrm{2}{ab}\right)\left(\mathrm{2}−{ab}\right)}{{ab}\left(\mathrm{2}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)}\geqslant\frac{\mathrm{8}}{\mathrm{3}} \\ $$ $${let}\:{ab}={x}\Leftrightarrow\frac{\left(\mathrm{1}+\mathrm{2}{x}\right)\left(\mathrm{2}−{x}\right)}{{x}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)}\geqslant\frac{\mathrm{8}}{\mathrm{3}} \\ $$ $$\Leftrightarrow\mathrm{8}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{6}\leqslant\mathrm{0} \\ $$ $${ab}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow \\ $$ $$\mathrm{8}{x}^{\mathrm{3}} \leqslant\mathrm{1},\mathrm{7}{x}\leqslant\frac{\mathrm{7}}{\mathrm{2}},\mathrm{6}{x}^{\mathrm{2}} \leqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$ $$\Rightarrow\mathrm{8}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{6}\leqslant\mathrm{1}+\frac{\mathrm{7}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{6}=\mathrm{0} \\ $$ $$\Leftrightarrow\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right)\left(\frac{{a}}{{b}^{\mathrm{2}} +\mathrm{1}}+\frac{{b}}{{a}^{\mathrm{2}} +\mathrm{1}}\right)\geqslant\frac{\mathrm{8}}{\mathrm{3}} \\ $$ $$ \\ $$ $$ \\ $$

Commented by M±th+et+s last updated on 13/Jun/20

������ great work

Commented bymaths mind last updated on 13/Jun/20

thanx , i got answer for your post i will post it latter

$${thanx}\:\:,\:{i}\:{got}\:{answer}\:{for}\:{your}\:{post} \\ $$ $${i}\:{will}\:{post}\:{it}\:{latter} \\ $$

Commented by M±th+et+s last updated on 13/Jun/20

thank you so much . god bless you sir

$${thank}\:{you}\:{so}\:{much}\:. \\ $$ $${god}\:{bless}\:{you}\:{sir} \\ $$

Answered by 1549442205 last updated on 13/Jun/20

Putting a=cosϕ,b=sinϕ,ϕ∈[0;(π/2)].Then the given inequality becomes ((1/(cosϕ))+(1/(sinϕ)))(((sinϕ)/(cos^2 ϕ+1))+((cosϕ)/(sin^2 ϕ+1)))≥(8/3) ⇔(((cosϕ+sinϕ)(cos^3 ϕ+sin^3 ϕ+cosϕ+sinϕ))/(cosϕ.sinϕ(2+cos^2 ϕsin^2 ϕ)))≥(8/3) ⇔(((cosϕ+sinϕ)^2 (2−sinϕcosϕ))/(((sin2ϕ)/2).(2+((sin^2 ϕ)/4))))≥(8/3) ⇔(((1+sin2ϕ)(2−((sin2ϕ)/2)))/(sin2ϕ+((sin^3 ϕ)/8)))≥(8/3) ⇔3{2+(3/2)sin2ϕ−((sin^2 2ϕ)/2)}≥8sin2ϕ+sin^3 2ϕ ⇔sin^3 2ϕ+(3/2)sin^2 2ϕ+(7/2)sin2ϕ−6≤0 ⇔2sin^3 2ϕ+3sin^2 2ϕ+7sin2ϕ−12≤0 ⇔(sin2ϕ−1)(2sin^2 2ϕ+5sin2ϕ+12)≤0 The final inequality is always true because (2sin^2 2ϕ+5sin2ϕ+12)=2(sin2ϕ+(5/4))^2 +((71)/8)>0 and sin2ϕ≤1.Therefore the given inequality proved.The equality occurs if and only if sin2ϕ=1⇔a=b=((√2)/2)

$$\mathrm{Putting}\:\mathrm{a}=\mathrm{cos}\varphi,\mathrm{b}=\mathrm{sin}\varphi,\varphi\in\left[\mathrm{0};\frac{\pi}{\mathrm{2}}\right].\mathrm{Then} \\ $$ $$\mathrm{the}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{becomes}\: \\ $$ $$\left(\frac{\mathrm{1}}{\mathrm{cos}\varphi}+\frac{\mathrm{1}}{\mathrm{sin}\varphi}\right)\left(\frac{\mathrm{sin}\varphi}{\mathrm{cos}^{\mathrm{2}} \varphi+\mathrm{1}}+\frac{\mathrm{cos}\varphi}{\mathrm{sin}^{\mathrm{2}} \varphi+\mathrm{1}}\right)\geqslant\frac{\mathrm{8}}{\mathrm{3}} \\ $$ $$\Leftrightarrow\frac{\left(\mathrm{cos}\varphi+\mathrm{sin}\varphi\right)\left(\mathrm{cos}^{\mathrm{3}} \varphi+\mathrm{sin}^{\mathrm{3}} \varphi+\mathrm{cos}\varphi+\mathrm{sin}\varphi\right)}{\mathrm{cos}\varphi.\mathrm{sin}\varphi\left(\mathrm{2}+\mathrm{cos}^{\mathrm{2}} \varphi\mathrm{sin}^{\mathrm{2}} \varphi\right)}\geqslant\frac{\mathrm{8}}{\mathrm{3}} \\ $$ $$\Leftrightarrow\frac{\left(\mathrm{cos}\varphi+\mathrm{sin}\varphi\right)^{\mathrm{2}} \left(\mathrm{2}−\mathrm{sin}\varphi\mathrm{cos}\varphi\right)}{\frac{\mathrm{sin2}\varphi}{\mathrm{2}}.\left(\mathrm{2}+\frac{\mathrm{sin}^{\mathrm{2}} \varphi}{\mathrm{4}}\right)}\geqslant\frac{\mathrm{8}}{\mathrm{3}} \\ $$ $$\Leftrightarrow\frac{\left(\mathrm{1}+\mathrm{sin2}\varphi\right)\left(\mathrm{2}−\frac{\mathrm{sin2}\varphi}{\mathrm{2}}\right)}{\mathrm{sin2}\varphi+\frac{\mathrm{sin}^{\mathrm{3}} \varphi}{\mathrm{8}}}\geqslant\frac{\mathrm{8}}{\mathrm{3}} \\ $$ $$\Leftrightarrow\mathrm{3}\left\{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin2}\varphi−\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{2}\varphi}{\mathrm{2}}\right\}\geqslant\mathrm{8sin2}\varphi+\mathrm{sin}^{\mathrm{3}} \mathrm{2}\varphi \\ $$ $$\Leftrightarrow\mathrm{sin}^{\mathrm{3}} \mathrm{2}\varphi+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \mathrm{2}\varphi+\frac{\mathrm{7}}{\mathrm{2}}\mathrm{sin2}\varphi−\mathrm{6}\leqslant\mathrm{0} \\ $$ $$\Leftrightarrow\mathrm{2sin}^{\mathrm{3}} \mathrm{2}\varphi+\mathrm{3sin}^{\mathrm{2}} \mathrm{2}\varphi+\mathrm{7sin2}\varphi−\mathrm{12}\leqslant\mathrm{0} \\ $$ $$\Leftrightarrow\left(\mathrm{sin2}\varphi−\mathrm{1}\right)\left(\mathrm{2sin}^{\mathrm{2}} \mathrm{2}\varphi+\mathrm{5sin2}\varphi+\mathrm{12}\right)\leqslant\mathrm{0} \\ $$ $$\mathrm{The}\:\mathrm{final}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{always}\:\mathrm{true}\:\mathrm{because} \\ $$ $$\left(\mathrm{2sin}^{\mathrm{2}} \mathrm{2}\varphi+\mathrm{5sin2}\varphi+\mathrm{12}\right)=\mathrm{2}\left(\mathrm{sin2}\varphi+\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} +\frac{\mathrm{71}}{\mathrm{8}}>\mathrm{0} \\ $$ $$\mathrm{and}\:\mathrm{sin2}\varphi\leqslant\mathrm{1}.\mathrm{Therefore}\:\mathrm{the}\:\mathrm{given}\: \\ $$ $$\mathrm{inequality}\:\mathrm{proved}.\mathrm{The}\:\mathrm{equality}\:\mathrm{occurs} \\ $$ $$\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{sin2}\varphi=\mathrm{1}\Leftrightarrow\mathrm{a}=\mathrm{b}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$ $$ \\ $$ $$ \\ $$

Commented by M±th+et+s last updated on 13/Jun/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com