Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 98268 by mr W last updated on 16/Jun/20

let p(x) be a polynomial function of (n−1)^(th) degree and p(k)=k for k=1,2,3,...,n find p(0) and p(n+1). example: n=10

$${let}\:{p}\left({x}\right)\:{be}\:{a}\:{polynomial}\:{function}\:{of} \\ $$$$\left({n}−\mathrm{1}\right)^{{th}} \:{degree}\:{and} \\ $$$${p}\left({k}\right)={k}\:{for}\:{k}=\mathrm{1},\mathrm{2},\mathrm{3},...,{n} \\ $$$${find}\:{p}\left(\mathrm{0}\right)\:{and}\:{p}\left({n}+\mathrm{1}\right). \\ $$$${example}:\:{n}=\mathrm{10} \\ $$

Commented by MJS last updated on 13/Jun/20

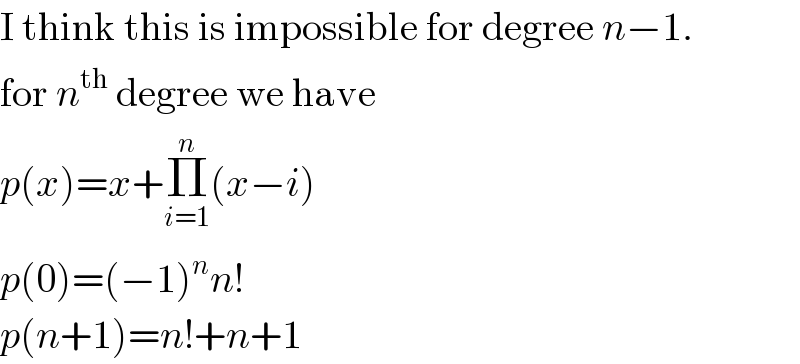
I think this is impossible for degree n−1. for n^(th) degree we have p(x)=x+Π_(i=1) ^n (x−i) p(0)=(−1)^n n! p(n+1)=n!+n+1

$$\mathrm{I}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{impossible}\:\mathrm{for}\:\mathrm{degree}\:{n}−\mathrm{1}. \\ $$$$\mathrm{for}\:{n}^{\mathrm{th}} \:\mathrm{degree}\:\mathrm{we}\:\mathrm{have} \\ $$$${p}\left({x}\right)={x}+\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\left({x}−{i}\right) \\ $$$${p}\left(\mathrm{0}\right)=\left(−\mathrm{1}\right)^{{n}} {n}! \\ $$$${p}\left({n}+\mathrm{1}\right)={n}!+{n}+\mathrm{1} \\ $$

Commented by mr W last updated on 13/Jun/20

thanks sir! for (n−1)^(th) degree we have n eqn. for n coefficients, so the function should be unique. can you explain why this is not possible? for n^(th) degree, the function p(x)=x+Π_(i=1) ^n (x−i) fulfills all conditions, but it is not unique, i think.

$${thanks}\:{sir}! \\ $$$${for}\:\left({n}−\mathrm{1}\right)^{{th}} \:{degree}\:{we}\:{have}\:{n}\:{eqn}. \\ $$$${for}\:{n}\:{coefficients},\:{so}\:{the}\:{function} \\ $$$${should}\:{be}\:{unique}.\:{can}\:{you}\:{explain} \\ $$$${why}\:{this}\:{is}\:{not}\:{possible}? \\ $$$${for}\:{n}^{{th}} \:{degree},\:{the}\:{function}\: \\ $$$${p}\left({x}\right)={x}+\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\left({x}−{i}\right) \\ $$$${fulfills}\:{all}\:{conditions},\:{but}\:{it}\:{is}\:{not} \\ $$$${unique},\:{i}\:{think}. \\ $$

Commented by MJS last updated on 13/Jun/20

n=3 ax^2 +bx+c=y x=y=1: a+b+c=1 x=y=2: 4a+2b+c=2 x=y=3: 9a+3b+c=3 solving leads to a=c=0∧b=1 p(x)=x for n=4 ax^3 +bx^2 +cx+d=y ... a=b=d=0∧c=1 ⇒ p(x)=x ...

$${n}=\mathrm{3} \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}={y} \\ $$$${x}={y}=\mathrm{1}:\:{a}+{b}+{c}=\mathrm{1} \\ $$$${x}={y}=\mathrm{2}:\:\mathrm{4}{a}+\mathrm{2}{b}+{c}=\mathrm{2} \\ $$$${x}={y}=\mathrm{3}:\:\mathrm{9}{a}+\mathrm{3}{b}+{c}=\mathrm{3} \\ $$$$\mathrm{solving}\:\mathrm{leads}\:\mathrm{to}\:{a}={c}=\mathrm{0}\wedge{b}=\mathrm{1} \\ $$$${p}\left({x}\right)={x} \\ $$$$\mathrm{for}\:{n}=\mathrm{4} \\ $$$${ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}={y} \\ $$$$... \\ $$$${a}={b}={d}=\mathrm{0}\wedge{c}=\mathrm{1}\:\Rightarrow\:{p}\left({x}\right)={x} \\ $$$$... \\ $$

Commented by mr W last updated on 13/Jun/20

now clear sir, thanks! all points (k,k) with k=1..n lie on the line y=x, so p(x)=x is indeed always a suitable polynomial for the solution. what do you think? if p(k)=(−1)^(k+1) k, does the (n−1)^(th) degree polynomial function exist?

$${now}\:{clear}\:{sir},\:{thanks}! \\ $$$${all}\:{points}\:\left({k},{k}\right)\:{with}\:{k}=\mathrm{1}..{n}\:{lie}\:{on} \\ $$$${the}\:{line}\:{y}={x},\:{so}\:{p}\left({x}\right)={x}\:{is}\:{indeed} \\ $$$${always}\:{a}\:{suitable}\:{polynomial}\:{for} \\ $$$${the}\:{solution}. \\ $$$${what}\:{do}\:{you}\:{think}?\:{if}\:{p}\left({k}\right)=\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} {k}, \\ $$$${does}\:{the}\:\left({n}−\mathrm{1}\right)^{{th}} \:{degree}\:{polynomial} \\ $$$${function}\:{exist}? \\ $$

Commented by MJS last updated on 14/Jun/20

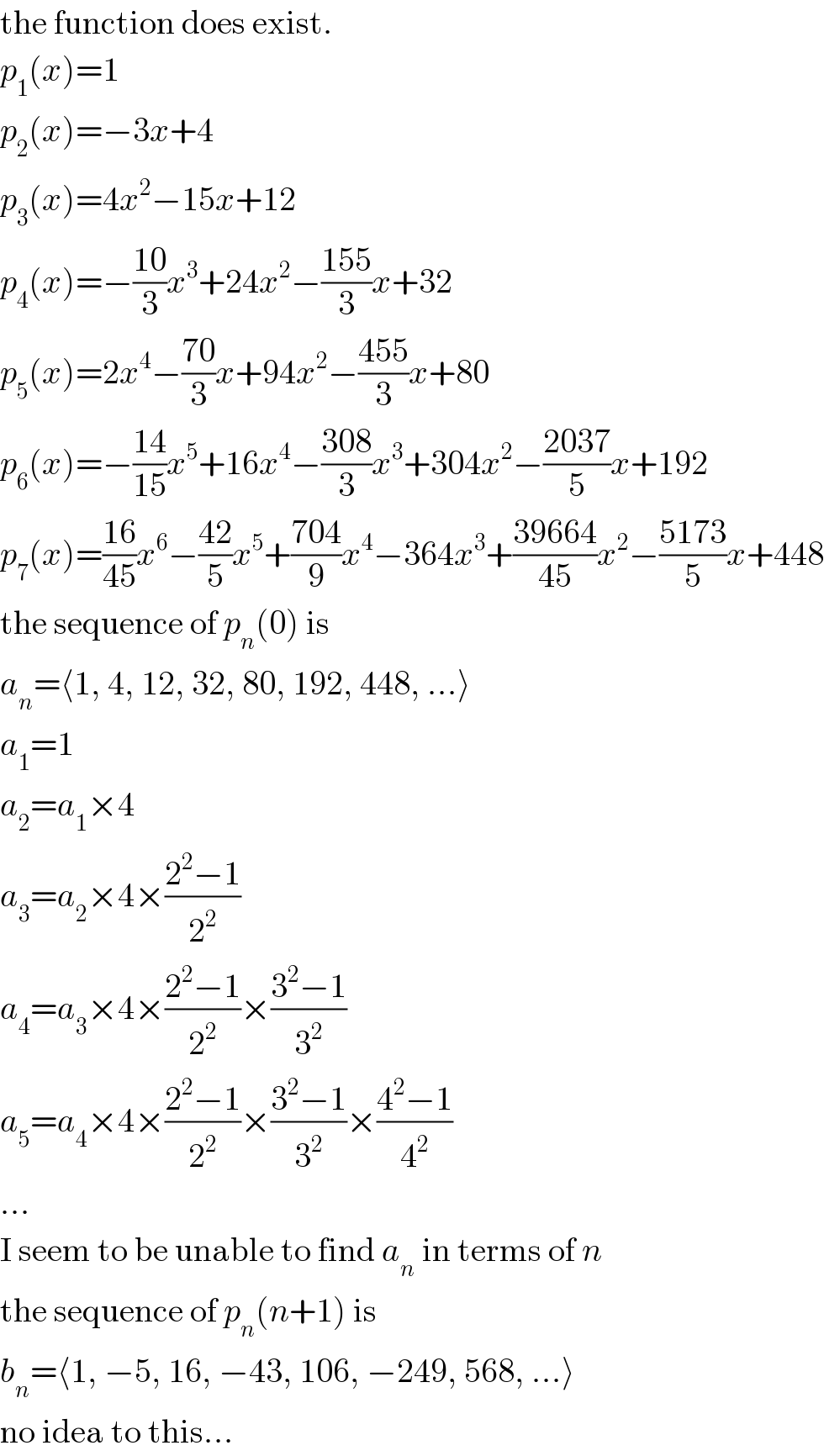
the function does exist. p_1 (x)=1 p_2 (x)=−3x+4 p_3 (x)=4x^2 −15x+12 p_4 (x)=−((10)/3)x^3 +24x^2 −((155)/3)x+32 p_5 (x)=2x^4 −((70)/3)x+94x^2 −((455)/3)x+80 p_6 (x)=−((14)/(15))x^5 +16x^4 −((308)/3)x^3 +304x^2 −((2037)/5)x+192 p_7 (x)=((16)/(45))x^6 −((42)/5)x^5 +((704)/9)x^4 −364x^3 +((39664)/(45))x^2 −((5173)/5)x+448 the sequence of p_n (0) is a_n =⟨1, 4, 12, 32, 80, 192, 448, ...⟩ a_1 =1 a_2 =a_1 ×4 a_3 =a_2 ×4×((2^2 −1)/2^2 ) a_4 =a_3 ×4×((2^2 −1)/2^2 )×((3^2 −1)/3^2 ) a_5 =a_4 ×4×((2^2 −1)/2^2 )×((3^2 −1)/3^2 )×((4^2 −1)/4^2 ) ... I seem to be unable to find a_n in terms of n the sequence of p_n (n+1) is b_n =⟨1, −5, 16, −43, 106, −249, 568, ...⟩ no idea to this...

$$\mathrm{the}\:\mathrm{function}\:\mathrm{does}\:\mathrm{exist}. \\ $$$${p}_{\mathrm{1}} \left({x}\right)=\mathrm{1} \\ $$$${p}_{\mathrm{2}} \left({x}\right)=−\mathrm{3}{x}+\mathrm{4} \\ $$$${p}_{\mathrm{3}} \left({x}\right)=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{15}{x}+\mathrm{12} \\ $$$${p}_{\mathrm{4}} \left({x}\right)=−\frac{\mathrm{10}}{\mathrm{3}}{x}^{\mathrm{3}} +\mathrm{24}{x}^{\mathrm{2}} −\frac{\mathrm{155}}{\mathrm{3}}{x}+\mathrm{32} \\ $$$${p}_{\mathrm{5}} \left({x}\right)=\mathrm{2}{x}^{\mathrm{4}} −\frac{\mathrm{70}}{\mathrm{3}}{x}+\mathrm{94}{x}^{\mathrm{2}} −\frac{\mathrm{455}}{\mathrm{3}}{x}+\mathrm{80} \\ $$$${p}_{\mathrm{6}} \left({x}\right)=−\frac{\mathrm{14}}{\mathrm{15}}{x}^{\mathrm{5}} +\mathrm{16}{x}^{\mathrm{4}} −\frac{\mathrm{308}}{\mathrm{3}}{x}^{\mathrm{3}} +\mathrm{304}{x}^{\mathrm{2}} −\frac{\mathrm{2037}}{\mathrm{5}}{x}+\mathrm{192} \\ $$$${p}_{\mathrm{7}} \left({x}\right)=\frac{\mathrm{16}}{\mathrm{45}}{x}^{\mathrm{6}} −\frac{\mathrm{42}}{\mathrm{5}}{x}^{\mathrm{5}} +\frac{\mathrm{704}}{\mathrm{9}}{x}^{\mathrm{4}} −\mathrm{364}{x}^{\mathrm{3}} +\frac{\mathrm{39664}}{\mathrm{45}}{x}^{\mathrm{2}} −\frac{\mathrm{5173}}{\mathrm{5}}{x}+\mathrm{448} \\ $$$$\mathrm{the}\:\mathrm{sequence}\:\mathrm{of}\:{p}_{{n}} \left(\mathrm{0}\right)\:\mathrm{is} \\ $$$${a}_{{n}} =\langle\mathrm{1},\:\mathrm{4},\:\mathrm{12},\:\mathrm{32},\:\mathrm{80},\:\mathrm{192},\:\mathrm{448},\:...\rangle \\ $$$${a}_{\mathrm{1}} =\mathrm{1} \\ $$$${a}_{\mathrm{2}} ={a}_{\mathrm{1}} ×\mathrm{4} \\ $$$${a}_{\mathrm{3}} ={a}_{\mathrm{2}} ×\mathrm{4}×\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2}} } \\ $$$${a}_{\mathrm{4}} ={a}_{\mathrm{3}} ×\mathrm{4}×\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }×\frac{\mathrm{3}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}^{\mathrm{2}} } \\ $$$${a}_{\mathrm{5}} ={a}_{\mathrm{4}} ×\mathrm{4}×\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }×\frac{\mathrm{3}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }×\frac{\mathrm{4}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}^{\mathrm{2}} } \\ $$$$... \\ $$$$\mathrm{I}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{be}\:\mathrm{unable}\:\mathrm{to}\:\mathrm{find}\:{a}_{{n}} \:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:{n} \\ $$$$\mathrm{the}\:\mathrm{sequence}\:\mathrm{of}\:{p}_{{n}} \left({n}+\mathrm{1}\right)\:\mathrm{is} \\ $$$${b}_{{n}} =\langle\mathrm{1},\:−\mathrm{5},\:\mathrm{16},\:−\mathrm{43},\:\mathrm{106},\:−\mathrm{249},\:\mathrm{568},\:...\rangle \\ $$$$\mathrm{no}\:\mathrm{idea}\:\mathrm{to}\:\mathrm{this}... \\ $$

Commented by mr W last updated on 14/Jun/20

thanks very much sir! is following the right path to solve? say p_n (x)=Σ_(k=0) ^(n−1) c_(n,k) x^k p_n (r)=Σ_(k=0) ^(n−1) c_(n,k) r^k =(−1)^(r+1) r [(1,1,1,(...),1),(1,2,2^2 ,(...),2^(n−1) ),(1,3,3^2 ,(...),3^(n−1) ),((...),(...),(...),(...),(...)),(1,n,n^2 ,(...),n^(n−1) ) ] ((c_(n,0) ),(c_(n,1) ),(c_(n,2) ),((...)),(c_(n,n−1) ) )= ((1),((−2)),(3),((...)),(((−1)^(n+1) n)) ) ⇒ ((c_(n,0) ),(c_(n,1) ),(c_(n,2) ),((...)),(c_(n,n−1) ) )= [(1,1,1,(...),1),(1,2,2^2 ,(...),2^(n−1) ),(1,3,3^2 ,(...),3^(n−1) ),((...),(...),(...),(...),(...)),(1,n,n^2 ,(...),n^(n−1) ) ]^(−1) ((1),((−2)),(3),((...)),(((−1)^(n+1) n)) )

$${thanks}\:{very}\:{much}\:{sir}! \\ $$$${is}\:{following}\:{the}\:{right}\:{path}\:{to}\:{solve}? \\ $$$${say}\:{p}_{{n}} \left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{c}_{{n},{k}} {x}^{{k}} \\ $$$${p}_{{n}} \left({r}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{c}_{{n},{k}} {r}^{{k}} =\left(−\mathrm{1}\right)^{{r}+\mathrm{1}} {r} \\ $$$$\begin{bmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{...}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{2}^{\mathrm{2}} }&{...}&{\mathrm{2}^{{n}−\mathrm{1}} }\\{\mathrm{1}}&{\mathrm{3}}&{\mathrm{3}^{\mathrm{2}} }&{...}&{\mathrm{3}^{{n}−\mathrm{1}} }\\{...}&{...}&{...}&{...}&{...}\\{\mathrm{1}}&{{n}}&{{n}^{\mathrm{2}} }&{...}&{{n}^{{n}−\mathrm{1}} }\end{bmatrix}\begin{pmatrix}{{c}_{{n},\mathrm{0}} }\\{{c}_{{n},\mathrm{1}} }\\{{c}_{{n},\mathrm{2}} }\\{...}\\{{c}_{{n},{n}−\mathrm{1}} }\end{pmatrix}=\begin{pmatrix}{\mathrm{1}}\\{−\mathrm{2}}\\{\mathrm{3}}\\{...}\\{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}}\end{pmatrix} \\ $$$$\Rightarrow\begin{pmatrix}{{c}_{{n},\mathrm{0}} }\\{{c}_{{n},\mathrm{1}} }\\{{c}_{{n},\mathrm{2}} }\\{...}\\{{c}_{{n},{n}−\mathrm{1}} }\end{pmatrix}=\begin{bmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{...}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{2}^{\mathrm{2}} }&{...}&{\mathrm{2}^{{n}−\mathrm{1}} }\\{\mathrm{1}}&{\mathrm{3}}&{\mathrm{3}^{\mathrm{2}} }&{...}&{\mathrm{3}^{{n}−\mathrm{1}} }\\{...}&{...}&{...}&{...}&{...}\\{\mathrm{1}}&{{n}}&{{n}^{\mathrm{2}} }&{...}&{{n}^{{n}−\mathrm{1}} }\end{bmatrix}^{−\mathrm{1}} \begin{pmatrix}{\mathrm{1}}\\{−\mathrm{2}}\\{\mathrm{3}}\\{...}\\{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}}\end{pmatrix} \\ $$

Commented by MJS last updated on 15/Jun/20

yes

$${yes} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com