Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 98271 by Ar Brandon last updated on 12/Jun/20

$$\mathcal{G}{\mathrm{ivenU}}_{\mathrm{n}}={\int }_0^1{\mathrm{x}}^{\mathrm{n}}\sqrt{1-\mathrm{x}}\mathrm{dx}\mathrm{n}\in \mathbb{N},\mathrm{show}\mathrm{that}$$$${\mathrm{U}}_{\mathrm{n}}=\frac{2^{\mathrm{n}+2}\mathrm{n}!(\mathrm{n}+1)}{(2\mathrm{n}+3)!}$$

Commented by Ar Brandon last updated on 12/Jun/20

Thanks �� But, it really isn't clear to me. Any explanations please ?��

Commented by PRITHWISH SEN 2 last updated on 12/Jun/20

$$\mathrm{then}{\mathrm{U}}_{\mathrm{n}}=\frac{2\mathrm{n}}{2\mathrm{n}+3}.\frac{2(\mathrm{n}-1)}{2\mathrm{n}+1}......\frac{4}{7}.\frac{2}{5}.\frac{2}{3}$$$$=\frac{2^{\mathrm{n}}\{\mathrm{n}(\mathrm{n}-1)(\mathrm{n}-2)(\mathrm{n}-3)......2.1\}.2}{(2\mathrm{n}+3)(2\mathrm{n}+1).........7.5.3}$$$$=\frac{2^{\mathrm{n}+1}.\mathrm{n}!}{(2\mathrm{n}+3)!}\times 2^{\mathrm{n}+1}\{(\mathrm{n}+1)\mathrm{n}(\mathrm{n}-1)........2.1\}$$$$=\frac{2^{2\mathbf{n}+2}\mathbf{n}!(\mathbf{n}+1)!}{(2\mathbf{n}+3)!}\mathbf{I}\mathbf{got}\mathbf{this}\mathbf{please}\mathbf{check}$$

Commented by Ar Brandon last updated on 12/Jun/20

$${\mathrm{I}}^{\prime }\mathrm{m}\mathrm{stucked}\mathrm{here}.\mathrm{Can}\mathrm{anyone}\mathrm{help}\mathrm{me}\mathrm{out},\mathrm{please}?$$

Commented by Ar Brandon last updated on 12/Jun/20

Commented by PRITHWISH SEN 2 last updated on 20/Jul/20

$$\mathrm{I}\mathrm{did}\mathrm{not}\mathrm{do}\mathrm{anything}\mathrm{I}\mathrm{just}\mathrm{expanded}\mathrm{your}\mathrm{expression}$$$${\mathrm{U}}_{\mathrm{n}}=\frac{2\mathrm{n}}{2\mathrm{n}+3}{\mathrm{U}}_{\mathrm{n}-1}\mathrm{then}{\mathrm{U}}_{\mathrm{n}-1}=\frac{2(\mathrm{n}-1)}{2(\mathrm{n}-1)+3}{\mathrm{U}}_{\mathrm{n}-2}$$$$\Rightarrow {\mathrm{U}}_{\mathrm{n}-1}=\frac{2(\mathrm{n}-1)}{2\mathrm{n}+1}{\mathrm{U}}_{\mathrm{n}-2}\mathrm{and}\mathrm{likewise}\mathrm{you}\mathrm{can}\mathrm{get}$$$$\mathrm{by}\mathrm{putting}\mathrm{n}=\mathrm{n}-2,\mathrm{n}-3\mathrm{and}\mathrm{so}\mathrm{on}$$$$\mathrm{now}\mathrm{for}{\mathrm{U}}_1=\frac{2}{5}{\mathrm{U}}_0{\mathrm{andU}}_0={\int }_0^1{\mathrm{x}}^0\sqrt{1-\mathrm{x}}\mathrm{dx}=\frac{2}{3}$$$$\mathrm{I}\mathrm{think}\mathrm{now}\mathrm{it}\mathrm{makes}\mathrm{sense}$$

Answered by smridha last updated on 12/Jun/20

$$\mathit{l}\mathit{e}\mathit{t}\mathit{x}=\sin {}^2\mathit{\theta }\mathit{s}\mathit{o}$$$$2{\int }_0^{\frac{\mathit{\pi }}{2}}{\mathit{s}\mathit{i}\mathit{n}}^{(2\mathit{n}+1)}\mathit{\theta }{\mathit{c}\mathit{o}\mathit{s}}^2\mathit{\theta }\mathit{d}\mathit{\theta }$$$$=\frac{\mathbf{\Gamma }(\mathit{n}+1).\mathbf{\Gamma }\left(\frac{3}{2}\right)}{\mathbf{\Gamma }(\mathit{n}+\frac{5}{2})}=\frac{\mathit{n}!\sqrt{\mathit{\pi }}}{(2\mathit{n}+3).\mathbf{\Gamma }(\mathit{n}+\frac{3}{2})}$$$$\mathit{I}\mathit{t}\mathit{h}\mathit{i}\mathit{n}\mathit{k}\mathit{n}\mathit{o}\mathit{w}\mathit{y}\mathit{o}\mathit{u}\mathit{c}\mathit{a}\mathit{n}\mathit{e}\mathit{a}\mathit{s}\mathit{y}\mathit{l}\mathit{y}$$$$\mathit{g}\mathit{e}\mathit{t}\mathit{y}\mathit{o}\mathit{u}\mathit{r}\mathit{a}\mathit{n}\mathit{s}.$$

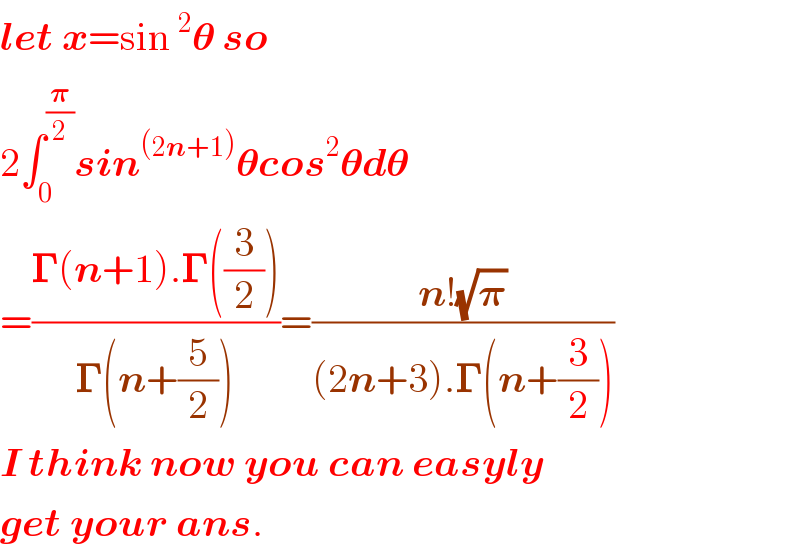
Commented by PRITHWISH SEN 2 last updated on 13/Jun/20

$$\mathrm{wow}!\mathrm{excellent}\mathrm{sir}.$$

Commented by smridha last updated on 13/Jun/20

$$\mathit{t}\mathit{h}\mathit{a}\mathit{n}\mathit{k}\mathit{s}..$$

Commented by PRITHWISH SEN 2 last updated on 13/Jun/20

$$\mathrm{welcome}$$

Commented by Ar Brandon last updated on 13/Jun/20

Hum, thank you ��

Answered by Dwaipayan Shikari last updated on 01/Nov/20

$${\int }_0^1{x}^n{(1-x)}^{\frac{1}{2}}dx$$$$={\int }_0^1{x}^{n+1-1}{x}^{\frac{3}{2}-1}dx$$$$=\beta (n+1,\frac{3}{2})=\frac{\mathrm{\Gamma }(n+1)\mathrm{\Gamma }\left(\frac{3}{2}\right)}{\mathrm{\Gamma }(n+\frac{5}{2})}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com