
Question and Answers Forum
Question Number 98305 by mathmax by abdo last updated on 12/Jun/20
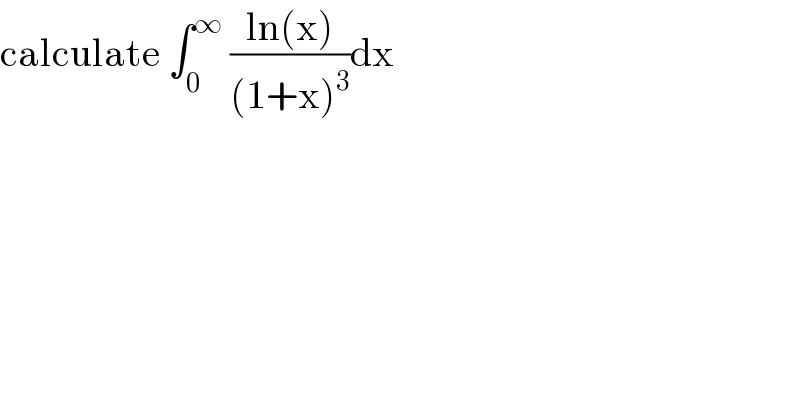
Answered by maths mind last updated on 13/Jun/20
![=∫_0 ^1 ((ln(t))/((1+t)^3 ))dt−∫_0 ^1 ((tln(t))/((1+t)^3 )) =2∫((ln(t))/((1+t)^3 ))dt−∫_0 ^1 ((ln(t))/((1+t)^2 ))=−(−2∫_0 ^1 ((ln(t)dt)/((1+t)^3 ))+∫_0 ^1 ((ln(t)dt)/((1+t)^2 )))=S ∫_y ^1 ((ln(t))/((a+t)^2 ))dt=[−((ln(t))/(a+t))]_y ^1 +∫_y ^1 (dt/(t(a+t))) =((ln(y))/(a+y))−(1/a){ln(y)+ln(1+a)−ln(a)} =((aln(y)−aln(y)−yln(y))/(a(a+y)))−((ln(1+a))/a)+((ln(a))/a) lim_(y→0) ∫_y ^1 ((ln(t))/((t+a)^2 ))dt=(1/a)ln((a/(a+1)))=f(a) f′(a)=−((ln((a/(a+1))))/a^2 )+(1/a)((1/a)−(1/(1+a))) S=−(f(1)+f′(1)) =−(ln((1/2))−ln((1/2))+(1/2))=−(1/2)](Q98321.png)
Commented by abdomathmax last updated on 13/Jun/20

Answered by abdomathmax last updated on 14/Jun/20
![A =∫_0 ^∞ ((ln(x))/((1+x)^3 ))dx ⇒A=∫_0 ^1 ((ln(x))/((1+x)^3 ))dx +∫_1 ^(+∞) ((lnx)/((1+x)^3 ))dx(→x=(1/t)) =∫_0 ^1 ((lnx)/((1+x)^3 ))dx −∫_0 ^1 ((−lnt)/((1+(1/t))^3 ))(−(dt/t^2 )) =∫_0 ^1 ((lnx)/((1+x)^3 ))dx−∫_0 ^1 ((tlnt)/((1+t)^3 ))dt =∫_0 ^1 (((1−x)lnx)/((1+x)^3 )) dx =−∫_0 ^1 (((x+1−2)lnx)/((1+x)^3 )))dx =−∫_0 ^1 ((lnx)/((1+x)^2 ))dx +2 ∫_0 ^1 ((lnx)/((1+x)^3 ))dx =ln(2)+2 ∫_0 ^1 ((lnx)/((1+x)^3 ))dx by parts u^′ =(1+x)^(−3) ∫_0 ^1 ((ln(x))/((1+x)^3 ))dx =[((1/2)−(1/(2(1+x)^2 )))ln(x)]_0 ^1 −∫_0 ^1 ((1/2)−(1/(2(1+x)^2 )))(dx/x) =−(1/2) ∫_0 ^1 (((x^2 +2x)/(x(1+x)^2 )))dx =−(1/2) ∫_0 ^1 ((x+2)/((1+x)^2 ))dx =−(1/2) ∫_0 ^1 ((x+1+1)/((1+x)^2 ))dx =−(1/2) ∫_0 ^1 (dx/(1+x)) −(1/2) ∫_0 ^1 (dx/((1+x)^2 )) =−(1/2)ln(2)+(1/2)[(1/(x+1))]_0 ^1 =−((ln(2))/2) +(1/2)(−(1/2)) =−((ln(2))/2)−(1/4) ⇒ A =ln(2)+2(−((ln2)/2)−(1/4)) A=−(1/2)](Q98523.png)
| ||
Question and Answers Forum | ||
Question Number 98305 by mathmax by abdo last updated on 12/Jun/20 | ||
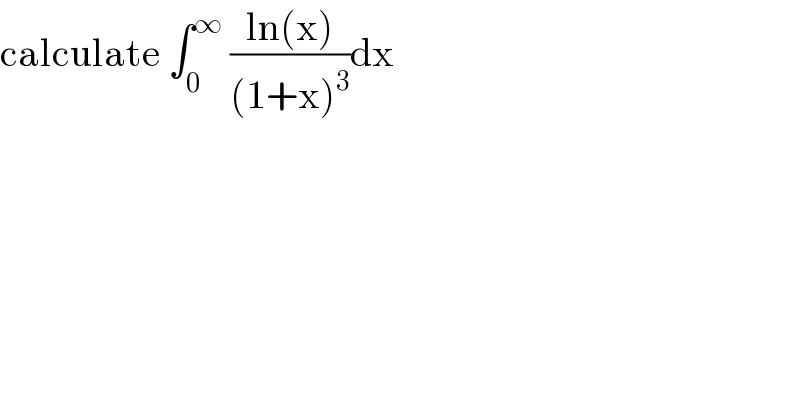 | ||
Answered by maths mind last updated on 13/Jun/20 | ||
![=∫_0 ^1 ((ln(t))/((1+t)^3 ))dt−∫_0 ^1 ((tln(t))/((1+t)^3 )) =2∫((ln(t))/((1+t)^3 ))dt−∫_0 ^1 ((ln(t))/((1+t)^2 ))=−(−2∫_0 ^1 ((ln(t)dt)/((1+t)^3 ))+∫_0 ^1 ((ln(t)dt)/((1+t)^2 )))=S ∫_y ^1 ((ln(t))/((a+t)^2 ))dt=[−((ln(t))/(a+t))]_y ^1 +∫_y ^1 (dt/(t(a+t))) =((ln(y))/(a+y))−(1/a){ln(y)+ln(1+a)−ln(a)} =((aln(y)−aln(y)−yln(y))/(a(a+y)))−((ln(1+a))/a)+((ln(a))/a) lim_(y→0) ∫_y ^1 ((ln(t))/((t+a)^2 ))dt=(1/a)ln((a/(a+1)))=f(a) f′(a)=−((ln((a/(a+1))))/a^2 )+(1/a)((1/a)−(1/(1+a))) S=−(f(1)+f′(1)) =−(ln((1/2))−ln((1/2))+(1/2))=−(1/2)](Q98321.png) | ||
| ||
Commented by abdomathmax last updated on 13/Jun/20 | ||
 | ||
Answered by abdomathmax last updated on 14/Jun/20 | ||
![A =∫_0 ^∞ ((ln(x))/((1+x)^3 ))dx ⇒A=∫_0 ^1 ((ln(x))/((1+x)^3 ))dx +∫_1 ^(+∞) ((lnx)/((1+x)^3 ))dx(→x=(1/t)) =∫_0 ^1 ((lnx)/((1+x)^3 ))dx −∫_0 ^1 ((−lnt)/((1+(1/t))^3 ))(−(dt/t^2 )) =∫_0 ^1 ((lnx)/((1+x)^3 ))dx−∫_0 ^1 ((tlnt)/((1+t)^3 ))dt =∫_0 ^1 (((1−x)lnx)/((1+x)^3 )) dx =−∫_0 ^1 (((x+1−2)lnx)/((1+x)^3 )))dx =−∫_0 ^1 ((lnx)/((1+x)^2 ))dx +2 ∫_0 ^1 ((lnx)/((1+x)^3 ))dx =ln(2)+2 ∫_0 ^1 ((lnx)/((1+x)^3 ))dx by parts u^′ =(1+x)^(−3) ∫_0 ^1 ((ln(x))/((1+x)^3 ))dx =[((1/2)−(1/(2(1+x)^2 )))ln(x)]_0 ^1 −∫_0 ^1 ((1/2)−(1/(2(1+x)^2 )))(dx/x) =−(1/2) ∫_0 ^1 (((x^2 +2x)/(x(1+x)^2 )))dx =−(1/2) ∫_0 ^1 ((x+2)/((1+x)^2 ))dx =−(1/2) ∫_0 ^1 ((x+1+1)/((1+x)^2 ))dx =−(1/2) ∫_0 ^1 (dx/(1+x)) −(1/2) ∫_0 ^1 (dx/((1+x)^2 )) =−(1/2)ln(2)+(1/2)[(1/(x+1))]_0 ^1 =−((ln(2))/2) +(1/2)(−(1/2)) =−((ln(2))/2)−(1/4) ⇒ A =ln(2)+2(−((ln2)/2)−(1/4)) A=−(1/2)](Q98523.png) | ||
| ||