Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 98342 by Lekhraj last updated on 13/Jun/20

Commented by MJS last updated on 13/Jun/20

$$29$$$$n=29+30k$$

Commented by Lekhraj last updated on 13/Jun/20

$$\mathrm{How}?\mathrm{Explain}$$

Answered by Rasheed.Sindhi last updated on 15/Jun/20

$$1+2^1+2^2+2^3+...+2^n\equiv 0\left(mod77\right)$$$$\Rightarrow 2^{n+1}-1\equiv 0\left(mod77\right)$$$$\Rightarrow 2^{n+1}\equiv 1\left(mod77\right)$$$$\mathrm{Observing}\mathrm{all}\mathrm{powers}\mathrm{of}2$$$$(2,2^2,...,2^{30})\mathrm{we}\mathrm{achieve}\mathrm{that}$$$$2^{30}\mathrm{is}\mathrm{smallest}\mathrm{power}\mathrm{such}\mathrm{that}$$$$2^{30}\equiv 1\left(mod77\right)$$$$\therefore n+1=30\Rightarrow n=29$$

Commented by MJS last updated on 17/Jun/20

$$2^{n+1}-1=77m$$$$2^{n+1}=77m+1\Rightarrow m=2k-1$$$$2^{n+1}=154k-76$$$$2^n=77k-38$$$$\mathrm{we}\mathrm{can}\mathrm{now}\mathrm{try}\mathrm{for}k$$$$\mathrm{anyway}\mathrm{I}\mathrm{think}\mathrm{we}\mathrm{can}\mathrm{only}\mathrm{try}...$$

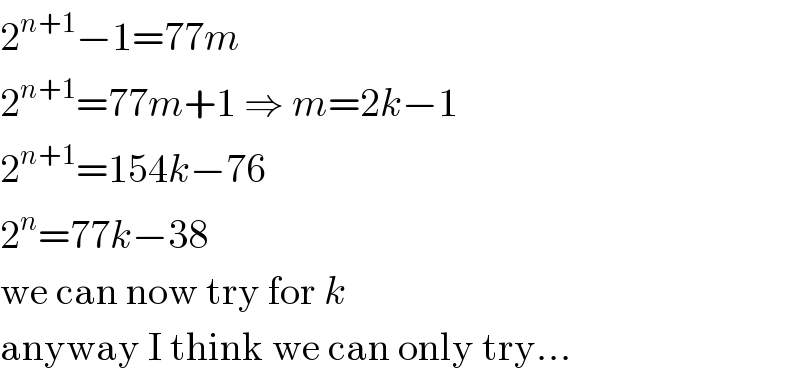
Commented by Rasheed.Sindhi last updated on 17/Jun/20

$$2^{n+1}=77m+1\Rightarrow m=2k-1$$$$$$

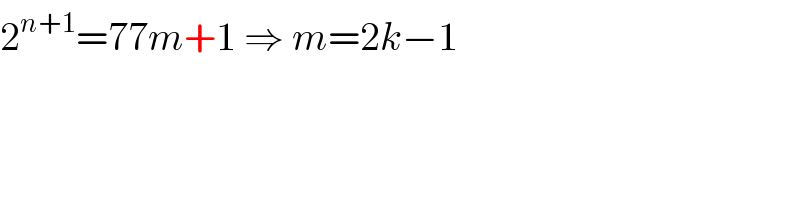
Commented by MJS last updated on 17/Jun/20

$$\mathrm{thank}\mathrm{you},\mathrm{I}\mathrm{corrected}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com