Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 98380 by Rio Michael last updated on 13/Jun/20

let {u_n } and {v_n } be sequences defined by u_0 = 9, u_(n+1) = (1/2)u_n −3. v_n = u_n + 6. Calculate P_n = Σ_(i=0) ^n V_i in terms of n, the deduce Q_n = Σ_(i=0) ^n u_i using the above expressions find lim_(x→∞) Q_n .

$$\mathrm{let}\:\left\{{u}_{{n}} \right\}\:\mathrm{and}\:\left\{{v}_{{n}} \right\}\:\mathrm{be}\:\mathrm{sequences}\:\mathrm{defined}\:\mathrm{by} \\ $$$$\:{u}_{\mathrm{0}} \:=\:\mathrm{9},\:{u}_{{n}+\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}{u}_{{n}} −\mathrm{3}. \\ $$$${v}_{{n}} \:=\:{u}_{{n}} \:+\:\mathrm{6}. \\ $$$$\mathrm{Calculate}\:{P}_{{n}} \:=\:\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{V}_{{i}} \:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:{n},\:\mathrm{the}\:\mathrm{deduce}\:{Q}_{{n}} \:=\:\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{u}_{{i}} \\ $$$$\mathrm{using}\:\mathrm{the}\:\mathrm{above}\:\mathrm{expressions}\:\mathrm{find} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{Q}_{{n}} \:. \\ $$

Answered by Aziztisffola last updated on 13/Jun/20

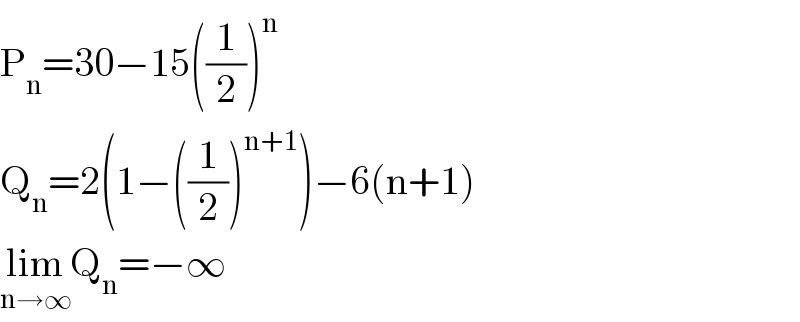
P_n =30−15((1/2))^n Q_n =2(1−((1/2))^(n+1) )−6(n+1) lim_(n→∞) Q_n =−∞

$$\mathrm{P}_{\mathrm{n}} =\mathrm{30}−\mathrm{15}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}} \\ $$$$\mathrm{Q}_{\mathrm{n}} =\mathrm{2}\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}+\mathrm{1}} \right)−\mathrm{6}\left(\mathrm{n}+\mathrm{1}\right) \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}Q}_{\mathrm{n}} =−\infty \\ $$

Answered by mr W last updated on 13/Jun/20

u_(n+1) =(1/2)u_n −3 u_(n+1) +6=(1/2)(u_n +6) ⇒u_n +6=(u_0 +6)((1/2))^n =((15)/2^n ) ⇒u_n =((15)/2^n )−6 ⇒v_n =((15)/2^n ) P_n =Σ_(i=0) ^n v_i =15×((1−(1/2^(n+1) ))/(1−(1/2)))=30(1−(1/2^(n+1) )) Q_n =Σ_(i=0) ^n u_i =Σ_(i=0) ^n (v_i −6)=30(1−(1/2^(n+1) ))−6(n+1) lim_(n→∞) Q_n =−∞

$${u}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}{u}_{{n}} −\mathrm{3} \\ $$$${u}_{{n}+\mathrm{1}} +\mathrm{6}=\frac{\mathrm{1}}{\mathrm{2}}\left({u}_{{n}} +\mathrm{6}\right) \\ $$$$\Rightarrow{u}_{{n}} +\mathrm{6}=\left({u}_{\mathrm{0}} +\mathrm{6}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} =\frac{\mathrm{15}}{\mathrm{2}^{{n}} } \\ $$$$\Rightarrow{u}_{{n}} =\frac{\mathrm{15}}{\mathrm{2}^{{n}} }−\mathrm{6} \\ $$$$\Rightarrow{v}_{{n}} =\frac{\mathrm{15}}{\mathrm{2}^{{n}} } \\ $$$${P}_{{n}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{v}_{{i}} =\mathrm{15}×\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{30}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\right) \\ $$$${Q}_{{n}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{u}_{{i}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\left({v}_{{i}} −\mathrm{6}\right)=\mathrm{30}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\right)−\mathrm{6}\left({n}+\mathrm{1}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{Q}_{{n}} =−\infty \\ $$

Commented by Rio Michael last updated on 13/Jun/20

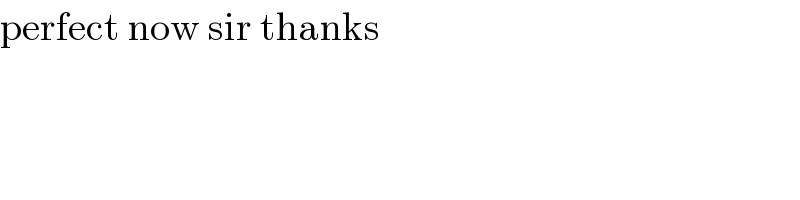
perfect now sir thanks

$$\mathrm{perfect}\:\mathrm{now}\:\mathrm{sir}\:\mathrm{thanks} \\ $$

Commented by Rio Michael last updated on 13/Jun/20

sir that is correct. thanks to you both. my worry is: why (n +1) ? i know ΣV_i = Σu_i + Σ6 ⇒ Σu_i = ΣV_i −Σ6 why will it not equal 30[1−((1/2))^n ]−6n instead it equals 30 [1−((1/2))^(n+1) ]−6n−6

$$\mathrm{sir}\:\mathrm{that}\:\mathrm{is}\:\mathrm{correct}.\:\mathrm{thanks}\:\mathrm{to}\:\mathrm{you}\:\mathrm{both}. \\ $$$$\mathrm{my}\:\mathrm{worry}\:\mathrm{is}:\:\mathrm{why}\:\left({n}\:+\mathrm{1}\right)\:? \\ $$$$\mathrm{i}\:\mathrm{know}\:\Sigma{V}_{{i}} \:=\:\Sigma{u}_{{i}} \:+\:\Sigma\mathrm{6}\:\Rightarrow\:\Sigma{u}_{{i}} \:=\:\Sigma{V}_{{i}} \:−\Sigma\mathrm{6}\: \\ $$$$\mathrm{why}\:\mathrm{will}\:\mathrm{it}\:\mathrm{not}\:\mathrm{equal}\:\mathrm{30}\left[\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \right]−\mathrm{6}{n}\:\:\mathrm{instead}\:\mathrm{it}\:\mathrm{equals} \\ $$$$\:\mathrm{30}\:\left[\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}+\mathrm{1}} \right]−\mathrm{6}{n}−\mathrm{6} \\ $$

Commented by mr W last updated on 13/Jun/20

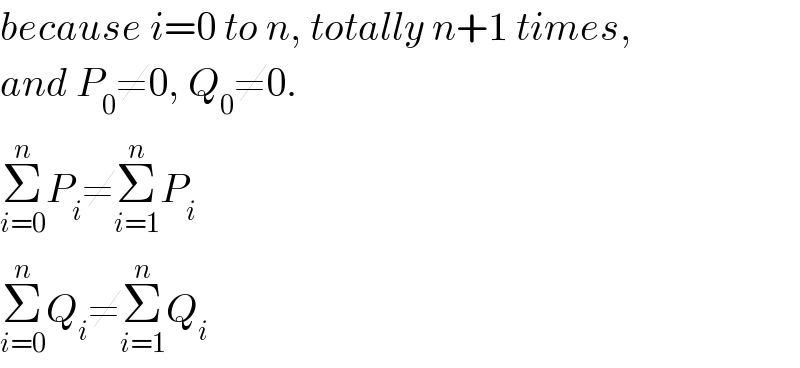
because i=0 to n, totally n+1 times, and P_0 ≠0, Q_0 ≠0. Σ_(i=0) ^n P_i ≠Σ_(i=1) ^n P_i Σ_(i=0) ^n Q_i ≠Σ_(i=1) ^n Q_i

$${because}\:{i}=\mathrm{0}\:{to}\:{n},\:{totally}\:{n}+\mathrm{1}\:{times}, \\ $$$${and}\:{P}_{\mathrm{0}} \neq\mathrm{0},\:{Q}_{\mathrm{0}} \neq\mathrm{0}. \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{P}_{{i}} \neq\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{P}_{{i}} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{Q}_{{i}} \neq\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{Q}_{{i}} \\ $$

Answered by mathmax by abdo last updated on 13/Jun/20

v_n =u_(n ) +6 ⇒v_(n+1) =u_(n+1) +6 =(1/2)u_n −3 +6 =(1/2)u_n +3 =(1/2)(u_n +6) =(1/2)v_n ⇒v_n is g.prog. ⇒v_n =v_0 ((1/2))^n we have v_0 =u_0 +6 =15 ⇒ v_n =((15)/2^n ) we have P_n =Σ_(i=0) ^n v_i =v_0 ×((1−q^(n+1) )/(1−q)) =15×((1−(1/2^(n+1) ))/(1/2)) =15(2−(2/2^(n+1) )) =15(2−(1/2^n )) ⇒P_n =30−((15)/2^n ) Q_n =Σ_(i=0) ^n u_i =Σ_(i=0) ^n (v_i −6) =Σ_(i=0) ^n v_i −6(n+1) =30−((15)/2^n )−6(n+1) ⇒lim_(n→+∞) Q_n =−∞

$$\mathrm{v}_{\mathrm{n}} =\mathrm{u}_{\mathrm{n}\:} +\mathrm{6}\:\Rightarrow\mathrm{v}_{\mathrm{n}+\mathrm{1}} \:=\mathrm{u}_{\mathrm{n}+\mathrm{1}} +\mathrm{6}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}_{\mathrm{n}} −\mathrm{3}\:+\mathrm{6}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}_{\mathrm{n}} +\mathrm{3}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{u}_{\mathrm{n}} +\mathrm{6}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{v}_{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{v}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{g}.\mathrm{prog}.\:\Rightarrow\mathrm{v}_{\mathrm{n}} =\mathrm{v}_{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}} \:\:\mathrm{we}\:\mathrm{have}\:\mathrm{v}_{\mathrm{0}} =\mathrm{u}_{\mathrm{0}} \:+\mathrm{6}\:=\mathrm{15}\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{n}} =\frac{\mathrm{15}}{\mathrm{2}^{\mathrm{n}} }\:\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{P}_{\mathrm{n}} =\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{v}_{\mathrm{i}} =\mathrm{v}_{\mathrm{0}} ×\frac{\mathrm{1}−\mathrm{q}^{\mathrm{n}+\mathrm{1}} }{\mathrm{1}−\mathrm{q}}\:=\mathrm{15}×\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }}{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{15}\left(\mathrm{2}−\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }\right)\:=\mathrm{15}\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\right)\:\Rightarrow\mathrm{P}_{\mathrm{n}} =\mathrm{30}−\frac{\mathrm{15}}{\mathrm{2}^{\mathrm{n}} } \\ $$$$\mathrm{Q}_{\mathrm{n}} =\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{u}_{\mathrm{i}} =\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \left(\mathrm{v}_{\mathrm{i}} −\mathrm{6}\right)\:=\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{v}_{\mathrm{i}} −\mathrm{6}\left(\mathrm{n}+\mathrm{1}\right) \\ $$$$=\mathrm{30}−\frac{\mathrm{15}}{\mathrm{2}^{\mathrm{n}} }−\mathrm{6}\left(\mathrm{n}+\mathrm{1}\right)\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\mathrm{Q}_{\mathrm{n}} =−\infty \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com