
Question and Answers Forum
Question Number 98416 by 175 last updated on 13/Jun/20

Answered by Farruxjano last updated on 13/Jun/20
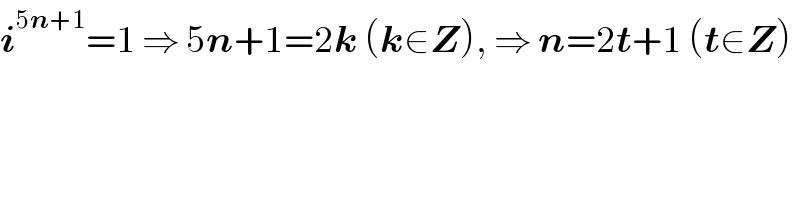
Answered by Ramajunan last updated on 13/Jun/20
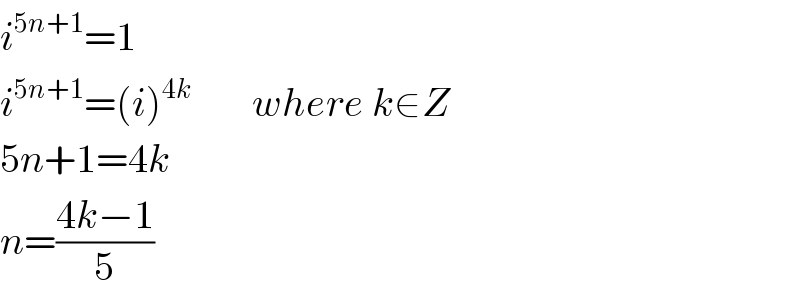
Answered by mathmax by abdo last updated on 13/Jun/20
![i^(5n+1) =1 ⇒(e^((iπ)/2) )^(5n+1) =e^(i2kπ) ⇒ e^(i(5n+1)(π/2)) =e^(i2kπ ) ⇒(5n+1)(π/2)=2kπ ⇒ 5n+1 =4k ⇒5n =4k−1 let use congruence modul 5(prime) ⇒ 4k^− −1^− =0 ⇒−k^− −1 =0 [5] ⇒k =4 [5] ⇒k =5p+4 ⇒ 5n =20p+16−1 ⇒5n =20p+15 ⇒n =4p+3 so all number at form 4p+3 is solution](Q98422.png)
| ||
Question and Answers Forum | ||
Question Number 98416 by 175 last updated on 13/Jun/20 | ||
 | ||
Answered by Farruxjano last updated on 13/Jun/20 | ||
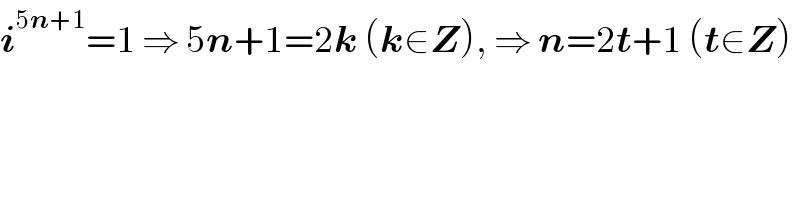 | ||
| ||
Answered by Ramajunan last updated on 13/Jun/20 | ||
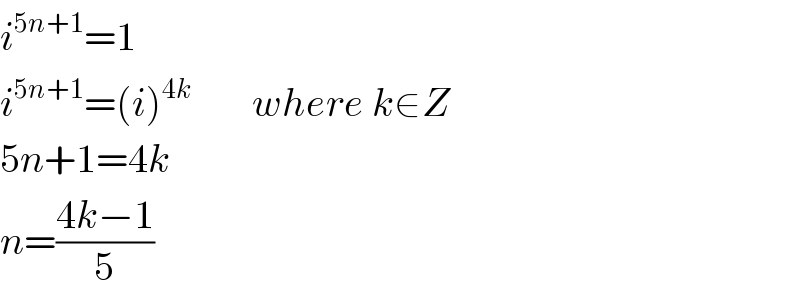 | ||
| ||
Answered by mathmax by abdo last updated on 13/Jun/20 | ||
![i^(5n+1) =1 ⇒(e^((iπ)/2) )^(5n+1) =e^(i2kπ) ⇒ e^(i(5n+1)(π/2)) =e^(i2kπ ) ⇒(5n+1)(π/2)=2kπ ⇒ 5n+1 =4k ⇒5n =4k−1 let use congruence modul 5(prime) ⇒ 4k^− −1^− =0 ⇒−k^− −1 =0 [5] ⇒k =4 [5] ⇒k =5p+4 ⇒ 5n =20p+16−1 ⇒5n =20p+15 ⇒n =4p+3 so all number at form 4p+3 is solution](Q98422.png) | ||
| ||