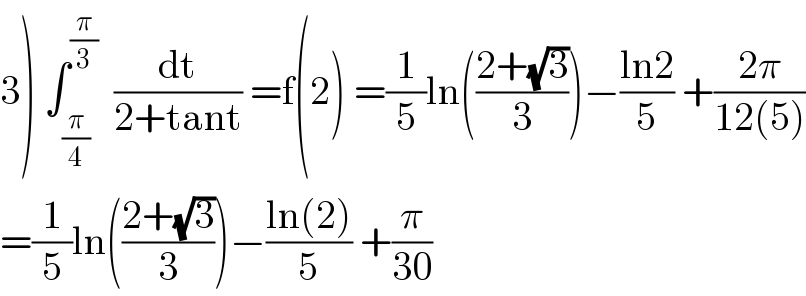let f(x) =∫_(π/4) ^(π/3) (dt/(x+tant)) calculate f(x) 2)explicit g(x) =∫_(π/4) ^(π/3) (dt/((x+tant)^2 )) 3) find the value of integrals ∫_(π/4) ^(π/3) (dt/(2+tant)) and ∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 98426 by mathmax by abdo last updated on 13/Jun/20

$let f (x) = \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{dt}{x + tant} calculate f (x)$ $2) explicit g (x) = \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{dt}{{(x + tant)}^{2}}$ $3) find the value of integrals \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{dt}{2 + tant} and \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{dt}{{(2 + tant)}^{2}}$
	Answered by maths mind last updated on 14/Jun/20
	$f(x)=∫_1 ^(√3) (dy/((x+y)(1+y^2 ))) =(1/(1+x^2 ))∫_1 ^(√3) (((x+y)(x−y)+1+y^2 )/((x+y)(1+y^2 )))dy =(1/(1+x^2 ))∫_1 ^(√3) {(x/(1+y^2 ))−(y/(1+y^2 ))+(1/(x+y))}dy =(x/(1+x^2 ))[(π/(12))]−((ln(2))/(2(1+x^2 )))+((ln(((x+(√3))/(x+1))))/((1+x^2 ))) g(x)=−f′(x) =−{((1−x^2 )/((1+x^2 )^2 ))(π/(12))+((xln(2))/((1+x^2 )^2 ))+(1/((1+x^2 )))[(1/(x+(√3)))−(1/(x+1))]−((2xln(((x+(√3))/(x+1))))/((1+x^2 )^2 ))} 3 ∫(dx/(2+tg(x)))=f(2)=(π/(30))−((ln(2))/(10))+((ln(((2+(√3))/3)))/5) ∫(dx/((2+tg(x))^2 ))=−{((−π)/(100)).+((2ln(2))/(25))+(1/5)((1/(2+(√3)))−(1/3))−((4ln(((2+(√3))/3)))/(25))}$
	$f (x) = \int_{1}^{\sqrt{3}} \frac{d y}{(x + y) (1 + y^{2})}$ $= \frac{1}{1 + x^{2}} \int_{1}^{\sqrt{3}} \frac{(x + y) (x - y) + 1 + y^{2}}{(x + y) (1 + y^{2})} d y$ $= \frac{1}{1 + x^{2}} \int_{1}^{\sqrt{3}} {\frac{x}{1 + y^{2}} - \frac{y}{1 + y^{2}} + \frac{1}{x + y}} d y$ $= \frac{x}{1 + x^{2}} [\frac{π}{12}] - \frac{l n (2)}{2 (1 + x^{2})} + \frac{l n (\frac{x + \sqrt{3}}{x + 1})}{(1 + x^{2})}$ $g (x) = - f^{'} (x)$ $= - {\frac{1 - x^{2}}{{(1 + x^{2})}^{2}} \frac{π}{12} + \frac{x l n (2)}{{(1 + x^{2})}^{2}} + \frac{1}{(1 + x^{2})} [\frac{1}{x + \sqrt{3}} - \frac{1}{x + 1}] - \frac{2 x l n (\frac{x + \sqrt{3}}{x + 1})}{{(1 + x^{2})}^{2}}}$ $3 \int \frac{d x}{2 + t g (x)} = f (2) = \frac{π}{30} - \frac{l n (2)}{10} + \frac{l n (\frac{2 + \sqrt{3}}{3})}{5}$ $\int \frac{d x}{{(2 + t g (x))}^{2}} = - {\frac{- π}{100} . + \frac{2 l n (2)}{25} + \frac{1}{5} (\frac{1}{2 + \sqrt{3}} - \frac{1}{3}) - \frac{4 l n (\frac{2 + \sqrt{3}}{3})}{25}}$
	Commented by abdomathmax last updated on 14/Jun/20

	$thanks sir .$
	Commented by maths mind last updated on 14/Jun/20

	$w i t h e p l e a s e r$
	Answered by abdomathmax last updated on 14/Jun/20
	$1) f(x) =∫_(π/4) ^(π/3) (dt/(x+tant)) changement tant =u give f(x) =∫_1 ^(√3) (du/((1+u^2 )(x+u))) let decompose F(u) =(1/((u+x)(u^2 +1))) ⇒F(u) =(a/(u+x)) +((bu +c)/(u^2 +1)) a =(1/(x^2 +1)) lim_(u→+∞) uF(u) =0 =a+b ⇒b=−(1/(x^2 +1)) F(0) =(1/x) =(a/x) +c ⇒1 =a+xc ⇒xc =1−a =1−(1/(x^2 +1)) =(x^2 /(1+x^2 )) ⇒c =(x/(1+x^2 )) ⇒ F(u) =(1/((x^2 +1)(u+x))) +((−(1/(x^2 +1))u +(x/(1+x^2 )))/(u^2 +1)) ⇒f(x) =(1/(x^2 +1)) ∫_1 ^(√3) (du/(u+x)) −(1/(x^2 +1)) ∫_1 ^(√3) ((u−x)/(u^2 +1)) du =(1/(x^2 +1))[ln∣u+x∣]_1 ^(√3) −(1/(2(x^2 +1))) [ln(u^2 +1)]_1 ^(√3) +(x/(x^2 +1)) [arctanu]_1 ^(√3) =(1/(x^2 +1)){ln∣(√3)+x∣−ln∣1+x∣} −((2ln(2))/(2(x^2 +1))) +(x/(x^2 +1))×(π/(12)) =(1/(x^2 +1))ln∣((x+(√3))/(x+1))∣−((ln2)/(x^2 +1)) +((πx)/(12(x^2 +1)))$
	$1) f (x) = \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{dt}{x + tant} changement tant = u give$ $f (x) = \int_{1}^{\sqrt{3}} \frac{du}{(1 + u^{2}) (x + u)} let decompose$ $F (u) = \frac{1}{(u + x) (u^{2} + 1)} \Rightarrow F (u) = \frac{a}{u + x} + \frac{bu + c}{u^{2} + 1}$ $a = \frac{1}{x^{2} + 1} \lim_{u \to + \infty} uF (u) = 0 = a + b \Rightarrow b = - \frac{1}{x^{2} + 1}$ $F (0) = \frac{1}{x} = \frac{a}{x} + c \Rightarrow 1 = a + xc \Rightarrow xc = 1 - a$ $= 1 - \frac{1}{x^{2} + 1} = \frac{x^{2}}{1 + x^{2}} \Rightarrow c = \frac{x}{1 + x^{2}} \Rightarrow$ $F (u) = \frac{1}{(x^{2} + 1) (u + x)} + \frac{- \frac{1}{x^{2} + 1} u + \frac{x}{1 + x^{2}}}{u^{2} + 1}$ $\Rightarrow f (x) = \frac{1}{x^{2} + 1} \int_{1}^{\sqrt{3}} \frac{du}{u + x}$ $- \frac{1}{x^{2} + 1} \int_{1}^{\sqrt{3}} \frac{u - x}{u^{2} + 1} du$ $= \frac{1}{x^{2} + 1} {[\ln ∣ u + x ∣]}_{1}^{\sqrt{3}} - \frac{1}{2 (x^{2} + 1)} {[\ln (u^{2} + 1)]}_{1}^{\sqrt{3}}$ $+ \frac{x}{x^{2} + 1} {[arctanu]}_{1}^{\sqrt{3}}$ $= \frac{1}{x^{2} + 1} {\ln ∣ \sqrt{3} + x ∣ - \ln ∣ 1 + x ∣}$ $- \frac{2 \ln (2)}{2 (x^{2} + 1)} + \frac{x}{x^{2} + 1} \times \frac{π}{12}$ $= \frac{1}{x^{2} + 1} \ln ∣ \frac{x + \sqrt{3}}{x + 1} ∣ - \frac{\ln 2}{x^{2} + 1} + \frac{π x}{12 (x^{2} + 1)}$
	Commented by abdomathmax last updated on 14/Jun/20
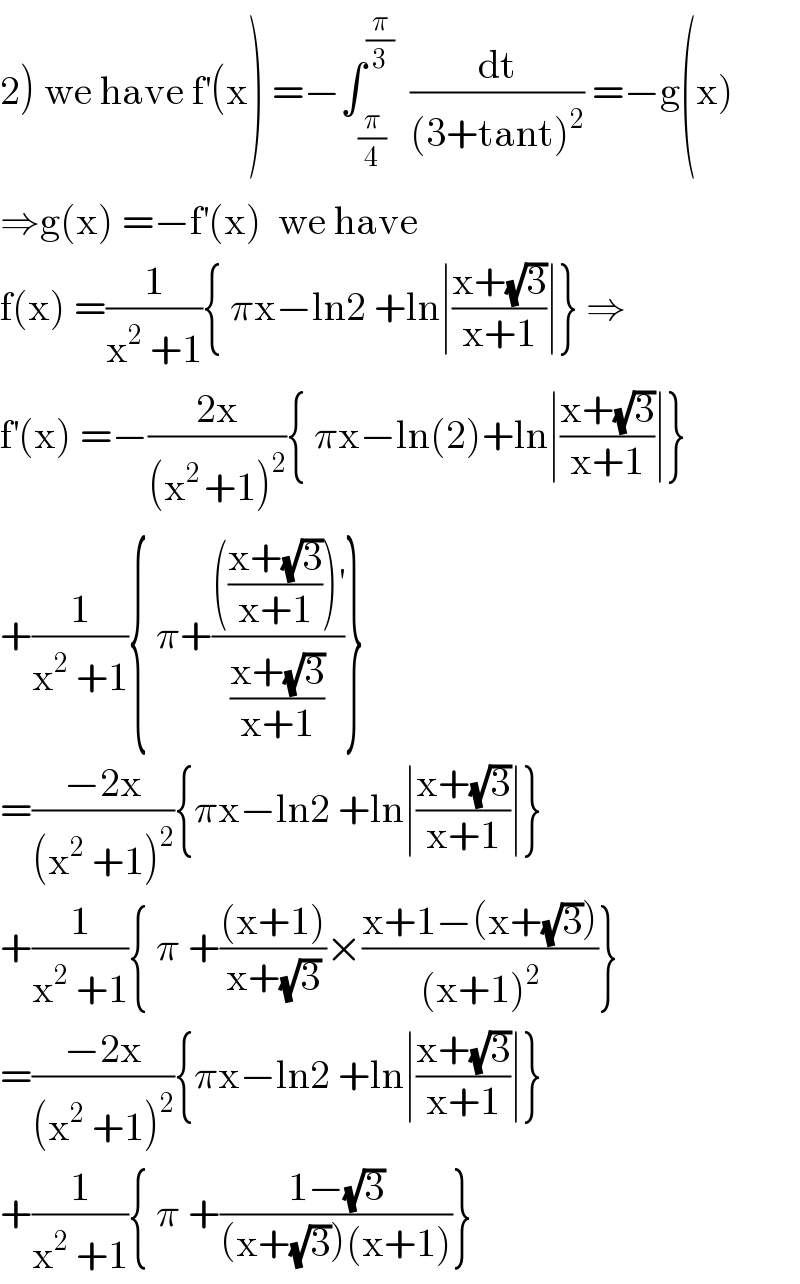
	$2) we have f^′ (x) =−∫_(π/4) ^(π/3) (dt/((3+tant)^2 )) =−g(x) ⇒g(x) =−f^′ (x) we have f(x) =(1/(x^2 +1)){ πx−ln2 +ln∣((x+(√3))/(x+1))∣} ⇒ f^′ (x) =−((2x)/((x^(2 ) +1)^2 )){ πx−ln(2)+ln∣((x+(√3))/(x+1))∣} +(1/(x^2 +1)){ π+(((((x+(√3))/(x+1)))^′ )/((x+(√3))/(x+1)))} =((−2x)/((x^2 +1)^2 )){πx−ln2 +ln∣((x+(√3))/(x+1))∣} +(1/(x^2 +1)){ π +(((x+1))/(x+(√3)))×((x+1−(x+(√3)))/((x+1)^2 ))} =((−2x)/((x^2 +1)^2 )){πx−ln2 +ln∣((x+(√3))/(x+1))∣} +(1/(x^2 +1)){ π +((1−(√3))/((x+(√3))(x+1)))}$
	$2) we have f^{^{'}} (x) = - \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{dt}{{(3 + tant)}^{2}} = - g (x)$ $\Rightarrow g (x) = - f^{^{'}} (x) we have$ $f (x) = \frac{1}{x^{2} + 1} {π x - \ln 2 + \ln ∣ \frac{x + \sqrt{3}}{x + 1} ∣} \Rightarrow$ $f^{^{'}} (x) = - \frac{2 x}{{(x^{2} + 1)}^{2}} {π x - \ln (2) + \ln ∣ \frac{x + \sqrt{3}}{x + 1} ∣}$ $+ \frac{1}{x^{2} + 1} {π + \frac{{(\frac{x + \sqrt{3}}{x + 1})}^{^{'}}}{\frac{x + \sqrt{3}}{x + 1}}}$ $= \frac{- 2 x}{{(x^{2} + 1)}^{2}} {π x - \ln 2 + \ln ∣ \frac{x + \sqrt{3}}{x + 1} ∣}$ $+ \frac{1}{x^{2} + 1} {π + \frac{(x + 1)}{x + \sqrt{3}} \times \frac{x + 1 - (x + \sqrt{3})}{{(x + 1)}^{2}}}$ $= \frac{- 2 x}{{(x^{2} + 1)}^{2}} {π x - \ln 2 + \ln ∣ \frac{x + \sqrt{3}}{x + 1} ∣}$ $+ \frac{1}{x^{2} + 1} {π + \frac{1 - \sqrt{3}}{(x + \sqrt{3}) (x + 1)}}$
	Commented by mathmax by abdo last updated on 14/Jun/20
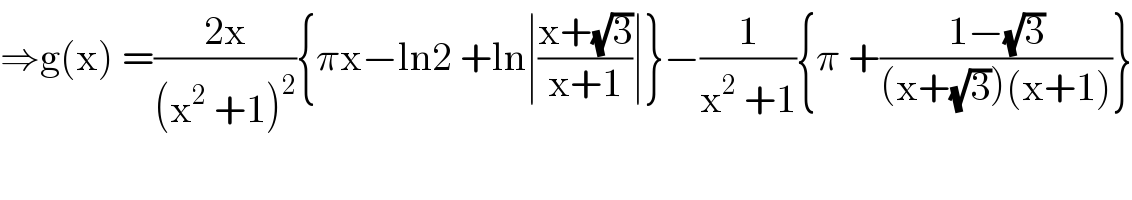
	$⇒g(x) =((2x)/((x^2 +1)^2 )){πx−ln2 +ln∣((x+(√3))/(x+1))∣}−(1/(x^2 +1)){π +((1−(√3))/((x+(√3))(x+1)))}$
	$\Rightarrow g (x) = \frac{2 x}{{(x^{2} + 1)}^{2}} {π x - \ln 2 + \ln ∣ \frac{x + \sqrt{3}}{x + 1} ∣} - \frac{1}{x^{2} + 1} {π + \frac{1 - \sqrt{3}}{(x + \sqrt{3}) (x + 1)}}$
	Commented by mathmax by abdo last updated on 14/Jun/20

	$3) \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{dt}{2 + tant} = f (2) = \frac{1}{5} \ln (\frac{2 + \sqrt{3}}{3}) - \frac{\ln 2}{5} + \frac{2 π}{12 (5)}$ $= \frac{1}{5} \ln (\frac{2 + \sqrt{3}}{3}) - \frac{\ln (2)}{5} + \frac{π}{30}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum