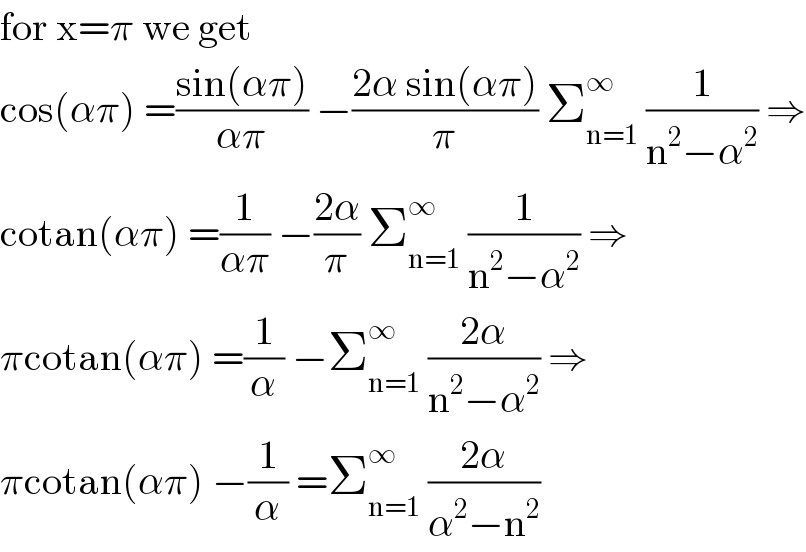Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 98429 by mathmax by abdo last updated on 13/Jun/20

Answered by abdomathmax last updated on 15/Jun/20
![f is even ⇒f(x) =(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) a_n =(2/T)∫_([T]) f(x)cos(nx)dx =(1/π)∫_(−π) ^π cos(αx)cos(nx)dx =(2/π) ∫_0 ^π cos(αx)cos(nx)dx ⇒ (π/2)a_n =(1/2) ∫_0 ^π {cos(n+α)x+cos(n−α)x}dx ⇒πa_n =[(1/(n+α))sin(n+α)x+(1/(n−α)) sin(n−α)x]_0 ^π =(1/(n+α)) sin(nπ +απ)+(1/(n−α))sin(nπ−απ) =(((−1)^n sin(απ))/(n+α))−(((−1)^n sin(απ))/(n−α)) =(−1)^n sin(απ){(1/(n+α))−(1/(n−α))} =(−1)^n sin(απ)(((−2α)/(n^2 −α^2 ))) (but α ∈ R−Z) ⇒ a_n =−2α ((sin(απ))/(π(n^2 −α^2 )))(−1)^n a_0 =((2sin(απ))/(απ)) ⇒ cos(αx) =((sin(απ))/(απ)) −((2sin(απ))/π)Σ_(n=1) ^∞ (((−1)^n )/(n^2 −α^2 ))cos(nx)](Q98668.png)
Commented by abdomathmax last updated on 15/Jun/20
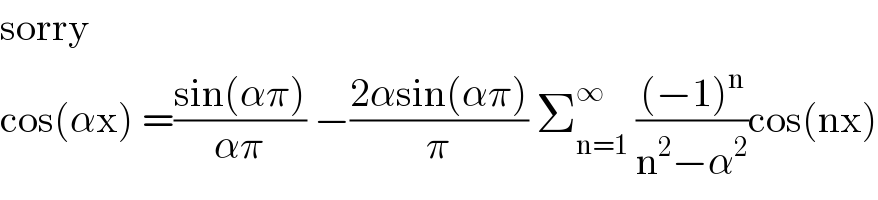
Commented by abdomathmax last updated on 15/Jun/20