
Question Number 98443 by Ar Brandon last updated on 14/Jun/20
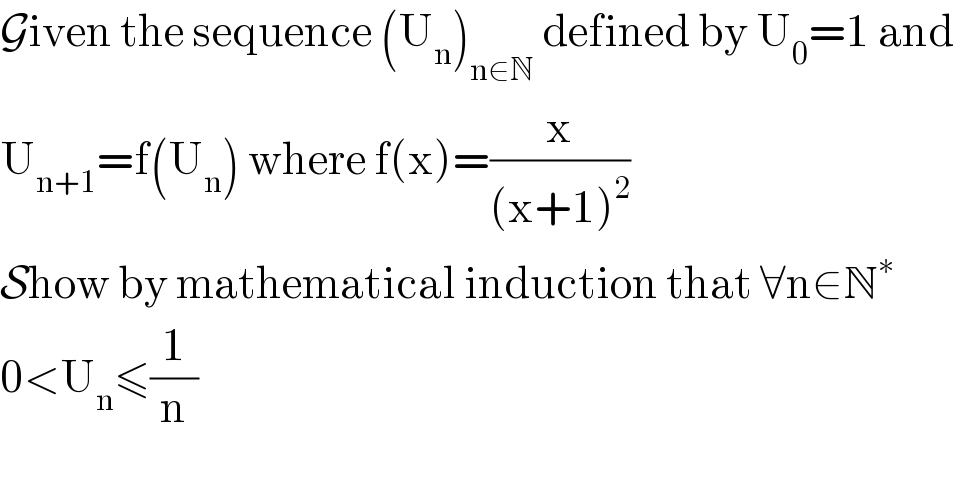
$$\mathcal{G}\mathrm{iven}\:\mathrm{the}\:\mathrm{sequence}\:\left(\mathrm{U}_{\mathrm{n}} \right)_{\mathrm{n}\in\mathbb{N}} \:\mathrm{defined}\:\mathrm{by}\:\mathrm{U}_{\mathrm{0}} =\mathrm{1}\:\mathrm{and} \\ $$ $$\mathrm{U}_{\mathrm{n}+\mathrm{1}} =\mathrm{f}\left(\mathrm{U}_{\mathrm{n}} \right)\:\mathrm{where}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$ $$\mathcal{S}\mathrm{how}\:\mathrm{by}\:\mathrm{mathematical}\:\mathrm{induction}\:\mathrm{that}\:\forall\mathrm{n}\in\mathbb{N}^{\ast} \\ $$ $$\mathrm{0}<\mathrm{U}_{\mathrm{n}} \leqslant\frac{\mathrm{1}}{\mathrm{n}} \\ $$
Answered by maths mind last updated on 14/Jun/20
![f(x)=(1/(x+1))−(1/((x+1)^2 )) f′(x)=−(1/((x+1)^2 ))+(2/((x+1)^3 ))=((1−x)/((1+x)^3 ))≥0 ,∀x∈[0,1] 0<U_0 =1≤1 true we assume That ∀n∈N 0<U_n ≤(1/n)≤1 since f is increasing over [0,1]⇒ ⇒f(0)<f(u_n )≤f((1/n)) ⇔0<U_(n+1) ≤(n/((n+1)^2 ))=(n/(n+1)).(1/(n+1))≤1.(1/(n+1))=(1/(n+1)) ⇒∀n∈N 0<U_n ≤(1/n)](Q98497.png)
$${f}\left({x}\right)=\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $${f}'\left({x}\right)=−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{1}−{x}}{\left(\mathrm{1}+{x}\right)^{\mathrm{3}} }\geqslant\mathrm{0}\:,\forall{x}\in\left[\mathrm{0},\mathrm{1}\right] \\ $$ $$\mathrm{0}<{U}_{\mathrm{0}} =\mathrm{1}\leqslant\mathrm{1}\:{true} \\ $$ $${we}\:{assume}\:{That}\:\forall{n}\in\mathbb{N}\:\mathrm{0}<{U}_{{n}} \leqslant\frac{\mathrm{1}}{{n}}\leqslant\mathrm{1} \\ $$ $${since}\:{f}\:{is}\:{increasing}\:{over}\:\left[\mathrm{0},\mathrm{1}\right]\Rightarrow \\ $$ $$\Rightarrow{f}\left(\mathrm{0}\right)<{f}\left({u}_{{n}} \right)\leqslant{f}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$ $$\Leftrightarrow\mathrm{0}<{U}_{{n}+\mathrm{1}} \leqslant\frac{{n}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{{n}}{{n}+\mathrm{1}}.\frac{\mathrm{1}}{{n}+\mathrm{1}}\leqslant\mathrm{1}.\frac{\mathrm{1}}{{n}+\mathrm{1}}=\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$ $$\Rightarrow\forall{n}\in\mathbb{N}\:\:\:\:\mathrm{0}<{U}_{{n}} \leqslant\frac{\mathrm{1}}{{n}} \\ $$
Commented byAr Brandon last updated on 14/Jun/20
Thank you ��
