
Question and Answers Forum
Question Number 98448 by Quvonchbek last updated on 14/Jun/20

Commented by Rasheed.Sindhi last updated on 14/Jun/20
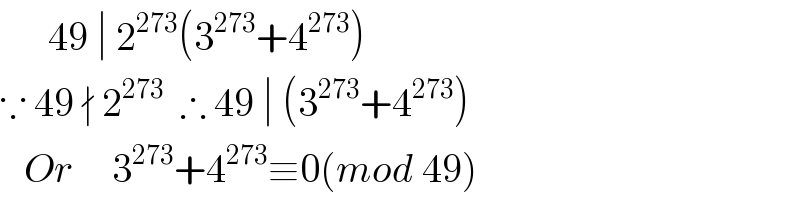
Commented by mr W last updated on 14/Jun/20
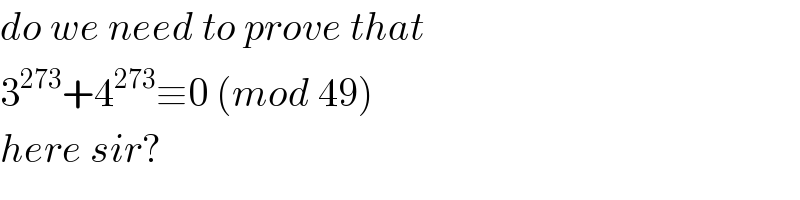
Commented by Rasheed.Sindhi last updated on 14/Jun/20
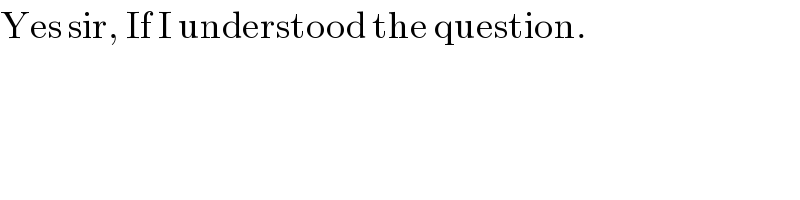
Commented by 1549442205 last updated on 14/Jun/20

Commented by mr W last updated on 14/Jun/20
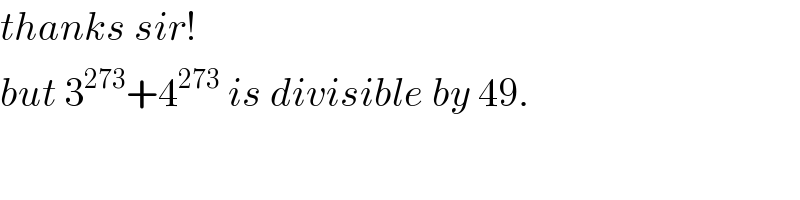
Answered by Rasheed.Sindhi last updated on 14/Jun/20
![6^(273) +8^(273) ≡0(mod 49) ⇒2^(273) (3^(273) +4^(273) )≡0(mod 49) ⇒(3^(273) +4^(273) )≡0(mod 49) [∵ 49∤2^(273) ] ^• 4^(21) ≡1(mod 49) (4^(21) )^(13) ≡(1)^(13) (mod 49) 4^(273) ≡1(mod 49)............(i) ^• 3^(42) ≡1(mod 49) (3^(42) )^6 ≡(1)^6 (mod 49) 3^(252) ≡1(mod 49) 3^(252) .3^(21) ≡1.3^(21) ≡48(mod 49) 3^(273) ≡48(mod 49)...........(ii) (i)+(ii): 3^(273) +4^(273) ≡49≡0(mod49) 3^(273) +4^(273) ≡0(mod49) Proved](Q98511.png)
Commented by mr W last updated on 14/Jun/20

