
Question and Answers Forum
Question Number 98537 by student work last updated on 14/Jun/20
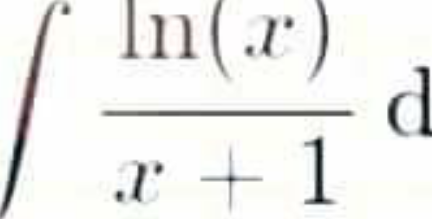
Commented by student work last updated on 14/Jun/20

Answered by mathmax by abdo last updated on 14/Jun/20
![at form of serie I =∫ ((lnx)/(1+x))dx let f(x) =∫_0 ^x ((ln(t))/(1+t)) dt (x>0) case 1 o<x<1 ⇒f(x) =∫_0 ^x ln(t)Σ_(n=0) ^∞ (−1)^n t^n dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^x t^n ln(t) dt =Σ_(n=0) ^∞ (−1)^n A_n by parts A_n =[(t^(n+1) /(n+1))ln(t)]_0 ^x −∫_0 ^x (t^n /(n+1)) dt =(x^(n+1) /(n+1))lnx−(x^(n+1) /((n+1)^2 )) ⇒ I =Σ_(n=0) ^∞ (((−1)^n )/(n+1)) x^(n+1) ln(x)−Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) x^(n+1) case 2 x>1 ⇒(1/x)<1 we do the changement t=(1/u) ⇒ f(x) =∫_0 ^1 ((ln(t))/(1+t))dt +∫_1 ^x ((ln(t))/(1+t)) dt(→t=(1/u)) =∫_0 ^1 ((ln(t))/(1+t))dt −∫_(1/x) ^1 ((−lnu)/(1+(1/u)))×((−du)/u^2 ) =∫_0 ^1 ((ln(t))/(1+t))dt −∫_(1/x) ^1 ((lnu)/(1+u^2 ))du =∫_0 ^1 ln(t)Σ_(n=0) ^∞ (−1)^n t^n dt −∫_(1/x) ^1 lnt(Σ_(n=0) ^∞ (−1)^n t^(2n) )dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 t^n lnt dt −Σ_(n=0) ^∞ (−1)^n ∫_(1/x) ^1 t^(2n) lnt dt ∫_0 ^1 t^n ln(t)dt =[(t^(n+1) /(n+1))lnt]_0 ^1 −∫_0 ^1 (t^n /(n+1)) dt =−(1/((n+1)^2 )) ⇒ ∫_0 ^1 ((lnt)/(1+t))dt =Σ_(n=0) ^∞ (((−1)^(n+1) )/((n+1)^2 )) =Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =(2^(1−2) −1)ξ(2) =−(π^2 /(12)) ∫_(1/x) ^1 t^(2n) ln(t)dt =[(t^(2n+1) /(2n+1)) ln(t)]_(1/x) ^1 −∫_(1/x) ^1 (t^(2n) /(2n+1))dt =((ln(x))/((2n+1)x^(2n+1) )) −(1/((2n+1)^2 ))(1−(1/x^(2n+1) )) ⇒ ∫_(1/x) ^1 ((lnu)/(1+u^2 ))du =Σ_(n=0) ^∞ (((−1)^n ln(x))/((2n+1)x^(2n+1) )) −Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))(→k catalan constant) +Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 x^(2n+1) ))](Q98555.png)
| ||
Question and Answers Forum | ||
Question Number 98537 by student work last updated on 14/Jun/20 | ||
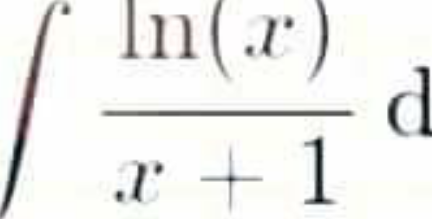 | ||
Commented by student work last updated on 14/Jun/20 | ||
 | ||
Answered by mathmax by abdo last updated on 14/Jun/20 | ||
![at form of serie I =∫ ((lnx)/(1+x))dx let f(x) =∫_0 ^x ((ln(t))/(1+t)) dt (x>0) case 1 o<x<1 ⇒f(x) =∫_0 ^x ln(t)Σ_(n=0) ^∞ (−1)^n t^n dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^x t^n ln(t) dt =Σ_(n=0) ^∞ (−1)^n A_n by parts A_n =[(t^(n+1) /(n+1))ln(t)]_0 ^x −∫_0 ^x (t^n /(n+1)) dt =(x^(n+1) /(n+1))lnx−(x^(n+1) /((n+1)^2 )) ⇒ I =Σ_(n=0) ^∞ (((−1)^n )/(n+1)) x^(n+1) ln(x)−Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) x^(n+1) case 2 x>1 ⇒(1/x)<1 we do the changement t=(1/u) ⇒ f(x) =∫_0 ^1 ((ln(t))/(1+t))dt +∫_1 ^x ((ln(t))/(1+t)) dt(→t=(1/u)) =∫_0 ^1 ((ln(t))/(1+t))dt −∫_(1/x) ^1 ((−lnu)/(1+(1/u)))×((−du)/u^2 ) =∫_0 ^1 ((ln(t))/(1+t))dt −∫_(1/x) ^1 ((lnu)/(1+u^2 ))du =∫_0 ^1 ln(t)Σ_(n=0) ^∞ (−1)^n t^n dt −∫_(1/x) ^1 lnt(Σ_(n=0) ^∞ (−1)^n t^(2n) )dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 t^n lnt dt −Σ_(n=0) ^∞ (−1)^n ∫_(1/x) ^1 t^(2n) lnt dt ∫_0 ^1 t^n ln(t)dt =[(t^(n+1) /(n+1))lnt]_0 ^1 −∫_0 ^1 (t^n /(n+1)) dt =−(1/((n+1)^2 )) ⇒ ∫_0 ^1 ((lnt)/(1+t))dt =Σ_(n=0) ^∞ (((−1)^(n+1) )/((n+1)^2 )) =Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =(2^(1−2) −1)ξ(2) =−(π^2 /(12)) ∫_(1/x) ^1 t^(2n) ln(t)dt =[(t^(2n+1) /(2n+1)) ln(t)]_(1/x) ^1 −∫_(1/x) ^1 (t^(2n) /(2n+1))dt =((ln(x))/((2n+1)x^(2n+1) )) −(1/((2n+1)^2 ))(1−(1/x^(2n+1) )) ⇒ ∫_(1/x) ^1 ((lnu)/(1+u^2 ))du =Σ_(n=0) ^∞ (((−1)^n ln(x))/((2n+1)x^(2n+1) )) −Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))(→k catalan constant) +Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 x^(2n+1) ))](Q98555.png) | ||
| ||