Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 98539 by Rio Michael last updated on 14/Jun/20

$$\mathrm{Given}\mathrm{the}\mathrm{function}$$$$f\left(x\right)=\frac{\ln x}{x-1}$$$$\left(\mathrm{a}\right)\mathrm{State}\mathrm{the}\mathrm{domain}{D}_f\mathrm{of}f.$$$$\left(\mathrm{b}\right)\mathrm{Find}\underset{x\to \mathrm{\infty }}{\lim }\frac{\ln x}{x-1}.\mathrm{State}\mathrm{its}\mathrm{asymptotes}.$$$$\left(\mathrm{c}\right)\mathrm{Draw}\mathrm{up}\mathrm{a}\mathrm{variation}\mathrm{table}\mathrm{for}\mathrm{the}\mathrm{curve}y=f\left(x\right).$$

Answered by Aziztisffola last updated on 14/Jun/20

$$\mathrm{a}){\mathrm{D}}_{\mathrm{f}}=]0;1[\cup ]1;+\mathrm{\infty }[$$$$\mathrm{b})\underset{x\to \mathrm{\infty }}{\lim f}\left(\mathrm{x}\right)=0$$

Commented by Rio Michael last updated on 14/Jun/20

$$\mathrm{great}\mathrm{sir},\mathrm{is}x=0\mathrm{an}\mathrm{asymptote}\mathrm{or}$$$$x=1??\mathrm{which}$$

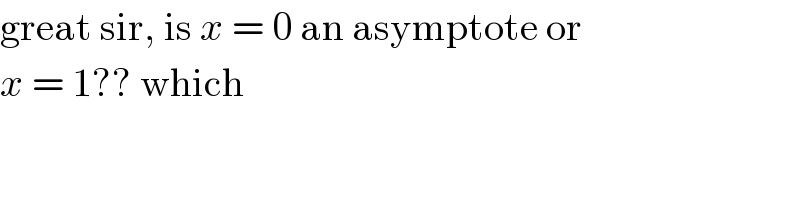
Commented by Aziztisffola last updated on 14/Jun/20

$$\mathrm{yes}\mathrm{x}=0\mathrm{and}\mathrm{x}=1$$

Answered by mathmax by abdo last updated on 14/Jun/20

$$1)\mathrm{f}\mathrm{is}\mathrm{defined}\mathrm{on}]0,1[\cup ]1,+\mathrm{\infty }[$$$$2){\lim }_{\mathrm{x}\to +\mathrm{\infty }}\frac{\mathrm{lnx}}{\mathrm{x}-1}={\lim }_{\mathrm{x}\to +\mathrm{\infty }}\frac{\mathrm{lnx}}{\mathrm{x}}\times \frac{1}{1-\frac{1}{\mathrm{x}}}={\lim }_{\mathrm{x}\to +\mathrm{\infty }}\frac{\mathrm{lnx}}{\mathrm{x}}=0\mathrm{so}\mathrm{y}=0\mathrm{is}$$$$\mathrm{assymptote}\mathrm{alway}\mathrm{x}=1\mathrm{is}\mathrm{assymtote}.$$$$3){\mathrm{f}}^{{}^{\prime }}\left(\mathrm{x}\right)=\frac{\frac{1}{\mathrm{x}}(\mathrm{x}-1)-\mathrm{lnx}}{{(\mathrm{x}-1)}^2}=\frac{(\mathrm{x}-1)-\mathrm{xlnx}}{\mathrm{x}{(\mathrm{x}-1)}^2}=\frac{\phi \left(\mathrm{x}\right)}{\mathrm{x}{(\mathrm{x}-1)}^2}$$$$\phi \left(\mathrm{x}\right)=\mathrm{x}-1-\mathrm{xlnx}\Rightarrow {\phi }^{{}^{\prime }}\left(\mathrm{x}\right)=1-(\mathrm{lnx}+1)=-\mathrm{lnx}$$$${\phi }^{{}^{\prime }}>0\iff -\mathrm{lnx}>0\iff \mathrm{lnx}<0\iff 0<\mathrm{x}<1$$$$\mathrm{x}01+\mathrm{\infty }$$$${\phi }^{{}^{\prime }}\mid \mid +-$$$$\phi \mid \mid -\mathrm{\infty }\mathrm{decr}0\mathrm{decr}-\mathrm{\infty }\Rightarrow \phi \left(\mathrm{x}\right)⩽0\Rightarrow {\mathrm{f}}^{{}^{\prime }}<0\Rightarrow \mathrm{f}\mathrm{is}\mathrm{strictly}\mathrm{ideccreazing}$$$$\mathrm{vareiation}\mathrm{of}\mathrm{f}$$$$\mathrm{x}01+\mathrm{\infty }{\lim }_{\mathrm{x}\to 1}\mathrm{f}\left(\mathrm{x}\right)=1$$$${\mathrm{f}}^{{}^{\prime }}\left(\mathrm{x}\right)\mid \mid -\mid \mid -$$$$\mathrm{f}\left(\mathrm{x}\right)\mid \mid +\mathrm{\infty }\mathrm{dec}1\mathrm{decr}0$$

Commented by Rio Michael last updated on 14/Jun/20

$$\mathrm{Brilliant}\mathrm{work}\mathrm{you}\mathrm{two}.$$$$\mathrm{thanks}$$

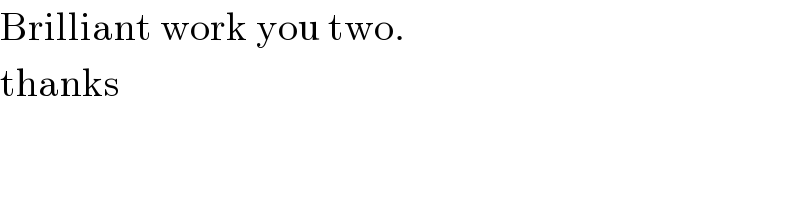
Commented by abdomathmax last updated on 15/Jun/20

$$\mathrm{you}\mathrm{are}\mathrm{welcome}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com