Question Number 98679 by M±th+et+s last updated on 15/Jun/20
$${prove}\:{that}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{3}+\mathrm{2}\sqrt{{x}}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}}{dx}=\mathrm{4}.\mathrm{13049}\: \\ $$
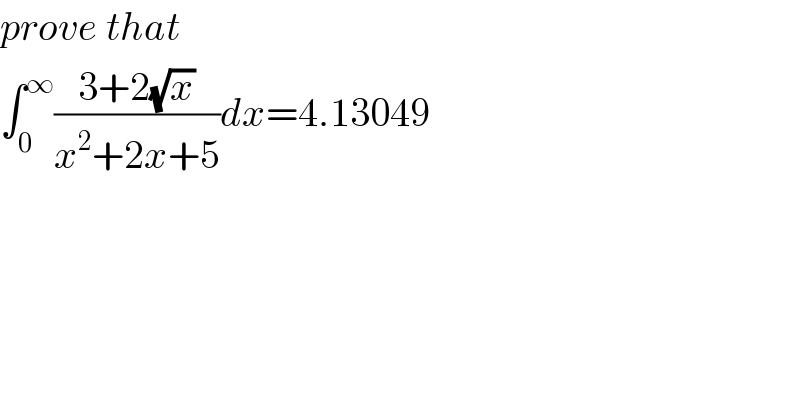
Commented by MJS last updated on 15/Jun/20
$${t}=\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}}{dt} \\ $$$$\mathrm{2}\int\frac{{t}\left(\mathrm{2}{t}+\mathrm{3}\right)}{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{5}}{dt} \\ $$$$\mathrm{now}\:\mathrm{decompose}\:\left(\mathrm{2}\:\mathrm{square}\:\mathrm{factors}\right)\:\mathrm{and}\:\mathrm{solve}. \\ $$$$\mathrm{as}\:\mathrm{many}\:\mathrm{times}\:\mathrm{before},\:\mathrm{easy}\:\mathrm{path}\:\mathrm{but}\:\mathrm{horrible} \\ $$$$\mathrm{constants}... \\ $$$$\mathrm{2}\int\frac{{t}\left(\mathrm{2}{t}+\mathrm{3}\right)}{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{5}}{dt}= \\ $$$$=\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\left(\int\frac{\mathrm{2}{t}+\mathrm{3}}{{t}^{\mathrm{2}} −\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{t}+\sqrt{\mathrm{5}}}{dt}−\right. \\ $$$$\left.\:\:\:\:\:−\int\frac{\mathrm{2}{t}+\mathrm{3}}{{t}^{\mathrm{2}} +\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{t}+\sqrt{\mathrm{5}}}{dt}\right)= \\ $$$$=\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}×\left(\right. \\ $$$$\:\:\:\:\:\int\frac{\mathrm{2}{t}−\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}}{{t}^{\mathrm{2}} −\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{t}+\sqrt{\mathrm{5}}}{dt}+ \\ $$$$\left.\:\:\:\:\:+\left(\mathrm{3}+\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}\right)\int\frac{{dt}}{{t}^{\mathrm{2}} −\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{t}+\sqrt{\mathrm{5}}}\right)− \\ $$$$\:\:\:\:\:−\int\frac{\mathrm{2}{t}+\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}}{{t}^{\mathrm{2}} +\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{t}+\sqrt{\mathrm{5}}}{dt}− \\ $$$$\:\:\:\:\:−\left(\mathrm{3}−\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}\right)\int\frac{{dt}}{{t}^{\mathrm{2}} +\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{t}+\sqrt{\mathrm{5}}} \\ $$$$\left.\right) \\ $$$$...\mathrm{and}\:\mathrm{tbese}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\left(\mathrm{I}\:\mathrm{hope}\:\mathrm{I}\:\mathrm{made}\:\mathrm{no}\:\mathrm{error}\:\mathrm{of}\:\mathrm{sign}\:\mathrm{in}\:\mathrm{front}\:\mathrm{of}\right. \\ $$$$\left.\mathrm{the}\:``\int''{s}...\right) \\ $$
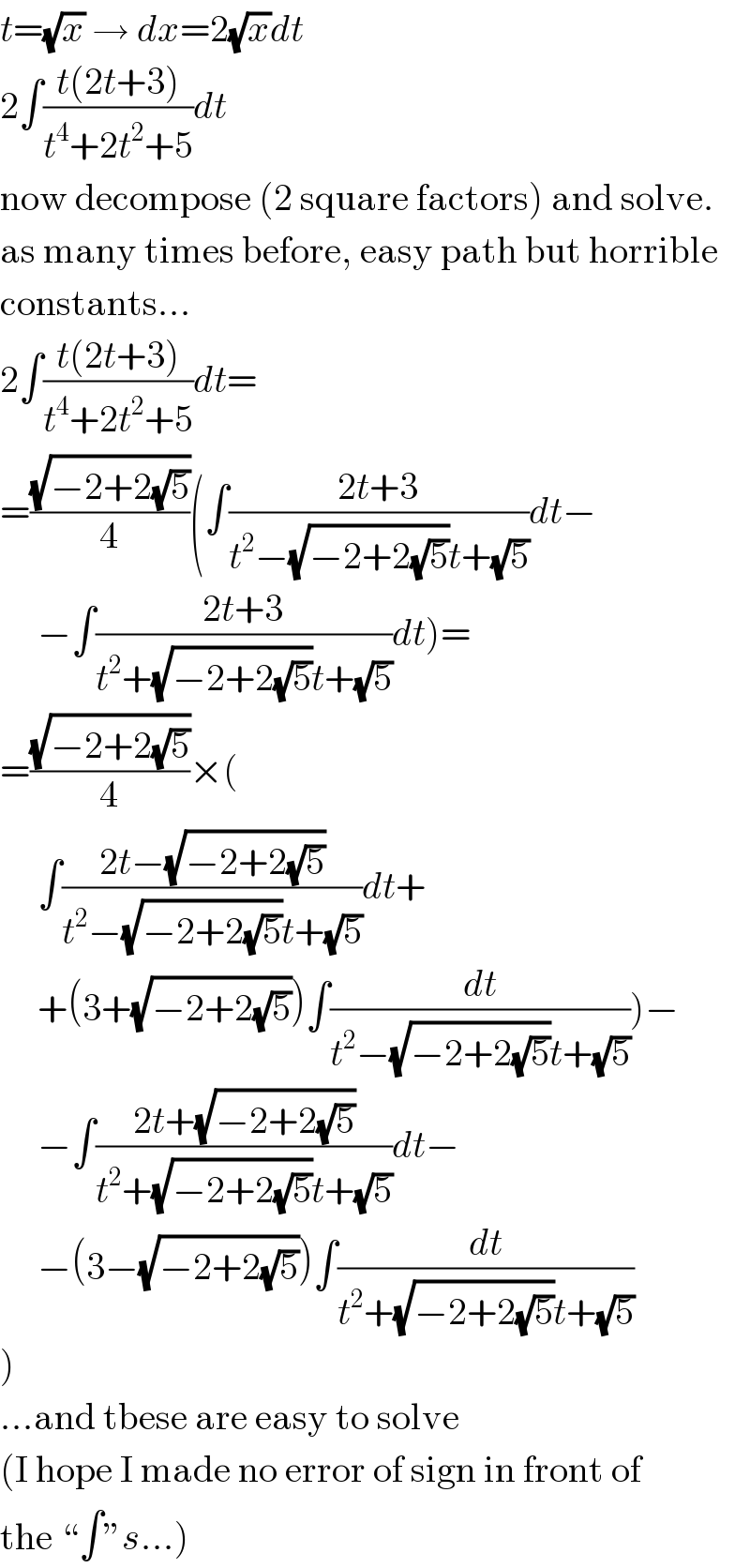
Commented by M±th+et+s last updated on 15/Jun/20
$${thank}\:{you}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 15/Jun/20
![I =∫_0 ^∞ ((3+2(√x))/(x^2 +2x+5)) dx changement (√x)=t give I =∫_0 ^∞ ((3+2t)/(t^4 +2t^(2 ) +5))(2t)dt =2 ∫_0 ^∞ ((3t+2t^2 )/(t^4 +2t^2 +5))dt let decompose F(t) =((2t^2 +3t)/(t^4 +2t^2 +5)) t^4 +2t^2 +5 =0 →u^2 +2u +5 =0 →Δ^′ =−4 ⇒u_1 =−1+2i and u_2 =−1−2i ⇒u^2 +2u +5 =(u−u_1 )(u−u_2 ) =(t^2 −u_1 )(t^2 −u_2 ) ⇒ I =∫_0 ^∞ ((2t^2 +3t)/((t^2 −u_1 )(t^2 −u_2 )))dt =(1/(4i))∫_0 ^∞ (2t^2 +3t)((1/(t^2 −u_1 ))−(1/(t^2 −u_2 )))dt =(1/(4i))∫_0 ^∞ ((2t^2 +3t)/(t^2 −u_1 )) dt−(1/(4i))∫_0 ^∞ ((2t^2 +3t)/(t^2 −u_2 ))dt =(1/(4i))∫_0 ^∞ ((2(t^2 −u_1 )+3t+2u_1 )/(t^2 −u_1 ))dt −(1/(4i))∫_0 ^∞ ((2(t^2 −u_2 )+3t+2u_2 )/(t^2 −u_2 ))dt =(1/(4i)){ ∫_0 ^∞ ((3t+2u_1 )/(t^2 −u_1 )) dt −∫_0 ^∞ ((3t+2u_2 )/(t^2 −u_2 ))dt} =(1/(4i)){ (3/2) [ln(((t^2 −u_1 )/(t^2 −u_2 )))]_0 ^(+∞) +2 ∫_0 ^∞ (u_1 /(t^2 −u_1 )) dt−2 ∫_0 ^∞ (u_2 /(t^2 −u_2 ))dt} =(3/(8i))ln((u_1 /u_2 )) +(1/(2i)){ u_1 ∫_0 ^∞ (dt/(t^2 −u_1 )) −u_2 ∫_0 ^∞ (dt/(t^2 −u_2 ))}....be continued...](Q98712.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{x}}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{5}}\:\mathrm{dx}\:\mathrm{changement}\:\sqrt{\mathrm{x}}=\mathrm{t}\:\mathrm{give}\: \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{3}+\mathrm{2t}}{\mathrm{t}^{\mathrm{4}} \:+\mathrm{2t}^{\mathrm{2}\:} +\mathrm{5}}\left(\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{3t}+\mathrm{2t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} \:+\mathrm{2t}^{\mathrm{2}} \:+\mathrm{5}}\mathrm{dt}\:\:\mathrm{let}\:\mathrm{decompose} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{2t}^{\mathrm{2}} \:+\mathrm{3t}}{\mathrm{t}^{\mathrm{4}} \:+\mathrm{2t}^{\mathrm{2}} \:+\mathrm{5}} \\ $$$$\mathrm{t}^{\mathrm{4}} \:+\mathrm{2t}^{\mathrm{2}} \:+\mathrm{5}\:=\mathrm{0}\:\rightarrow\mathrm{u}^{\mathrm{2}} \:+\mathrm{2u}\:+\mathrm{5}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:=−\mathrm{4}\:\Rightarrow\mathrm{u}_{\mathrm{1}} =−\mathrm{1}+\mathrm{2i}\:\mathrm{and}\:\mathrm{u}_{\mathrm{2}} =−\mathrm{1}−\mathrm{2i} \\ $$$$\Rightarrow\mathrm{u}^{\mathrm{2}} +\mathrm{2u}\:+\mathrm{5}\:=\left(\mathrm{u}−\mathrm{u}_{\mathrm{1}} \right)\left(\mathrm{u}−\mathrm{u}_{\mathrm{2}} \right)\:=\left(\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} \right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2t}^{\mathrm{2}} \:+\mathrm{3t}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} \right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} \right)}\mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{4i}}\int_{\mathrm{0}} ^{\infty} \left(\mathrm{2t}^{\mathrm{2}} \:+\mathrm{3t}\right)\left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4i}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2t}^{\mathrm{2}} \:+\mathrm{3t}}{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }\:\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{4i}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2t}^{\mathrm{2}} \:+\mathrm{3t}}{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4i}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} \right)+\mathrm{3t}+\mathrm{2u}_{\mathrm{1}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }\mathrm{dt}\:−\frac{\mathrm{1}}{\mathrm{4i}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} \right)+\mathrm{3t}+\mathrm{2u}_{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4i}}\left\{\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{3t}+\mathrm{2u}_{\mathrm{1}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }\:\mathrm{dt}\:−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{3t}+\mathrm{2u}_{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\mathrm{dt}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4i}}\left\{\:\frac{\mathrm{3}}{\mathrm{2}}\:\left[\mathrm{ln}\left(\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{+\infty} \:+\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{u}_{\mathrm{1}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }\:\mathrm{dt}−\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{u}_{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\mathrm{dt}\right\} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8i}}\mathrm{ln}\left(\frac{\mathrm{u}_{\mathrm{1}} }{\mathrm{u}_{\mathrm{2}} }\right)\:+\frac{\mathrm{1}}{\mathrm{2i}}\left\{\:\mathrm{u}_{\mathrm{1}} \int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }\:−\mathrm{u}_{\mathrm{2}} \int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\right\}....\mathrm{be}\:\mathrm{continued}... \\ $$
Commented by M±th+et+s last updated on 15/Jun/20
$${thanks}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 16/Jun/20
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}. \\ $$