
Question and Answers Forum
Question Number 98826 by bramlex last updated on 16/Jun/20
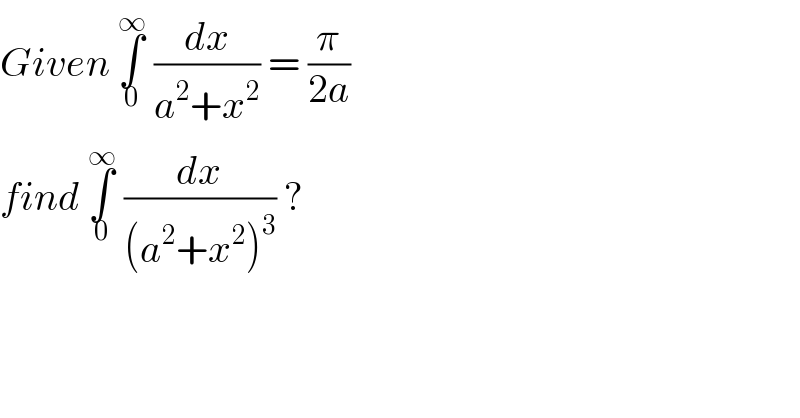
Commented by bemath last updated on 16/Jun/20
![(d/da) [∫_0 ^∞ (dx/(a^2 +x^2 )) ] = (d/da) [(π/(2a)) ] −2a ∫_0 ^∞ (dx/((a^2 +x^2 )^2 )) = ((−π)/(2a^2 )) ∫_0 ^∞ (dx/((a^2 +x^2 )^2 )) = (π/(4a^3 )) (d/da) [ ∫_0 ^∞ (dx/((a^2 +x^2 )^2 )) ] = (d/da) [(π/(4a^3 )) ] −4a ∫_0 ^∞ (dx/((a^2 +x^2 )^3 )) = ((−3π)/(4a^4 )) ∴ ∫_0 ^∞ (dx/((a^2 +x^2 )^3 )) = ((3π)/(16a^5 )) ■](Q98829.png)
Commented by bramlex last updated on 16/Jun/20

| ||
Question and Answers Forum | ||
Question Number 98826 by bramlex last updated on 16/Jun/20 | ||
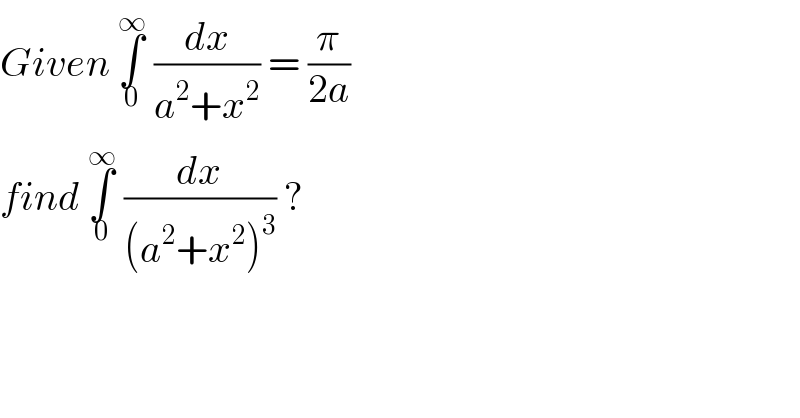 | ||
Commented by bemath last updated on 16/Jun/20 | ||
![(d/da) [∫_0 ^∞ (dx/(a^2 +x^2 )) ] = (d/da) [(π/(2a)) ] −2a ∫_0 ^∞ (dx/((a^2 +x^2 )^2 )) = ((−π)/(2a^2 )) ∫_0 ^∞ (dx/((a^2 +x^2 )^2 )) = (π/(4a^3 )) (d/da) [ ∫_0 ^∞ (dx/((a^2 +x^2 )^2 )) ] = (d/da) [(π/(4a^3 )) ] −4a ∫_0 ^∞ (dx/((a^2 +x^2 )^3 )) = ((−3π)/(4a^4 )) ∴ ∫_0 ^∞ (dx/((a^2 +x^2 )^3 )) = ((3π)/(16a^5 )) ■](Q98829.png) | ||
Commented by bramlex last updated on 16/Jun/20 | ||
 | ||