Question Number 98842 by M±th+et+s last updated on 16/Jun/20
$${let}\:{f}\left({x}\right)\:{be}\:{a}\:{dolvnomial}\:{of}\:{degree}\:\mathrm{4}\: \\ $$$${such}\:{that}\:{f}\left(\mathrm{1}\right)=\mathrm{1}\:,\:{f}\left(\mathrm{2}\right)=\mathrm{2}\:,{f}\left(\mathrm{3}\right)=\mathrm{3},{f}\left(\mathrm{4}\right)=\mathrm{4} \\ $$$${then}\:{f}\left(\mathrm{6}\right)=? \\ $$
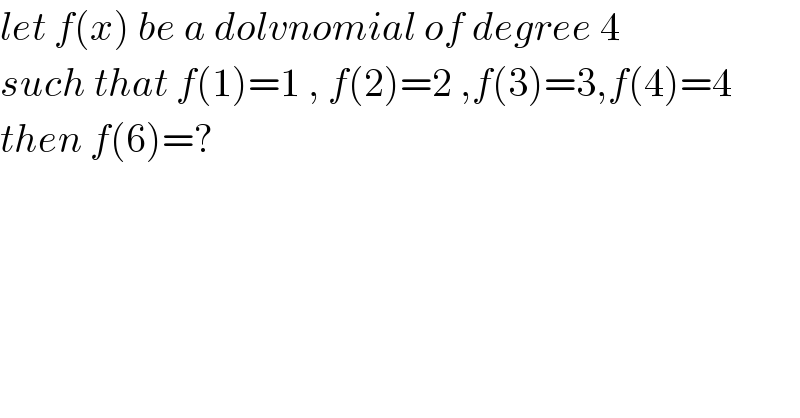
Commented by mr W last updated on 16/Jun/20
$${see}\:{also}\:{Q}\mathrm{98268} \\ $$
Answered by maths mind last updated on 16/Jun/20
![let p(x)=f(x)−x⇒P(x)∈R_4 [X] ⇒p(1)=p(2)=p(3)=p(4)=0 1,2,3,4 are roots of p p(x)=a(x−1)(x−2)(x−3)(x−4) f(x)=a(x−1)(x−2)(x−3)(x−4)+x f(6)=6+120a](Q98846.png)
$${let}\:{p}\left({x}\right)={f}\left({x}\right)−{x}\Rightarrow{P}\left({x}\right)\in\mathbb{R}_{\mathrm{4}} \left[{X}\right] \\ $$$$\Rightarrow{p}\left(\mathrm{1}\right)={p}\left(\mathrm{2}\right)={p}\left(\mathrm{3}\right)={p}\left(\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\:{are}\:{roots}\:{of}\:{p} \\ $$$${p}\left({x}\right)={a}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right) \\ $$$${f}\left({x}\right)={a}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)+{x} \\ $$$${f}\left(\mathrm{6}\right)=\mathrm{6}+\mathrm{120}{a} \\ $$
Commented by M±th+et+s last updated on 16/Jun/20
$${thank}\:{you}\:{sir} \\ $$
Answered by Rio Michael last updated on 17/Jun/20
$$\mathrm{Following}\:\mathrm{the}\:\mathrm{above}\:\mathrm{procedure}, \\ $$$$\mathrm{let}\:{p}\left({x}\right)\:=\:{f}\left({x}\right)−{x} \\ $$$$\Rightarrow\:{p}\left(\mathrm{1}\right)\:=\:{f}\left(\mathrm{1}\right)−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:{p}\left(\mathrm{2}\right)=\:{f}\left(\mathrm{2}\right)−\mathrm{2}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:{p}\left(\mathrm{3}\right)\:=\:{f}\left(\mathrm{3}\right)−\mathrm{3}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:{p}\left(\mathrm{4}\right)\:=\:{f}\left(\mathrm{4}\right)−\mathrm{4}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{f}\left({x}\right)\:=\:{p}\left({x}\right)+\:{x}\:\mathrm{where}\:{p}\left({x}\right)\:=\:\left({x}\:−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right) \\ $$$$\Rightarrow\:{f}\left({x}\right)\:=\:\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\:+\:{x}\:\: \\ $$$${f}\left(\mathrm{6}\right)\:=\:\left(\mathrm{5}\right)\left(\mathrm{4}\right)\left(\mathrm{3}\right)\left(\mathrm{2}\right)\:+\:\mathrm{6}\:=\:\mathrm{126} \\ $$
Commented by mr W last updated on 17/Jun/20
$$\mathrm{4}\:{conditions}\:{are}\:{not}\:{enough}\:{to} \\ $$$${uinquely}\:{define}\:{a}\:\mathrm{4}{th}\:{degree} \\ $$$${polynomial},\:{therefore}\:{there}\:{is}\:{no} \\ $$$${unique}\:{solution}\:{for}\:{f}\left({x}\right).\:{we}\:{can}\:{only} \\ $$$${say} \\ $$$${f}\left({x}\right)={k}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)+{x} \\ $$$${with}\:{k}={constant}\neq\mathrm{0} \\ $$$${f}\left(\mathrm{6}\right)=\mathrm{120}{k}+\mathrm{6} \\ $$
Commented by Rio Michael last updated on 17/Jun/20
$$\mathrm{thanks}\:\mathrm{sir},\mathrm{i}\:\mathrm{got}\:\mathrm{it}\:\mathrm{now}... \\ $$$$ \\ $$