Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 98859 by peter frank last updated on 16/Jun/20

Commented by mr W last updated on 16/Jun/20

$p (x) = q (x) (x - 1)$ $p (1) = 0$ $1 + c - 2 c + 4 = 0$ $\Rightarrow c = 5$
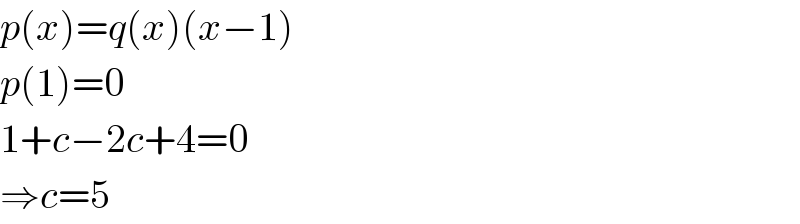
	Answered by Rasheed.Sindhi last updated on 16/Jun/20

	$(\begin{matrix} 1) & 1 & c & - 2 c & 4 \\ 1 & c + 1 & - c + 1 \\ 1 & c + 1 & - c + 1 & - c + 5 \end{matrix})$ $- c + 5 = 0 \Rightarrow c = 5$
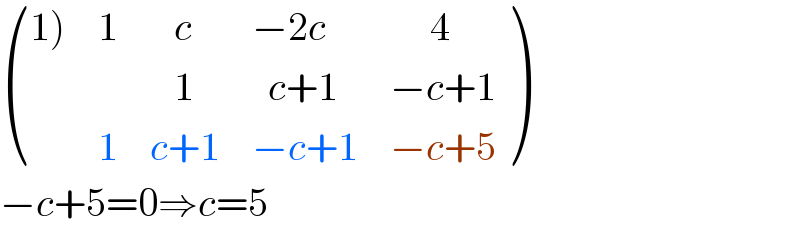
	Commented by Rio Michael last updated on 17/Jun/20

	$please i will love to study this method of$ $yours . . please hint me on how to use it .$
	Commented by Rasheed.Sindhi last updated on 17/Jun/20

	$L e t a p o l y n o m i a l P (x) i s d i v i d e d$ $b y x - r (S y n t h e t i c a l l y) .$ $1 . W r i t e P (x) i n d e s c e n d i n g o r d e r$ $i n c l u d i n g m i s s i n g t e r m s w i t h$ $c o e f f i c i e n t s 0 . F o r e x a m p l e$ $i f P (x) = 3 x^{2} - 8 + 4 x^{3}$ $t h e n P (x) = 4 x^{3} + 3 x^{2} + 0 x - 8$ $2 . T h e d i v i s o r s h o u l d b e o f t y p e$ $x - r . r i s c a l l e d m u l t i p l y e r$ $I n x - 3, t h e m u l t i p l y e r 3 a n d$ $i n x + 3 = x - (- 3) t h e m u l t i p l y e r$ $i s - 3 .$ $3 . F i r s t r o w c o n s i s t o f$ $m u l t i p l y e r, s e p a r a t o r & c o e f f i c i e n t s o f p (x)$ $P r o c e s s$ $E x a m p l e .$ $(C_{0} x^{3} + C_{1} x^{2} + C_{2} x + C_{3}) \div (x - r)$ $(1), . . ., (7) a r e e n t r i e s p r o c e s s e d i n o r d e r .$ $(\begin{matrix} r) & C_{0} & C_{1} & C_{2} & C_{3} \\ (2) & (4) & (6) \\ (1) & (3) & (5) & (7) \end{matrix})$ $(1) = C_{0}$ $(2) = (1) . r = C_{0} . r$ $(3) = C_{1} + (2)$ $(4) = (3) . r$ $(5) = C_{2} + (4)$ $(6) = (5) . r$ $(7) = C_{3} + (6) = r e m a i n d e r$ $(1) x^{2} + (3) x + (5) = q u o t i e n t$
	Commented by Rio Michael last updated on 17/Jun/20

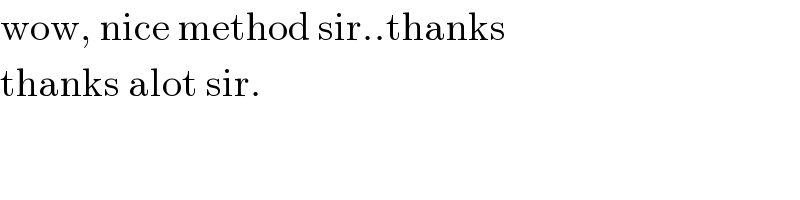
	$wow, nice method sir . . thanks$ $thanks alot sir .$
	Commented by bemath last updated on 18/Jun/20

	$Horner method sir$
	Answered by mathmax by abdo last updated on 16/Jun/20
	$p(x) =x^3 −1 +cx^2 −c −2c(x−1)−2c +4 +1+c =(x−1)(x^2 +x+1)+c(x−1)(x+1) −2c(x−1) +5−c =(x−1){x^2 +x+1 +cx−c) +5−c x−1 divide p(x) ⇒5−c =0 ⇒c=5 and p(x)=(x−1)Q(x) with Q(x)=x^2 +6x−4$
	$p (x) = x^{3} - 1 + {cx}^{2} - c - 2 c (x - 1) - 2 c + 4 + 1 + c$ $= (x - 1) (x^{2} + x + 1) + c (x - 1) (x + 1) - 2 c (x - 1) + 5 - c$ $= (x - 1) {x^{2} + x + 1 + cx - c) + 5 - c$ $x - 1 divide p (x) \Rightarrow 5 - c = 0 \Rightarrow c = 5 and p (x) = (x - 1) Q (x) with$ $Q (x) = x^{2} + 6 x - 4$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum