
Question and Answers Forum
Question Number 98952 by Ar Brandon last updated on 17/Jun/20
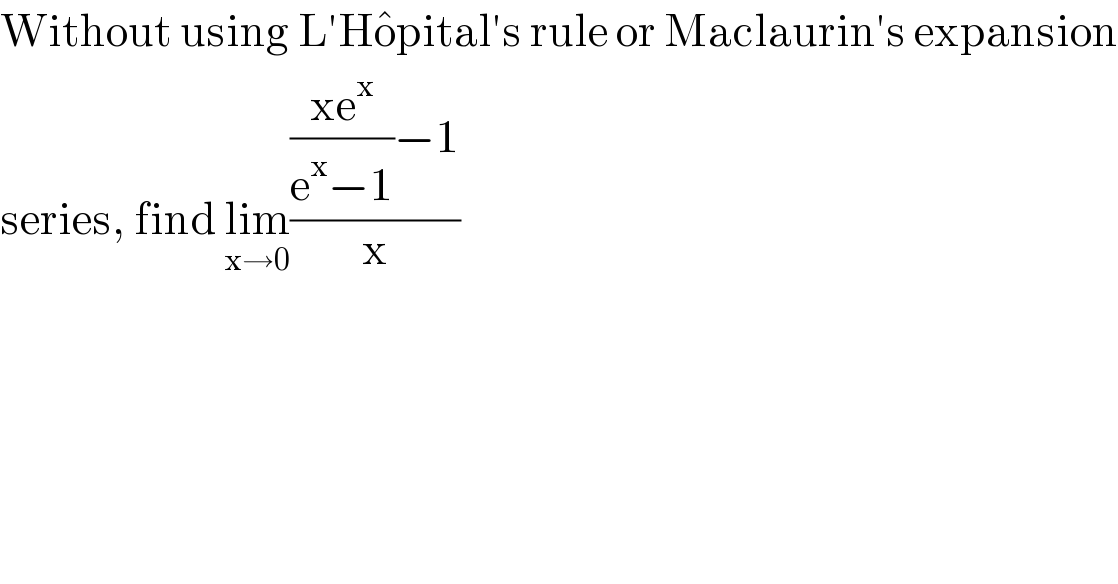
Commented by 675480065 last updated on 17/Jun/20
![let f(x)=((xe^x )/(e^x −1))−1 and g(x)=x from taylor series expansion e^x =1+x+(x^2 /2)+0(x^2 )⇒xe^x =x+x^2 +(x^3 /2)+0(x^3 ) e^x −1=1+x+(x^2 /2)+0(x^2 )−1=x+(x^2 /2)+0(x^2 ) ⇒f(x)=[((x(1+x+(x^2 /2)+0(x^2 )))/(x(1+(x/2)+0(x))))]−1 ⇒f(x)=[((1+x+(x^2 /2)−1−(x/2)+0(x^2 ))/((1+(x/2)+0(x))))]=[((x+x^2 +0(x^2 ))/((2+x+0(x))))] lim_(x→0) (((f(x))/(g(x))))=lim_(x→0) [((1+x+0(x))/(2+x+0(x)))]=(1/2)](Q98960.png)
| ||
Question and Answers Forum | ||
Question Number 98952 by Ar Brandon last updated on 17/Jun/20 | ||
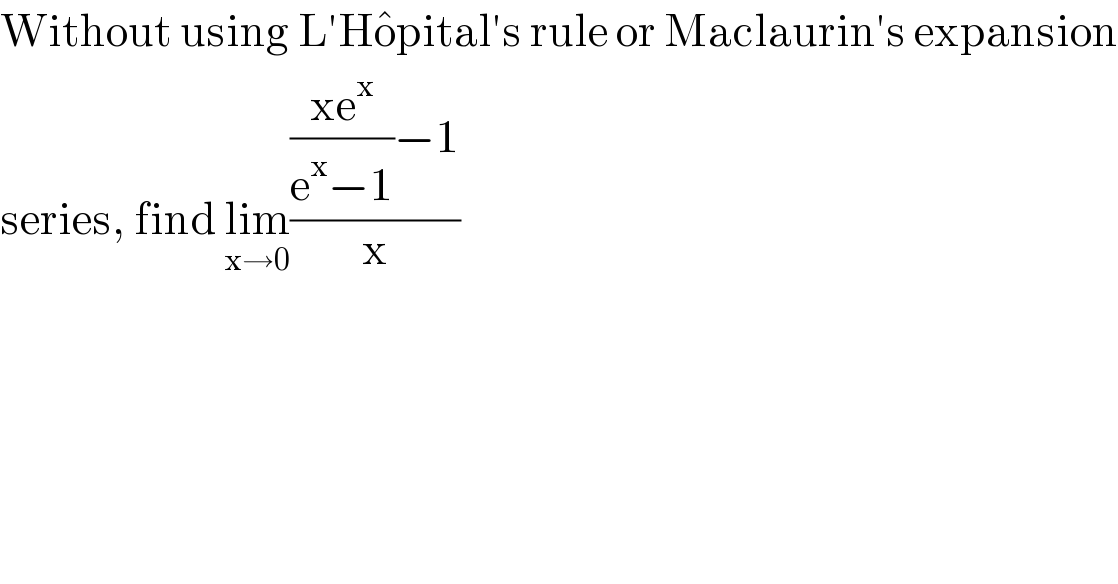 | ||
Commented by 675480065 last updated on 17/Jun/20 | ||
![let f(x)=((xe^x )/(e^x −1))−1 and g(x)=x from taylor series expansion e^x =1+x+(x^2 /2)+0(x^2 )⇒xe^x =x+x^2 +(x^3 /2)+0(x^3 ) e^x −1=1+x+(x^2 /2)+0(x^2 )−1=x+(x^2 /2)+0(x^2 ) ⇒f(x)=[((x(1+x+(x^2 /2)+0(x^2 )))/(x(1+(x/2)+0(x))))]−1 ⇒f(x)=[((1+x+(x^2 /2)−1−(x/2)+0(x^2 ))/((1+(x/2)+0(x))))]=[((x+x^2 +0(x^2 ))/((2+x+0(x))))] lim_(x→0) (((f(x))/(g(x))))=lim_(x→0) [((1+x+0(x))/(2+x+0(x)))]=(1/2)](Q98960.png) | ||