Previous in Differential Equation Next in Differential Equation
Question Number 98993 by Rio Michael last updated on 17/Jun/20
$$\mathrm{Use}\:\mathrm{the}\:\mathrm{laplace}\:\mathrm{tranform}\:\mathrm{to}\:\mathrm{solve}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\mathrm{5}\frac{{dy}}{{dx}}\:+\:\mathrm{6}{y}\:=\:{e}^{−{x}} \\ $$$$\mathrm{for}\:\:{y}\:=\:\mathrm{0},\:\mathrm{and}\:\frac{{dy}}{{dx}}\:=\:\mathrm{1}\:\mathrm{when}\:{x}\:=\:\mathrm{0} \\ $$
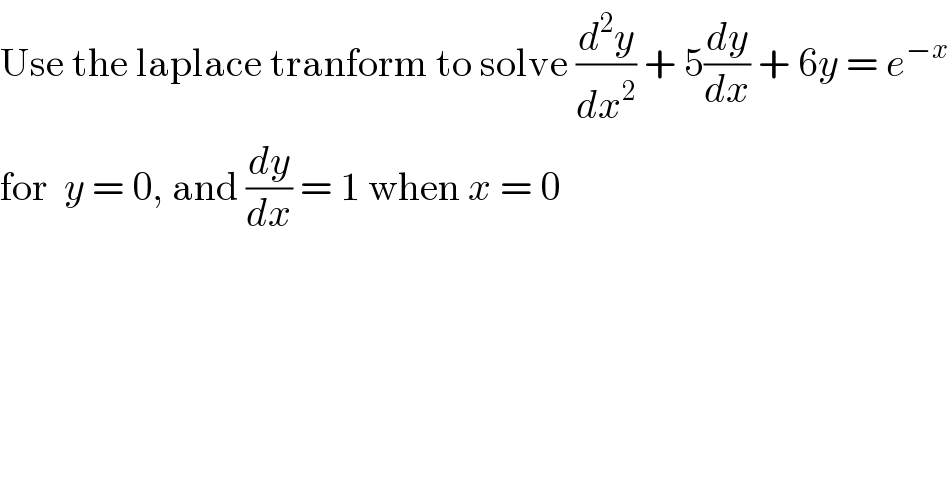
Answered by mathmax by abdo last updated on 18/Jun/20
![y^(′′) +5y^′ +6y =e^(−x) with y(0)=0 and y^′ (0) =1 (e) ⇒L(y^(′′) )+5L(y^′ )+6L(y) =L(e^(−x) ) ⇒ x^2 L(y)−x y(0)−y^′ (0) +5(x L(y)−y(0))+6L(y) =L(e^(−x) ) ⇒ (x^2 +5x +6)L(y) −1 = L(e^(−x) ) we have L(e^(−x) ) =∫_0 ^∞ e^(−t) e^(−xt) dt =∫_0 ^∞ e^(−(x+1)t) dt =[−(1/(x+1))e^(−(x+1)t) ]_0 ^∞ =(1/(x+1)) (e)⇒(x^2 +5x+6)L(y) =1+(1/(x+1)) =((x+2)/(x+1)) ⇒L(y) =((x+2)/((x+1)(x^2 +5x+6))) ⇒ y =L^(−1) (((x+2)/((x+1)(x^2 +5x +6)))) let decompose f(x) =((x+2)/((x+1)(x^2 +5x+6))) x^2 +5x +6 =0 →Δ =25−24 =1 ⇒x_1 =((−5+1)/2) =−2 and x_2 =((−5−1)/2) =−3 ⇒ f(x) =((x+2)/((x+1)(x+2)(x+3))) =(1/((x+1)(x+3))) =(1/2)((1/(x+1))−(1/(x+3))) ⇒ y(x)=L^(−1) (f) =(1/2)L^(−1) ((1/(x+1)))−(1/2)L^(−1) ((1/(x+3))) =(1/2)e^(−x) −(1/2)e^(−3x) the solution is y(x) =((e^(−x) −e^(−3x) )/2)](Q98997.png)
$$\mathrm{y}^{''} \:+\mathrm{5y}^{'} \:+\mathrm{6y}\:=\mathrm{e}^{−\mathrm{x}} \:\:\:\:\mathrm{with}\:\:\mathrm{y}\left(\mathrm{0}\right)=\mathrm{0}\:\mathrm{and}\:\mathrm{y}^{'} \left(\mathrm{0}\right)\:=\mathrm{1} \\ $$$$\left(\mathrm{e}\right)\:\Rightarrow\mathrm{L}\left(\mathrm{y}^{''} \right)+\mathrm{5L}\left(\mathrm{y}^{'} \right)+\mathrm{6L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{e}^{−\mathrm{x}} \right)\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{x}\:\mathrm{y}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)\:+\mathrm{5}\left(\mathrm{x}\:\mathrm{L}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{0}\right)\right)+\mathrm{6L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{e}^{−\mathrm{x}} \right)\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}\:+\mathrm{6}\right)\mathrm{L}\left(\mathrm{y}\right)\:−\mathrm{1}\:=\:\mathrm{L}\left(\mathrm{e}^{−\mathrm{x}} \right)\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{L}\left(\mathrm{e}^{−\mathrm{x}} \right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}} \\ $$$$\left(\mathrm{e}\right)\Rightarrow\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}+\mathrm{6}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:=\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}+\mathrm{1}}\:\Rightarrow\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}+\mathrm{6}\right)}\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5x}\:+\mathrm{6}\right)}\right)\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}+\mathrm{6}\right)} \\ $$$$\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}\:+\mathrm{6}\:=\mathrm{0}\:\rightarrow\Delta\:=\mathrm{25}−\mathrm{24}\:=\mathrm{1}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{5}+\mathrm{1}}{\mathrm{2}}\:=−\mathrm{2}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{5}−\mathrm{1}}{\mathrm{2}}\:=−\mathrm{3}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{3}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3}}\right)\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{L}^{−\mathrm{1}} \left(\mathrm{f}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}} \:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{3x}} \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{e}^{−\mathrm{x}} −\mathrm{e}^{−\mathrm{3x}} }{\mathrm{2}} \\ $$
Commented by Rio Michael last updated on 18/Jun/20
$$\mathrm{wow}\:\mathrm{nice}\:\mathrm{solution}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{i}\:\mathrm{have}\:\mathrm{problems}\:\mathrm{with} \\ $$$$\mathrm{L}\left({y}''\right)\:\mathrm{and}\:\mathrm{L}\left({y}''\right)\:\mathrm{the}\:\mathrm{derivations} \\ $$
Commented by abdomathmax last updated on 18/Jun/20
$$\mathrm{you}\:\mathrm{must}\:\mathrm{use}\:\mathrm{a}\:\mathrm{table}\:\mathrm{of}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{laplace} \\ $$