Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 99072 by Mr.D.N. last updated on 18/Jun/20

Answered by mr W last updated on 18/Jun/20

∫((x^2 +2x−1)/(2x^2 +3x+1))dx =(1/2)∫((2x^2 +4x−2)/(2x^2 +3x+1))dx =(1/2)∫((2x^2 +3x+1+x−3)/(2x^2 +3x+1))dx =(1/2)∫[1+(1/4)(((4x+3−15)/(2x^2 +3x+1)))]dx =(1/2)∫[1+(1/4)(((4x+3)/(2x^2 +3x+1)))−((15)/2)×(1/((2x+1)(2x+2)))]dx =(1/2){∫dx+(1/4)∫((d(2x^2 +3x+1))/(2x^2 +3x+1))−((15)/4)×∫((1/(2x+1))−(1/(2x+2)))d(2x)} =(1/2){x+(1/4)ln (2x^2 +3x+1)−((15)/4)ln ((2x+1)/(2(x+1)))}+C =(x/2)+(1/8)ln (2x+1)(x+1)−((15)/8)ln ((2x+1)/(x+1))+C =(x/2)−(7/4)ln (2x+1)+2 ln (x+1)+C

$$\int\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}+{x}−\mathrm{3}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{4}{x}+\mathrm{3}−\mathrm{15}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}\right)\right]{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{4}{x}+\mathrm{3}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}\right)−\frac{\mathrm{15}}{\mathrm{2}}×\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{2}\right)}\right]{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\int{dx}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{d}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}−\frac{\mathrm{15}}{\mathrm{4}}×\int\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}}\right){d}\left(\mathrm{2}{x}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{x}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)−\frac{\mathrm{15}}{\mathrm{4}}\mathrm{ln}\:\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{1}\right)}\right\}+{C} \\ $$$$=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\left(\mathrm{2}{x}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)−\frac{\mathrm{15}}{\mathrm{8}}\mathrm{ln}\:\frac{\mathrm{2}{x}+\mathrm{1}}{{x}+\mathrm{1}}+{C} \\ $$$$=\frac{{x}}{\mathrm{2}}−\frac{\mathrm{7}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}{x}+\mathrm{1}\right)+\mathrm{2}\:\mathrm{ln}\:\left({x}+\mathrm{1}\right)+{C} \\ $$

Commented by Mr.D.N. last updated on 18/Jun/20

awesome thank you mr. W keep rocking��������✍��

Commented by niroj last updated on 18/Jun/20

what grate deal.��

Answered by maths mind last updated on 18/Jun/20

cos(x)(y′′−2tg(x)y′−(a^2 +1)y=(1/(cos(x)))e^x )...E⇔ hello i think that sec=(1/(cos(x))) ....we not use it in french sorry my engilish is not good cos(x)y′′−2sin(x)y′−(a^2 +1)cos(x)y=e^x ...E let z=cos(x)y ⇒z′=cos(x)y′−sin(x)y z′′=−2sin(x)y′−cos(x)y+cos(x)y′′ z′′−a^2 z=e^x ,easy now try sir is mor helpfull for you than give all answer find Z than use y=(z/(cos(x))) i hop i help you verry nice day for all of you

$${cos}\left({x}\right)\left({y}''−\mathrm{2}{tg}\left({x}\right){y}'−\left({a}^{\mathrm{2}} +\mathrm{1}\right){y}=\frac{\mathrm{1}}{{cos}\left({x}\right)}{e}^{{x}} \right)...{E}\Leftrightarrow \\ $$$${hello}\:{i}\:{think}\:{that}\:\:{sec}=\frac{\mathrm{1}}{{cos}\left({x}\right)}\:\:....{we}\:{not}\:{use}\:{it}\:{in}\:{french}\: \\ $$$${sorry}\:{my}\:{engilish}\:{is}\:{not}\:{good}\: \\ $$$${cos}\left({x}\right){y}''−\mathrm{2}{sin}\left({x}\right){y}'−\left({a}^{\mathrm{2}} +\mathrm{1}\right){cos}\left({x}\right){y}={e}^{{x}} ...{E} \\ $$$${let}\:{z}={cos}\left({x}\right){y} \\ $$$$\Rightarrow{z}'={cos}\left({x}\right){y}'−{sin}\left({x}\right){y} \\ $$$${z}''=−\mathrm{2}{sin}\left({x}\right){y}'−{cos}\left({x}\right){y}+{cos}\left({x}\right){y}'' \\ $$$${z}''−{a}^{\mathrm{2}} {z}={e}^{{x}} \:\:\:\:,{easy}\:{now}\:{try}\:{sir}\:{is}\:{mor}\:{helpfull}\:{for}\:{you}\: \\ $$$${than}\:{give}\:{all}\:{answer} \\ $$$${find}\:{Z}\:{than}\:{use}\:{y}=\frac{{z}}{{cos}\left({x}\right)}\:\: \\ $$$${i}\:{hop}\:{i}\:{help}\:{you}\:{verry}\:{nice}\:{day}\:{for}\:{all}\:{of}\:{you} \\ $$$$ \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 18/Jun/20

let solve z^(′′) −a^2 z =e^x (he)→r^2 −a^2 =0 ⇒r =+^− a if a is real z_h =α e^(ax) +β e^(−ax) =αu_1 +βu_2 W(u_1 ,u_2 ) = determinant (((e^(ax) e^(−ax) )),((ae^(ax) −a e^(−ax) )))=−2a (we suppose a≠0) w_1 = determinant (((0 e^(−ax) )),((e^x −ae^(−ax) )))=−e^((1−a)x) W_2 = determinant (((e^(ax) 0)),((ae^x e^x )))=e^((a+1)x) v_1 =∫ (W_1 /W)dx =−∫ (e^((1−a)x) /(−2a)) dx =(1/(2a(1−a)))e^((1−a)x) v_2 =∫ (W_2 /W)dx =∫ (e^((a+1)x) /(−2a)) =−(1/(2a(a+1))) e^((a+1)x) Z_p =u_1 v_1 +u_2 v_2 =e^(ax) ×(1/(2a(1−a)))e^((1−a)x) −e^(−ax) ×(1/(2a(a+1)))e^((a+1)x) =(e^x /(2a(1−a))) −(e^x /(2a(1+a))) =(e^x /(2a))((1/(1−a))−(1/(1+a))) =(e^x /(2a))(((2a)/(1−a^2 ))) =(e^x /(1−a^2 )) the general solution is z =z_h +z_p =αe^(ax) +β e^(−ax) +(e^x /(1−a^2 )) (a^2 ≠1)

$$\mathrm{let}\:\mathrm{solve}\:\mathrm{z}^{''} −\mathrm{a}^{\mathrm{2}} \mathrm{z}\:=\mathrm{e}^{\mathrm{x}} \:\:\:\:\left(\mathrm{he}\right)\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow\mathrm{r}\:=\overset{−} {+}\mathrm{a}\:\:\mathrm{if}\:\mathrm{a}\:\mathrm{is}\:\mathrm{real}\: \\ $$$$\mathrm{z}_{\mathrm{h}} =\alpha\:\mathrm{e}^{\mathrm{ax}} \:+\beta\:\mathrm{e}^{−\mathrm{ax}} \:\:\:=\alpha\mathrm{u}_{\mathrm{1}} \:+\beta\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{ax}} \:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{ax}} }\\{\mathrm{ae}^{\mathrm{ax}} \:\:\:\:\:\:\:\:−\mathrm{a}\:\mathrm{e}^{−\mathrm{ax}} }\end{vmatrix}=−\mathrm{2a}\:\:\:\:\:\:\:\left(\mathrm{we}\:\mathrm{suppose}\:\mathrm{a}\neq\mathrm{0}\right) \\ $$$$\mathrm{w}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{ax}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:−\mathrm{ae}^{−\mathrm{ax}} }\end{vmatrix}=−\mathrm{e}^{\left(\mathrm{1}−\mathrm{a}\right)\mathrm{x}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{ax}} \:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{ae}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} }\end{vmatrix}=\mathrm{e}^{\left(\mathrm{a}+\mathrm{1}\right)\mathrm{x}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=−\int\:\:\frac{\mathrm{e}^{\left(\mathrm{1}−\mathrm{a}\right)\mathrm{x}} }{−\mathrm{2a}}\:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2a}\left(\mathrm{1}−\mathrm{a}\right)}\mathrm{e}^{\left(\mathrm{1}−\mathrm{a}\right)\mathrm{x}} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\frac{\mathrm{e}^{\left(\mathrm{a}+\mathrm{1}\right)\mathrm{x}} }{−\mathrm{2a}}\:=−\frac{\mathrm{1}}{\mathrm{2a}\left(\mathrm{a}+\mathrm{1}\right)}\:\mathrm{e}^{\left(\mathrm{a}+\mathrm{1}\right)\mathrm{x}} \\ $$$$\mathrm{Z}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =\mathrm{e}^{\mathrm{ax}} ×\frac{\mathrm{1}}{\mathrm{2a}\left(\mathrm{1}−\mathrm{a}\right)}\mathrm{e}^{\left(\mathrm{1}−\mathrm{a}\right)\mathrm{x}} \:−\mathrm{e}^{−\mathrm{ax}} \:×\frac{\mathrm{1}}{\mathrm{2a}\left(\mathrm{a}+\mathrm{1}\right)}\mathrm{e}^{\left(\mathrm{a}+\mathrm{1}\right)\mathrm{x}} \\ $$$$=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{2a}\left(\mathrm{1}−\mathrm{a}\right)}\:−\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{2a}\left(\mathrm{1}+\mathrm{a}\right)}\:=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{2a}}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}}\right)\:=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{2a}}\left(\frac{\mathrm{2a}}{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }\right)\:=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}−\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{z}\:=\mathrm{z}_{\mathrm{h}} \:+\mathrm{z}_{\mathrm{p}} =\alpha\mathrm{e}^{\mathrm{ax}} \:+\beta\:\mathrm{e}^{−\mathrm{ax}} \:\:+\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }\:\:\:\left(\mathrm{a}^{\mathrm{2}} \:\neq\mathrm{1}\right) \\ $$

Commented by Mr.D.N. last updated on 18/Jun/20

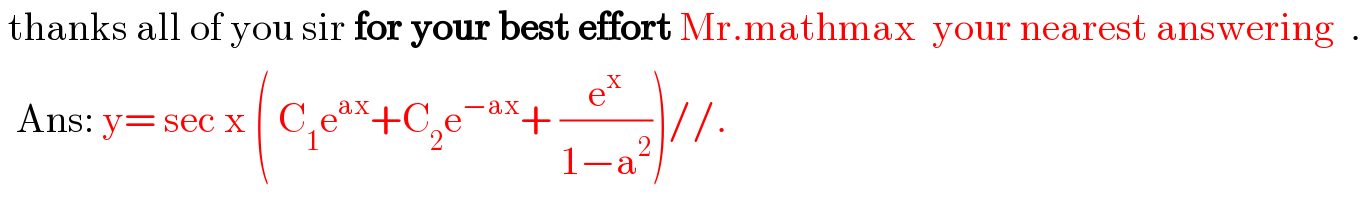
thanks all of you sir for your best effort Mr.mathmax your nearest answering . Ans: y= sec x ( C_1 e^(ax) +C_2 e^(−ax) + (e^x /(1−a^2 )))//.

$$\:\mathrm{thanks}\:\mathrm{all}\:\mathrm{of}\:\mathrm{you}\:\mathrm{sir}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{best}}\:\boldsymbol{\mathrm{effort}}\:\mathrm{Mr}.\mathrm{mathmax}\:\:\mathrm{your}\:\mathrm{nearest}\:\mathrm{answering}\:\:. \\ $$$$\:\:\mathrm{Ans}:\:\mathrm{y}=\:\mathrm{sec}\:\mathrm{x}\:\left(\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{ax}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{−\mathrm{ax}} +\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }\right)//. \\ $$

Commented by mathmax by abdo last updated on 18/Jun/20

you are welcome sir.

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com