Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 99077 by Mr.D.N. last updated on 18/Jun/20

Commented by MJS last updated on 18/Jun/20

$$\mathrm{the}\mathrm{colour}\mathrm{is}\mathrm{nice}\mathrm{but}\mathrm{hard}\mathrm{to}\mathrm{read}...$$

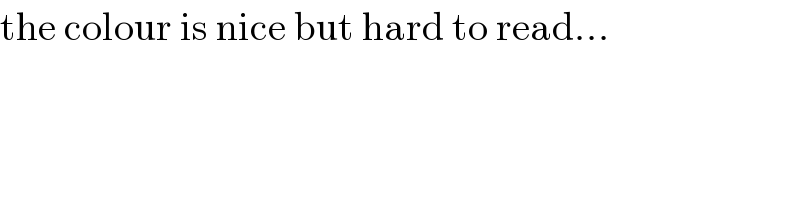
Commented by Rasheed.Sindhi last updated on 18/Jun/20

$$\mathcal{T}hen{it}^{\prime }snotnicehere!Main$$$$purposeistoberead.{Isn}^{\prime }tit?:)$$

Answered by mathmax by abdo last updated on 18/Jun/20

$$\mathrm{b})\mathrm{I}=\int \frac{{\mathrm{x}}^2+\mathrm{x}+1}{\sqrt{1-{\mathrm{x}}^2}}\mathrm{dx}\mathrm{changement}\mathrm{x}=\mathrm{sint}\mathrm{give}$$$$\mathrm{I}=\int \frac{{\sin }^2\mathrm{t}+\mathrm{sint}+1}{\mathrm{cost}}\mathrm{cost}\mathrm{dt}=\int ({\sin }^2\mathrm{t}+\mathrm{sint}+1)\mathrm{dt}$$$$=\int \frac{1-\cos \left(2\mathrm{t}\right)}{2}\mathrm{dt}-\mathrm{cost}+\mathrm{t}$$$$=\frac{\mathrm{t}}{2}-\frac{1}{4}\sin \left(2\mathrm{t}\right)-\mathrm{cost}+\mathrm{t}+\mathrm{c}$$$$=\frac{3}{2}\mathrm{t}-\frac{1}{2}\mathrm{sint}\mathrm{cost}-\mathrm{cost}+\mathrm{c}=\frac{3}{2}\mathrm{arcsinx}-\frac{\mathrm{x}}{2}\sqrt{1-{\mathrm{x}}^2}-\sqrt{1-{\mathrm{x}}^2}+\mathrm{c}$$

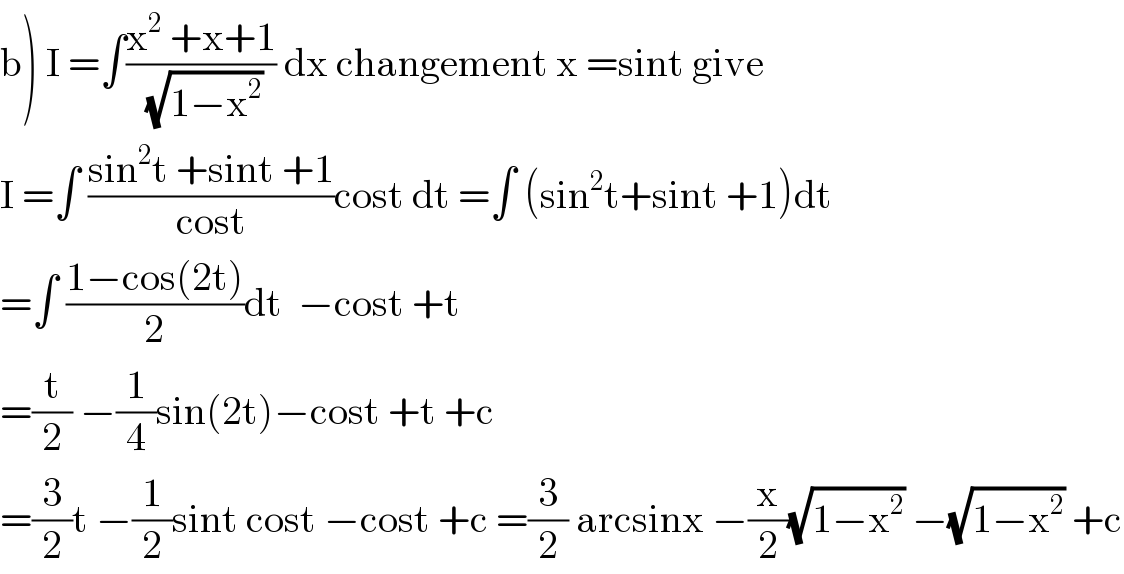
Commented by Mr.D.N. last updated on 18/Jun/20

thanks to your pleasure time.✍��

Commented by mathmax by abdo last updated on 18/Jun/20

$$\mathrm{you}\mathrm{are}\mathrm{welcome}.$$

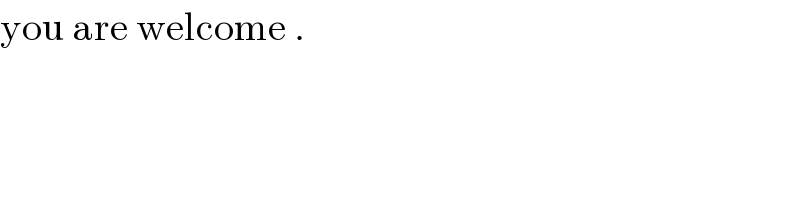
Answered by mathmax by abdo last updated on 18/Jun/20

$$\mathrm{a})\mathrm{at}\mathrm{form}\mathrm{of}\mathrm{serie}\mathrm{I}=\int \frac{{\mathrm{xe}}^{\mathrm{x}}}{{(\mathrm{x}+1)}^2}\mathrm{dx}\mathrm{changement}\mathrm{x}+1=\mathrm{t}\mathrm{give}$$$$\mathrm{I}=\int \frac{(\mathrm{t}-1){\mathrm{e}}^{\mathrm{t}-1}}{{\mathrm{t}}^2}\mathrm{dt}=\frac{1}{\mathrm{e}}\int \frac{(\mathrm{t}-1)}{{\mathrm{t}}^2}{\mathrm{e}}^{\mathrm{t}}\mathrm{dt}$$$$=\frac{1}{\mathrm{e}}\int (\frac{1}{\mathrm{t}}-\frac{1}{{\mathrm{t}}^2})\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{{\mathrm{t}}^{\mathrm{n}}}{\mathrm{n}!}\mathrm{dt}=\frac{1}{\mathrm{e}}\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{1}{\mathrm{n}!}\int ({\mathrm{t}}^{\mathrm{n}-1}-{\mathrm{t}}^{\mathrm{n}-2})\mathrm{dt}$$$$=\frac{1}{\mathrm{e}}\sum _{\mathrm{n}=2}^{\mathrm{\infty }}\frac{1}{\mathrm{n}!}(\frac{{\mathrm{t}}^{\mathrm{n}}}{\mathrm{n}}-\frac{{\mathrm{t}}^{\mathrm{n}-1}}{\mathrm{n}-1})+\frac{1}{\mathrm{e}}\int (\frac{1}{\mathrm{t}}-\frac{1}{{\mathrm{t}}^2})\mathrm{dt}+\frac{1}{\mathrm{e}}\int (1-\frac{1}{\mathrm{t}})\mathrm{dt}$$$$=\frac{1}{\mathrm{e}}\sum _{\mathrm{n}=2}^{\mathrm{\infty }}\frac{{\mathrm{t}}^{\mathrm{n}}}{\mathrm{n}(\mathrm{n}!)}-\frac{1}{\mathrm{e}}\sum _{\mathrm{n}=2}^{\mathrm{\infty }}\frac{{\mathrm{t}}^{\mathrm{n}-1}}{(\mathrm{n}-1)\mathrm{n}!}+\frac{\ln \mid \mathrm{t}\mid }{\mathrm{e}}+\frac{1}{\mathrm{et}}+\frac{\mathrm{t}}{\mathrm{e}}-\frac{\ln \mid \mathrm{t}\mid }{\mathrm{e}}$$$$=\frac{1}{\mathrm{e}}\sum _{\mathrm{n}=2}^{\mathrm{\infty }}\frac{{(\mathrm{x}+1)}^{\mathrm{n}}}{\mathrm{n}(\mathrm{n}!)}-\frac{1}{\mathrm{e}}\sum _{\mathrm{n}=2}^{\mathrm{\infty }}\frac{{(\mathrm{x}+1)}^{\mathrm{n}-1}}{(\mathrm{n}-1)\mathrm{n}!}+\frac{1}{\mathrm{e}(\mathrm{x}+1)}+\frac{\mathrm{x}+1}{\mathrm{e}}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com