solve y^(′′) +5y^′ −3y =x^2 sin(3x) with y(0) =0 and y^′ (0)=−1


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 99113 by mathmax by abdo last updated on 18/Jun/20

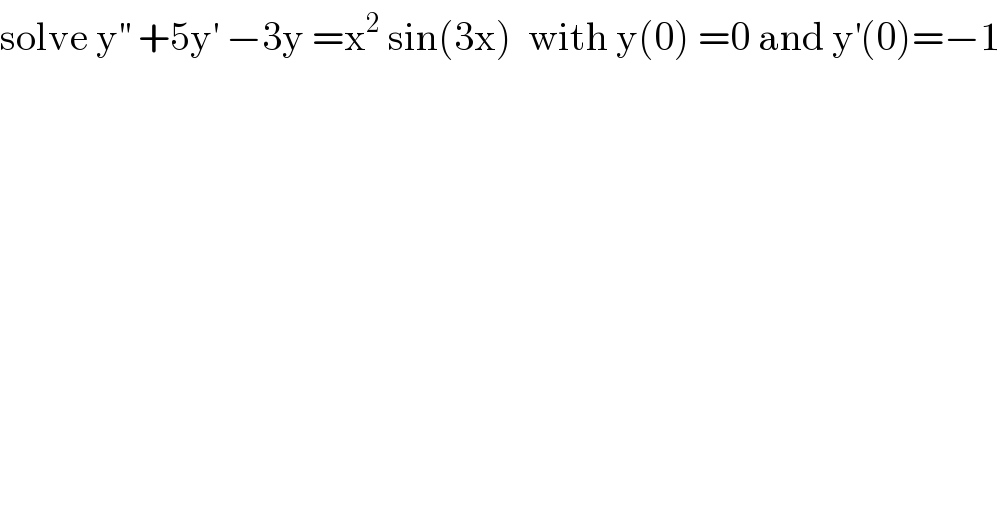
$solve y^{^{″}} + {5 y}^{^{'}} - 3 y = x^{2} \sin (3 x) with y (0) = 0 and y^{^{'}} (0) = - 1$
	Answered by mathmax by abdo last updated on 19/Jun/20

	$(he) \to y^{^{″}} + {5 y}^{^{'}} - 3 y = 0 \to r^{2} + 5 y - 3 = 0$ $Δ = 25 + 12 = 37 \Rightarrow r_{1} = \frac{- 5 + \sqrt{37}}{2} and r_{2} = \frac{- 5 - \sqrt{37}}{2} \Rightarrow y_{h} = α e^{r_{1} x} + β e^{r_{2} x}$ $= α u_{1} + β u_{2}$ $W (u_{1}, u_{2}) = \| \begin{matrix} e^{r_{1} x} e^{r_{2} x} \\ r_{1} e^{r_{1} x} r_{2} e^{r_{2} x} \end{matrix} \| = (r_{2} - r_{1}) e^{(r_{1} + r_{2}) x} = - \sqrt{37} e^{- 5 x}$ $W_{1} = \| \begin{matrix} 0 e^{r_{2} x} \\ x^{2} \sin (3 x) r_{2} e^{r_{2} x} \end{matrix} \| = - x^{2} \sin (3 x) e^{r_{2} x}$ $W_{2} = \| \begin{matrix} e^{r_{1} x} 0 \\ r_{1} e^{r_{1} x} x^{2} \sin (3 x) \end{matrix} \| = x^{2} \sin (3 x) e^{r_{1} x}$ $v_{1} = \int \frac{W 1}{W} dx = \int \frac{- x^{2} \sin (3 x) e^{r_{2} x}}{- \sqrt{37} e^{- 5 x}} dx = \frac{1}{\sqrt{37}} \int x^{2} \sin (3 x) e^{(5 + r_{2}) x} dx$ $= \frac{1}{\sqrt{37}} Im (\int x^{2} e^{(3 i + 5 + r_{2}) x} dx) = . . . .$ $v_{2} = \int \frac{W_{2}}{W} dx = \int \frac{x^{2} \sin (3 x) e^{r_{1} x}}{- \sqrt{37} e^{- 5 x}} dx = - \frac{1}{\sqrt{37}} \int x^{2} \sin (3 x) e^{(5 + r_{1}) x} dx$ $= - \frac{1}{\sqrt{37}} Im (\int x^{2} e^{(3 i + 5 + r_{1}) x} dx) = . . . . \Rightarrow$ $y_{p} = u_{1} v_{1} + u_{2} v_{2} and general solution is y = α e^{r_{1} x} + β e^{r_{2} x} + y_{p}$
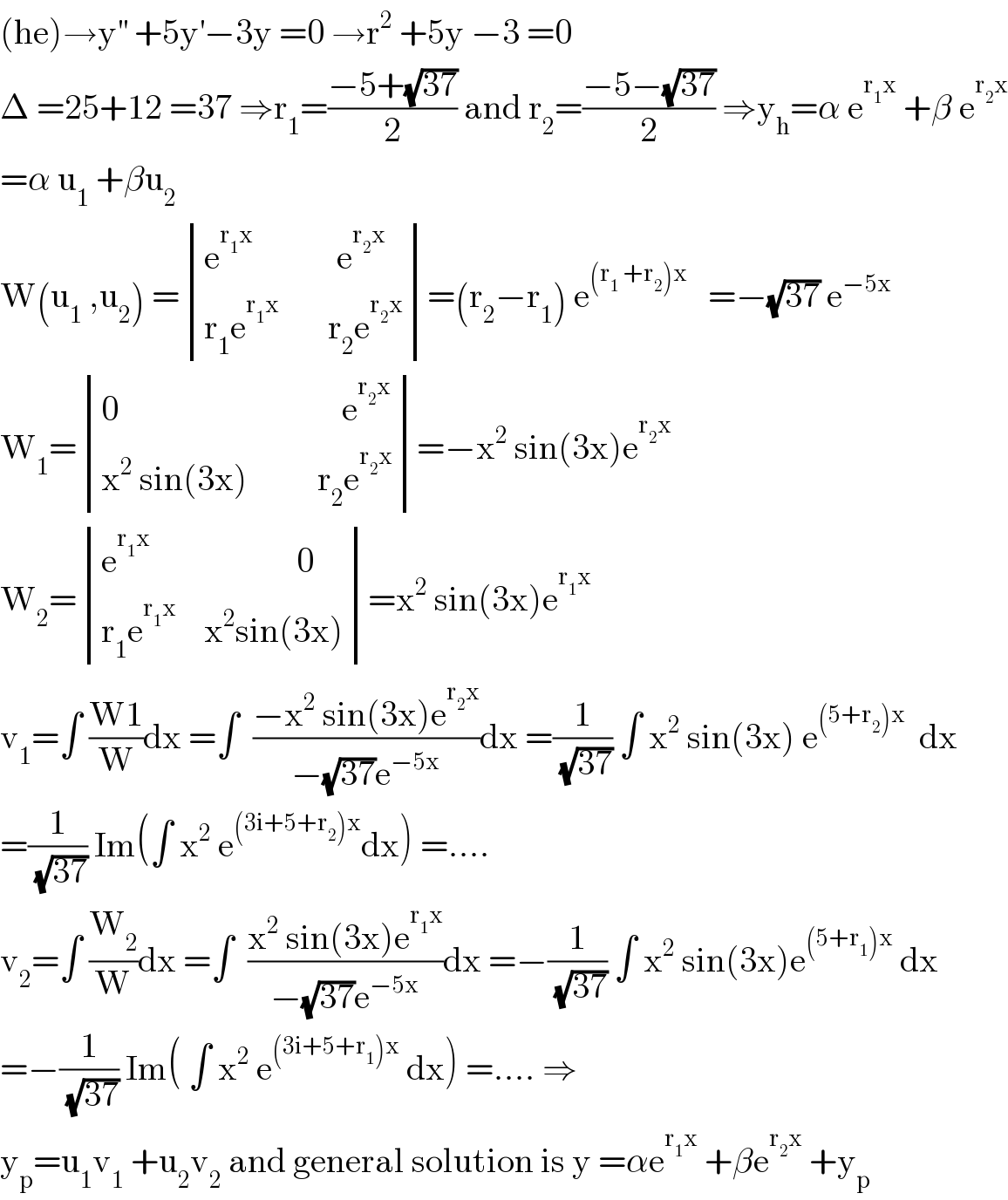
	Answered by mathmax by abdo last updated on 20/Jun/20
	$let take a try with laplace transform e ⇒L(y^(′′) )+5L(y^′ )−3L(y) =L(x^2 sin(3x)) ⇒ x^2 L(y)−xy(0)−y^′ (0)+5(x L(y)−y(0))−3L(y) =L(x^2 sin(3x)) ⇒ (x^2 +5x−3)L(y) +1 =L(x^2 sin(3x) we have L(x^2 sin(3x)) =∫_0 ^∞ t^2 sin(3t) e^(−xt) dt =Im(∫_0 ^∞ t^2 e^((3i−x)t) dt) ∫_0 ^∞ t^2 e^((−x+3i)t) dt =[(t^2 /(−x+3i)) e^((−x+3i)t) ]_0 ^(+∞) −∫_0 ^∞ ((2t)/(−x+3i)) e^((−x+3i)t) dt =(2/(x−3i)) ∫_0 ^∞ t e^((−x+3i)t) dt =(2/(x−3i)){ [(t/(−x+3i)) e^((−x+3i)t) ]_0 ^(+∞) −∫_0 ^∞ (1/(−x+3i)) e^((−x+3i)t) dt} =(2/(x−3i))×(1/(x−3i)) ∫_0 ^∞ e^((−x+3i)t) dt =(2/((x−3i)^2 ))×[(1/(−x+3i)) e^((−x+3i)t) ]_0 ^(+∞) =(2/((x−3i)^3 )) =((2(x+3i)^3 )/((x^2 +9)^3 )) =((2(x^3 +3x^2 (3i)+3x(3i)^2 +(3i)^3 ))/((x^2 +9)^3 )) =((2(x^3 +9ix^2 −27x −27i))/((x^2 +9)^3 )) ⇒Im(...) =((2(9x^2 −27))/((x^2 +9)^3 )) e ⇒(x^2 +5x−3)L(y) =−1 +((18x^3 −54)/((x^2 +9)^3 )) ⇒ L(y) =−(1/(x^2 +5x−3)) +((18x^3 −54)/((x^2 +5x−3)(x^2 +9)^3 )) ⇒ y(x) =−L^(−1) ((1/(x^2 +5x −3)))+L^(−1) (((18x^3 −54)/((x^2 +5x−3)(x^2 +9)^3 )))...be continued....$
	$let take a try with laplace transform$ $e \Rightarrow L (y^{^{″}}) + 5 L (y^{^{'}}) - 3 L (y) = L (x^{2} \sin (3 x)) \Rightarrow$ $x^{2} L (y) - xy (0) - y^{^{'}} (0) + 5 (x L (y) - y (0)) - 3 L (y) = L (x^{2} \sin (3 x)) \Rightarrow$ $(x^{2} + 5 x - 3) L (y) + 1 = L (x^{2} \sin (3 x) we have$ $L (x^{2} \sin (3 x)) = \int_{0}^{\infty} t^{2} \sin (3 t) e^{- xt} dt = Im (\int_{0}^{\infty} t^{2} e^{(3 i - x) t} dt)$ $\int_{0}^{\infty} t^{2} e^{(- x + 3 i) t} dt = {[\frac{t^{2}}{- x + 3 i} e^{(- x + 3 i) t}]}_{0}^{+ \infty} - \int_{0}^{\infty} \frac{2 t}{- x + 3 i} e^{(- x + 3 i) t} dt$ $= \frac{2}{x - 3 i} \int_{0}^{\infty} t e^{(- x + 3 i) t} dt = \frac{2}{x - 3 i} {{[\frac{t}{- x + 3 i} e^{(- x + 3 i) t}]}_{0}^{+ \infty} - \int_{0}^{\infty} \frac{1}{- x + 3 i} e^{(- x + 3 i) t} dt}$ $= \frac{2}{x - 3 i} \times \frac{1}{x - 3 i} \int_{0}^{\infty} e^{(- x + 3 i) t} dt = \frac{2}{{(x - 3 i)}^{2}} \times {[\frac{1}{- x + 3 i} e^{(- x + 3 i) t}]}_{0}^{+ \infty}$ $= \frac{2}{{(x - 3 i)}^{3}} = \frac{2 {(x + 3 i)}^{3}}{{(x^{2} + 9)}^{3}} = \frac{2 (x^{3} + {3 x}^{2} (3 i) + 3 x {(3 i)}^{2} + {(3 i)}^{3})}{{(x^{2} + 9)}^{3}}$ $= \frac{2 (x^{3} + {9 ix}^{2} - 27 x - 27 i)}{{(x^{2} + 9)}^{3}} \Rightarrow Im (. . .) = \frac{2 ({9 x}^{2} - 27)}{{(x^{2} + 9)}^{3}}$ $e \Rightarrow (x^{2} + 5 x - 3) L (y) = - 1 + \frac{{18 x}^{3} - 54}{{(x^{2} + 9)}^{3}} \Rightarrow$ $L (y) = - \frac{1}{x^{2} + 5 x - 3} + \frac{{18 x}^{3} - 54}{(x^{2} + 5 x - 3) {(x^{2} + 9)}^{3}} \Rightarrow$ $y (x) = - L^{- 1} (\frac{1}{x^{2} + 5 x - 3}) + L^{- 1} (\frac{{18 x}^{3} - 54}{(x^{2} + 5 x - 3) {(x^{2} + 9)}^{3}}) . . . be continued . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum