
Question and Answers Forum
Question Number 99120 by M±th+et+s last updated on 18/Jun/20
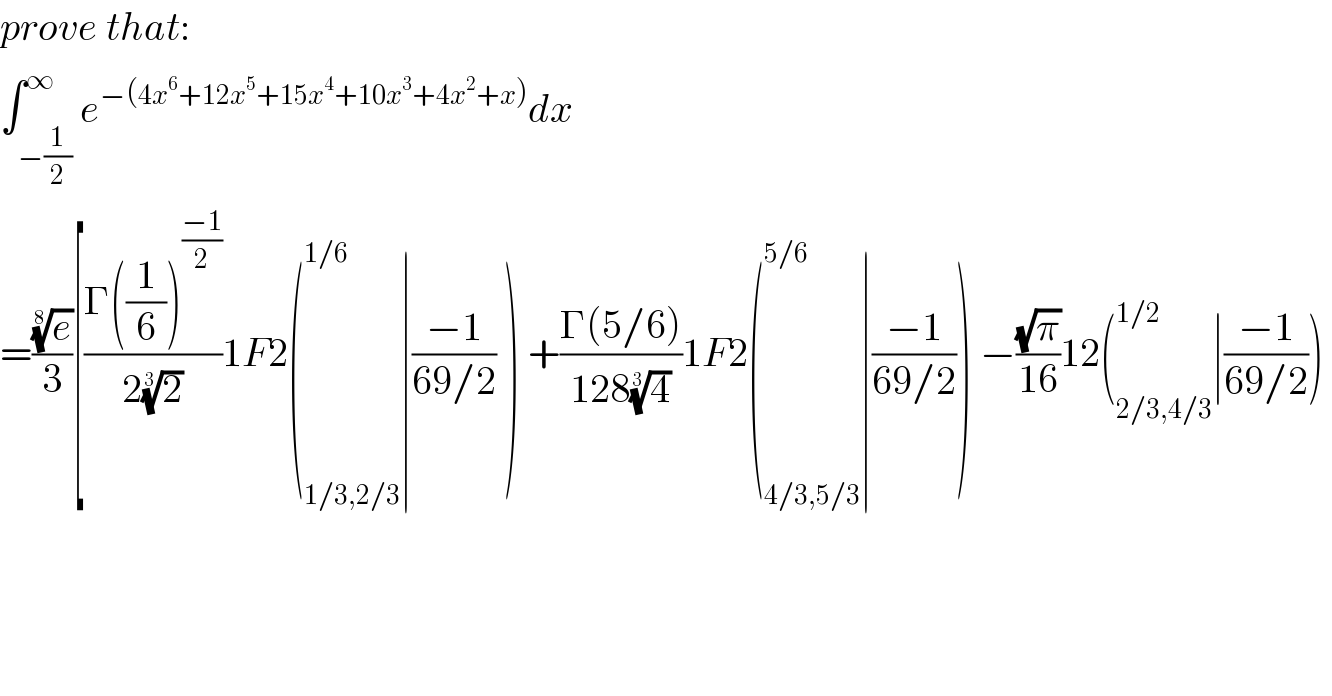
Commented by M±th+et+s last updated on 18/Jun/20
![I=(((e)^(1/8) .π(√π))/(2(4)^(1/3) (3)^(1/6) ))[(Ai(((−1)/(8(6)^(1/3) ))))^2 +(Bi(((−1)/(8(6)^(1/3) ))))^2 ]](Q99121.png)
Commented by M±th+et+s last updated on 18/Jun/20

| ||
Question and Answers Forum | ||
Question Number 99120 by M±th+et+s last updated on 18/Jun/20 | ||
 | ||
Commented by M±th+et+s last updated on 18/Jun/20 | ||
![I=(((e)^(1/8) .π(√π))/(2(4)^(1/3) (3)^(1/6) ))[(Ai(((−1)/(8(6)^(1/3) ))))^2 +(Bi(((−1)/(8(6)^(1/3) ))))^2 ]](Q99121.png) | ||
Commented by M±th+et+s last updated on 18/Jun/20 | ||
 | ||