
Question and Answers Forum
Question Number 99146 by mathmax by abdo last updated on 18/Jun/20
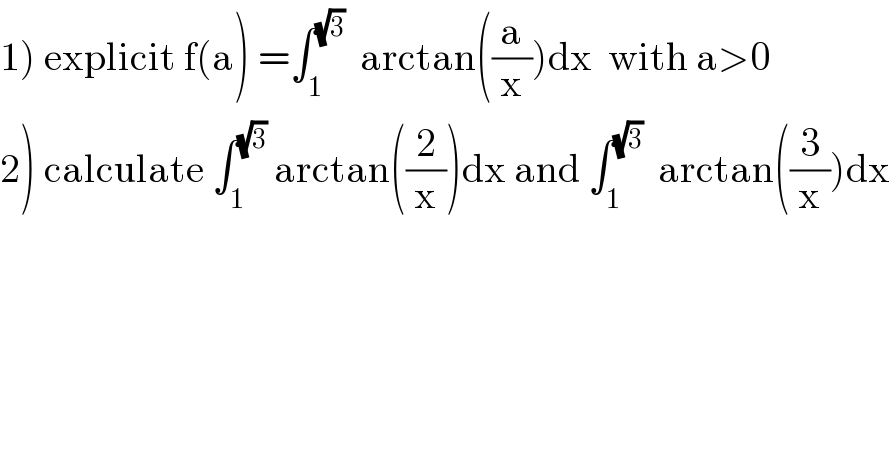
Answered by mathmax by abdo last updated on 19/Jun/20
![1) f(a) =∫_1 ^(√3) arctan((a/x))dx by parts we get f(a) =[xarctan((a/x))]_1 ^(√3) −∫_1 ^(√3) x(−(a/x^2 ))×(1/(1+(a^2 /x^2 ))) dx =(√3)arctan((a/(√3)))−arctan(a) +∫_1 ^(√3) ((ax)/(x^2 +a^2 )) dx but ∫_1 ^(√3) ((ax)/(x^2 +a^2 )) dx =_(x=au) ∫_(1/a) ^((√3)/a) ((a(au))/(a^2 (1+u^2 ))) adu =a ∫_(1/a) ^((√3)/a) ((udu)/(1+u^2 )) =(a/2)[ln(1+u^2 )]_(1/a) ^((√3)/a) =(a/2){ln(1+(3/a^2 ))−ln(1+(1/a^2 ))} =(a/2)ln(((a^2 +3)/(a^2 +1))) ⇒ f(a) =(√3)arctan((a/(√3)))−arctan(a)+(a/2)ln(((3+a^2 )/(1+a^2 ))) 2)∫_1 ^(√3) artan((2/x))dx =f(2) =(√3) arctan((2/(√3)))−arctan(2)+ln((7/5)) ∫_1 ^(√3) arctan((3/x))dx =f(3) =(√3) arctan((√3))−arctan(3)+(3/2)ln((6/5))](Q99216.png)
| ||
Question and Answers Forum | ||
Question Number 99146 by mathmax by abdo last updated on 18/Jun/20 | ||
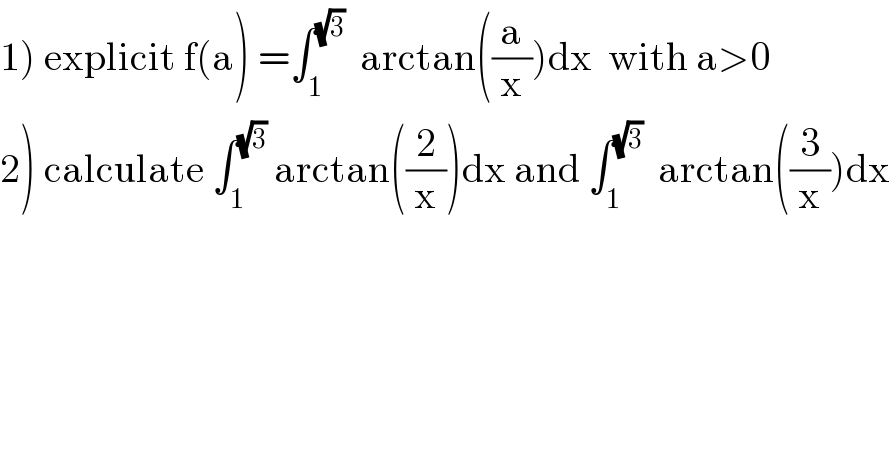 | ||
Answered by mathmax by abdo last updated on 19/Jun/20 | ||
![1) f(a) =∫_1 ^(√3) arctan((a/x))dx by parts we get f(a) =[xarctan((a/x))]_1 ^(√3) −∫_1 ^(√3) x(−(a/x^2 ))×(1/(1+(a^2 /x^2 ))) dx =(√3)arctan((a/(√3)))−arctan(a) +∫_1 ^(√3) ((ax)/(x^2 +a^2 )) dx but ∫_1 ^(√3) ((ax)/(x^2 +a^2 )) dx =_(x=au) ∫_(1/a) ^((√3)/a) ((a(au))/(a^2 (1+u^2 ))) adu =a ∫_(1/a) ^((√3)/a) ((udu)/(1+u^2 )) =(a/2)[ln(1+u^2 )]_(1/a) ^((√3)/a) =(a/2){ln(1+(3/a^2 ))−ln(1+(1/a^2 ))} =(a/2)ln(((a^2 +3)/(a^2 +1))) ⇒ f(a) =(√3)arctan((a/(√3)))−arctan(a)+(a/2)ln(((3+a^2 )/(1+a^2 ))) 2)∫_1 ^(√3) artan((2/x))dx =f(2) =(√3) arctan((2/(√3)))−arctan(2)+ln((7/5)) ∫_1 ^(√3) arctan((3/x))dx =f(3) =(√3) arctan((√3))−arctan(3)+(3/2)ln((6/5))](Q99216.png) | ||
| ||