
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 99236 by abdomathmax last updated on 19/Jun/20
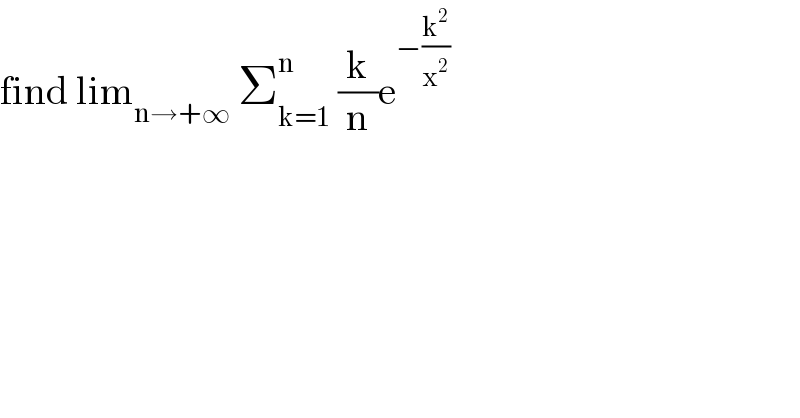
Commented by Ar Brandon last updated on 19/Jun/20
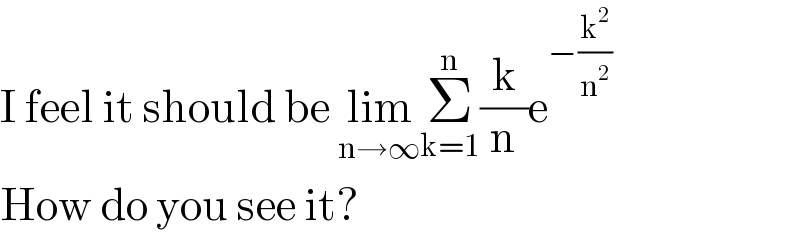
Answered by mathmax by abdo last updated on 21/Jun/20
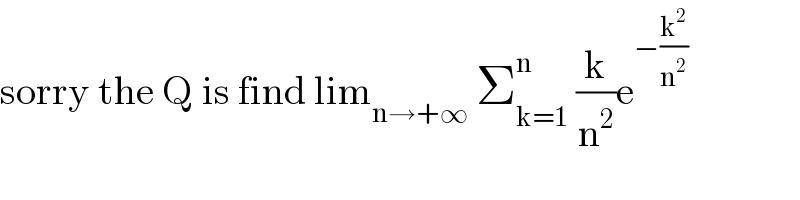
Answered by Ar Brandon last updated on 21/Jun/20
![l=lim_(n→∞) Σ_(k=1) ^n (k/n)e^(−(k^2 /n^2 )) =lim_(n→∞) n∙(1/n)Σ_(k=1) ^n (k/n)e^(−(k^2 /n^2 )) =lim_(n→∞) n∫_0 ^1 xe^(−x^2 ) dx=lim_(n→∞) −(n/2)∫_0 ^1 −2xe^(−x^2 ) dx =lim_(n→∞) −[(n/2)e^(−x^2 ) ]_0 ^1 =lim_(n→∞) {−(n/2)[(1/e)−1]}=+∞ {(1/e)−1<0}](Q99454.png)
