Previous in Relation and Functions Next in Relation and Functions
Question Number 99237 by abdomathmax last updated on 19/Jun/20
$$\mathrm{calculate}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\:\:\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\:\frac{\sqrt{\mathrm{kn}}}{\left(\mathrm{k}^{\mathrm{2}} \:+\mathrm{n}^{\mathrm{2}} \right)} \\ $$
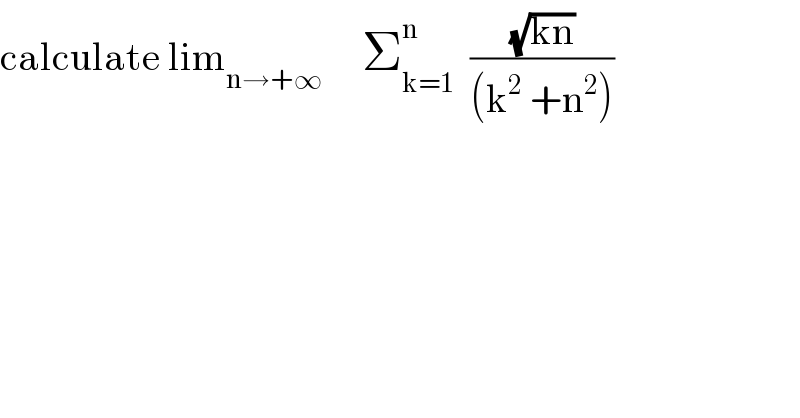
Answered by Ar Brandon last updated on 19/Jun/20
![l=lim_(n→∞) Σ_(k=1) ^n ((√(kn))/((k^2 +n^2 )))=lim_(n→∞) Σ_(k=1) ^n ((√((kn^2 )/n))/((k^2 +n^2 )))=lim_(n→∞) (n/n^2 )Σ_(n→∞) ^n ((√(k/n))/([(k^2 /n^2 )+1])) =∫_1 ^2 ((√x)/(x^2 +1))dx , t^2 =x⇒2tdt=dx ⇒l=∫_1 ^(√2) ((2t^2 )/(t^4 +1))dt=∫_1 ^(√2) (((t^2 +1)+(t^2 −1))/(t^4 +1))dt=∫_1 ^(√2) ((t^2 +1)/(t^4 +1))dt+∫_1 ^(√2) ((t^2 −1)/(t^4 +1))dt =∫_1 ^(√2) ((1+(1/t^2 ))/(t^2 +(1/t^2 )))dt+∫_1 ^(√2) ((1−(1/t^2 ))/(t^2 +(1/t^2 )))dt=∫_1 ^(√2) ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt+∫_1 ^(√2) ((1−(1/t^2 ))/((t+(1/t))^2 −2))dt u=t−(1/t)⇒du=(1+(1/t^2 ))dt, v=t+(1/t)⇒dv=(1−(1/t^2 ))dt ⇒l=∫_0 ^(1/(√2)) (du/(u^2 +2))+∫_2 ^(3/(√2)) (dv/(v^2 −2))=[(1/(√2))tan^(−1) ((u/(√2)))]_0 ^(1/(√2)) −[(1/(√2))tanh^(−1) ((v/(√2)))]_2 ^(3/(√2)) ⇒l=(1/(√2))[tan^(−1) ((1/2))]−(1/(√2))[tanh^(−1) ((3/2))−tanh^(−1) ((√2))] undefined { (),() :}f(x)=tanh^(−1) x⇒x∈]−1,1[](Q99252.png)
$${l}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\sqrt{\mathrm{kn}}}{\left(\mathrm{k}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right)}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\sqrt{\frac{\mathrm{kn}^{\mathrm{2}} }{\mathrm{n}}}}{\left(\mathrm{k}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right)}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} }\underset{\mathrm{n}\rightarrow\infty} {\overset{\mathrm{n}} {\sum}}\frac{\sqrt{\frac{\mathrm{k}}{\mathrm{n}}}}{\left[\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }+\mathrm{1}\right]} \\ $$$$\:\:=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\sqrt{\mathrm{x}}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:\:,\:\mathrm{t}^{\mathrm{2}} =\mathrm{x}\Rightarrow\mathrm{2tdt}=\mathrm{dx} \\ $$$$\Rightarrow{l}=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{2t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\mathrm{dt}=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)+\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\mathrm{dt}=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\mathrm{dt}+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\mathrm{dt} \\ $$$$\:\:\:\:\:\:=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} +\mathrm{2}}\mathrm{dt}+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} −\mathrm{2}}\mathrm{dt} \\ $$$$\mathrm{u}=\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\Rightarrow\mathrm{du}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt},\:\:\mathrm{v}=\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\Rightarrow\mathrm{dv}=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$\Rightarrow{l}=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{2}}+\int_{\mathrm{2}} ^{\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}} \frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}=\left[\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{u}}{\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} −\left[\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\mathrm{v}}{\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{2}} ^{\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}} \\ $$$$\Rightarrow{l}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right]−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left[\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{tanh}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}\right)\right] \\ $$$$\left.\mathrm{undefined\begin{cases}{}\\{}\end{cases}f}\left(\mathrm{x}\right)=\mathrm{tanh}^{−\mathrm{1}} \mathrm{x}\Rightarrow\mathrm{x}\in\right]−\mathrm{1},\mathrm{1}\left[\right. \\ $$
Commented by abdomathmax last updated on 19/Jun/20
$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
Commented by mathmax by abdo last updated on 21/Jun/20
$$\mathrm{oo}\:\mathrm{yes}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:... \\ $$
Commented by mathmax by abdo last updated on 21/Jun/20
![t+(1/t) =v ⇒ ∫_0 ^1 ((1−(1/t^2 ))/((t+(1/t))^2 −2))dt =−∫_2 ^∞ (dv/(v^2 −2)) =−(1/(2(√2)))∫_2 ^∞ ((1/(v−(√2)))−(1/(v+(√2))))dv =−(1/(2(√2)))[ln∣((v−(√2))/(v+(√2)))∣]_2 ^∞ =(1/(2(√2)))ln(((2−(√2))/(2+(√2)))) ⇒ I =(π/(2(√2))) +(1/(2(√2)))ln(((2−(√2))/(2+(√2))))](Q99469.png)
$$\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\:=\mathrm{v}\:\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} −\mathrm{2}}\mathrm{dt}\:=−\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{2}} ^{\infty} \:\left(\frac{\mathrm{1}}{\mathrm{v}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{v}+\sqrt{\mathrm{2}}}\right)\mathrm{dv} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\frac{\mathrm{v}−\sqrt{\mathrm{2}}}{\mathrm{v}+\sqrt{\mathrm{2}}}\mid\right]_{\mathrm{2}} ^{\infty} \:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right) \\ $$
Commented by mathmax by abdo last updated on 20/Jun/20
![s =lim_(n→+∞) (1/n)Σ_(k=1) ^n ((√(k/n))/(1+((k/n))^2 )) =∫_0 ^(1 ) ((√x)/(1+x^2 )) dx =_((√x)=t) ∫_0 ^(1 ) (t/(1+t^4 ))(2t)dt =2 ∫_0 ^1 (t^2 /(1+t^4 ))dt but ∫_0 ^1 (t^2 /(1+t^4 )) =∫_0 ^1 (1/((1/t^2 )+t^2 )) dt =(1/2)∫_0 ^1 ((1+(1/t^2 )+1−(1/t^2 ))/(t^2 +(1/t^2 ))) dt =(1/2) ∫_0 ^1 ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt(t−(1/t)=−u) +(1/2)∫_0 ^1 ((1−(1/t^2 ))/((t+(1/t))^2 −2))(t+(1/t)=−v) =−(1/2)∫_0 ^∞ ((−du)/(u^2 +2)) −(1/2)∫_0 ^∞ ((−dv)/(v^2 −2)) =(1/2) ∫_0 ^∞ (du/(u^2 +2)) +(1/2)∫_0 ^∞ (dv/(v^2 −2)) we hsve ∫_0 ^∞ (du/(u^2 +2)) =_(u=(√2)α) ∫_0 ^∞ (((√2)dα)/(2(1+α^2 ))) =(1/(√2))×(π/2) =(π/(2(√2))) ∫_0 ^∞ (dv/(v^2 −2)) =(1/4)∫_0 ^∞ ((1/(v−2))−(1/(v+2)))dv =(1/4)[ln∣((v−2)/(v+2))∣]_0 ^∞ =(1/4)×0=0 ⇒ s =(π/(√2))](Q99386.png)
$$\mathrm{s}\:=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\:\:\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\:\frac{\sqrt{\frac{\mathrm{k}}{\mathrm{n}}}}{\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\frac{\sqrt{\mathrm{x}}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\:\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\left(\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\mathrm{dt}\:\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }+\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} \:+\mathrm{2}}\mathrm{dt}\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}=−\mathrm{u}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} −\mathrm{2}}\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}=−\mathrm{v}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{−\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{2}}\:\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{−\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}\:\mathrm{we}\:\mathrm{hsve} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{2}}\:=_{\mathrm{u}=\sqrt{\mathrm{2}}\alpha} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\sqrt{\mathrm{2}}\mathrm{d}\alpha}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{v}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{v}+\mathrm{2}}\right)\mathrm{dv}\:=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\mid\frac{\mathrm{v}−\mathrm{2}}{\mathrm{v}+\mathrm{2}}\mid\right]_{\mathrm{0}} ^{\infty} \:=\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{0}=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{s}\:=\frac{\pi}{\sqrt{\mathrm{2}}} \\ $$
Commented by Ar Brandon last updated on 21/Jun/20
$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{obtain}\:\mathrm{your}\:\mathrm{limits}\:\mathrm{for}\:\mathrm{v}? \\ $$$$\mathrm{I}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{was}\:\mathrm{supposed}\:\mathrm{to}\:\mathrm{range}\:\mathrm{from}\:\mathrm{2}\:\mathrm{to}\:−\infty \\ $$