
Question and Answers Forum
Question Number 99239 by abdomathmax last updated on 19/Jun/20
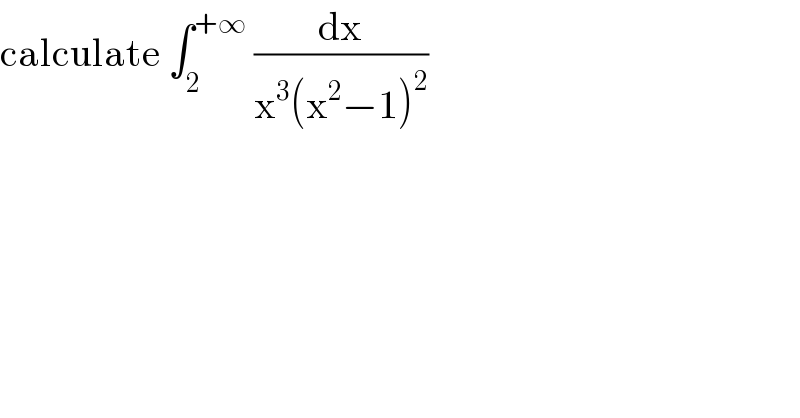
Answered by MJS last updated on 19/Jun/20
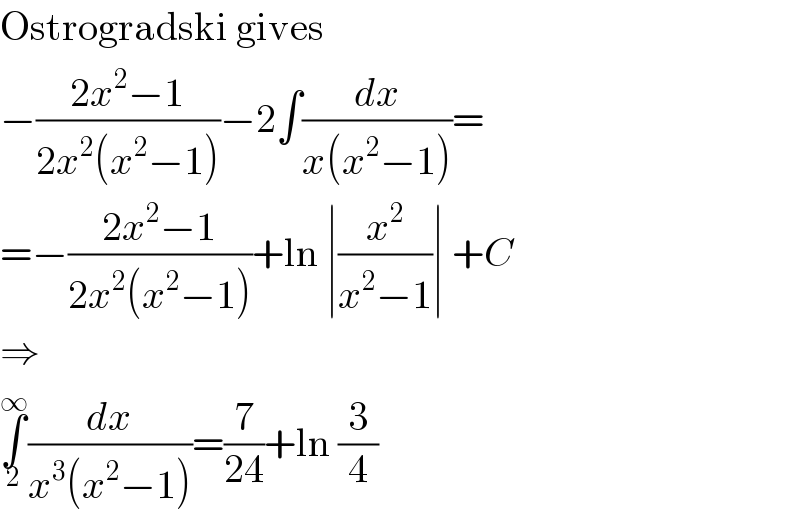
Commented by Ar Brandon last updated on 20/Jun/20
Hello Mr MJS,�� greetings to you Sir.
Commented by MJS last updated on 20/Jun/20
also back to you!
Answered by mathmax by abdo last updated on 21/Jun/20

