Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 99259 by DGmichael last updated on 19/Jun/20

Answered by abdomathmax last updated on 19/Jun/20

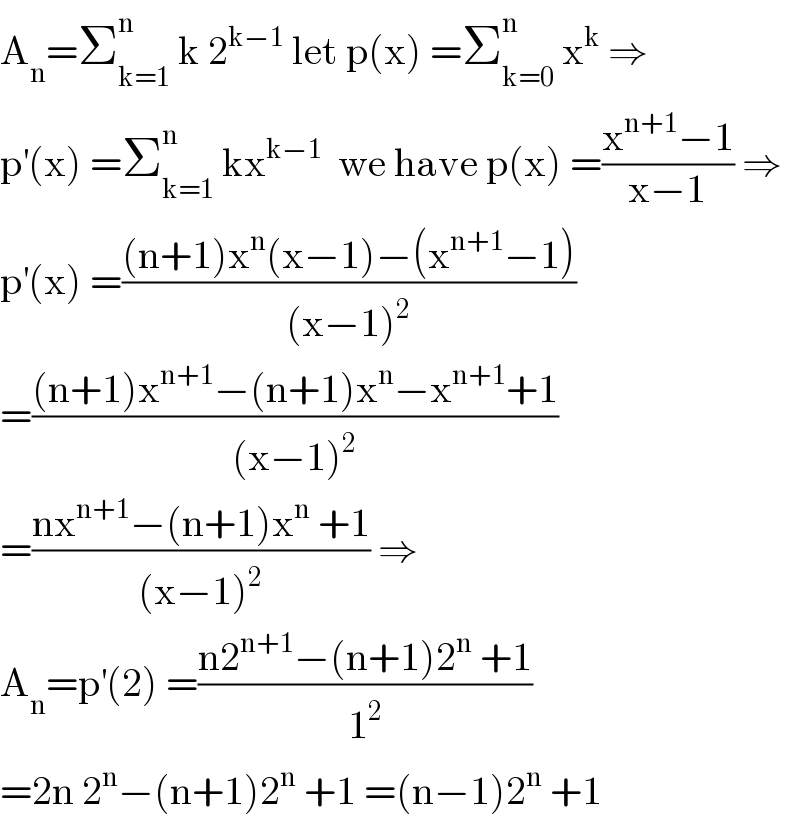
A_n =Σ_(k=1) ^n k 2^(k−1) let p(x) =Σ_(k=0) ^n x^k ⇒ p^′ (x) =Σ_(k=1) ^n kx^(k−1) we have p(x) =((x^(n+1) −1)/(x−1)) ⇒ p^′ (x) =(((n+1)x^n (x−1)−(x^(n+1) −1))/((x−1)^2 )) =(((n+1)x^(n+1) −(n+1)x^n −x^(n+1) +1)/((x−1)^2 )) =((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒ A_n =p^′ (2) =((n2^(n+1) −(n+1)2^n +1)/1^2 ) =2n 2^n −(n+1)2^n +1 =(n−1)2^n +1

$$\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}\:\mathrm{2}^{\mathrm{k}−\mathrm{1}} \:\mathrm{let}\:\mathrm{p}\left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{x}^{\mathrm{k}} \:\Rightarrow \\ $$$$\mathrm{p}^{'} \left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{kx}^{\mathrm{k}−\mathrm{1}} \:\:\mathrm{we}\:\mathrm{have}\:\mathrm{p}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{p}^{'} \left(\mathrm{x}\right)\:=\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} \left(\mathrm{x}−\mathrm{1}\right)−\left(\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{\mathrm{n}+\mathrm{1}} +\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$$$=\frac{\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} \:+\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\mathrm{p}^{'} \left(\mathrm{2}\right)\:=\frac{\mathrm{n2}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}} \:+\mathrm{1}}{\mathrm{1}^{\mathrm{2}} } \\ $$$$=\mathrm{2n}\:\mathrm{2}^{\mathrm{n}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}} \:+\mathrm{1}\:=\left(\mathrm{n}−\mathrm{1}\right)\mathrm{2}^{\mathrm{n}} \:+\mathrm{1} \\ $$

Commented by DGmichael last updated on 19/Jun/20

thanks sir !

Answered by mr W last updated on 19/Jun/20

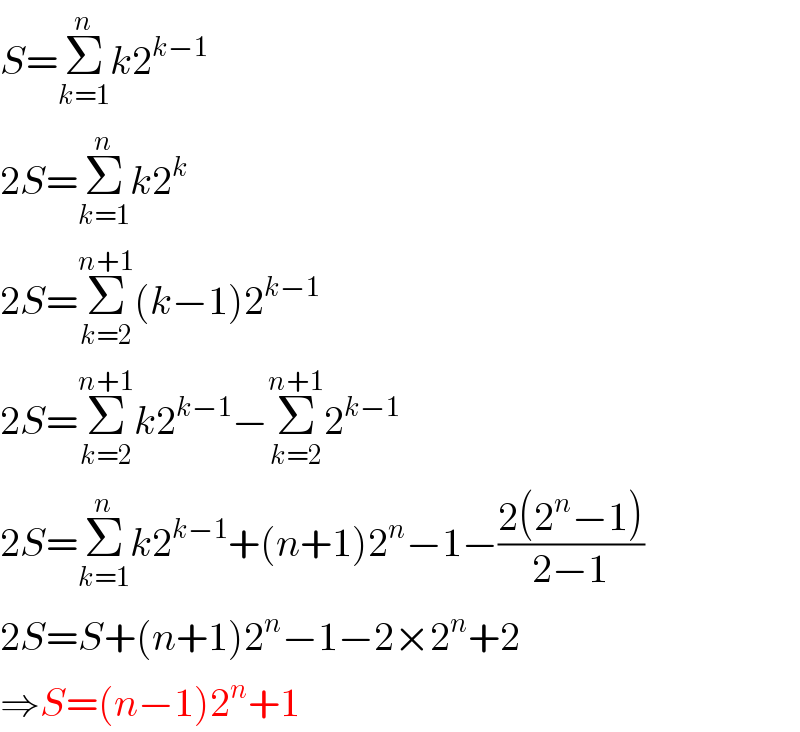
S=Σ_(k=1) ^n k2^(k−1) 2S=Σ_(k=1) ^n k2^k 2S=Σ_(k=2) ^(n+1) (k−1)2^(k−1) 2S=Σ_(k=2) ^(n+1) k2^(k−1) −Σ_(k=2) ^(n+1) 2^(k−1) 2S=Σ_(k=1) ^n k2^(k−1) +(n+1)2^n −1−((2(2^n −1))/(2−1)) 2S=S+(n+1)2^n −1−2×2^n +2 ⇒S=(n−1)2^n +1

$${S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}−\mathrm{1}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}\left({k}−\mathrm{1}\right)\mathrm{2}^{{k}−\mathrm{1}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{k}\mathrm{2}^{{k}−\mathrm{1}} −\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}\mathrm{2}^{{k}−\mathrm{1}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}−\mathrm{1}} +\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}} −\mathrm{1}−\frac{\mathrm{2}\left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}−\mathrm{1}} \\ $$$$\mathrm{2}{S}={S}+\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}} −\mathrm{1}−\mathrm{2}×\mathrm{2}^{{n}} +\mathrm{2} \\ $$$$\Rightarrow{S}=\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}} +\mathrm{1} \\ $$

Commented by Ar Brandon last updated on 20/Jun/20

Cool, I erred��

Commented by DGmichael last updated on 20/Jun/20

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com