Question Number 99260 by Ar Brandon last updated on 19/Jun/20
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation}\: \\ $$$$\mathrm{xy}'−\mathrm{y}+\frac{\mathrm{2x}+\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$
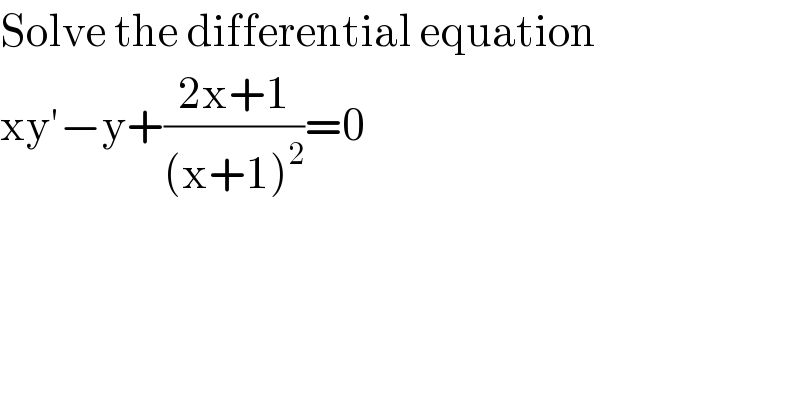
Answered by Mr.D.N. last updated on 19/Jun/20
Commented by Ar Brandon last updated on 20/Jun/20
Thank you ��
Answered by mathmax by abdo last updated on 19/Jun/20
![xy^′ −y +((2x+1)/((x+1)^2 )) =0 (he)→xy^′ −y =0 ⇒(y^′ /y) =(1/x) ⇒ln∣y∣ =ln∣x∣ +c ⇒ y(x) =k ∣x∣ let determine slution on ]0,+∞[ ⇒y(x) =kx mvc method →y^′ =k^′ x +k (e) ⇒k^′ x^2 +kx −kx =−((2x+1)/((x+1)^2 )) ⇒k^′ =−((2x+1)/(x^2 (x+1)^2 )) ⇒k(x) =−∫((2x+1)/(x^2 (x+1)^2 ))dx +c let decompose F(x) =((2x+1)/(x^2 (x+1)^2 )) we have (1/x^2 )−(1/((x+1)^2 )) =(((x+1)^2 −x^2 )/(x^2 (x+1)^2 )) =((2x+1)/(x^2 (x+1)^2 )) =F(x) ⇒k(x) =−∫(dx/x^2 ) +∫ (dx/((x+1)^2 )) =(1/x)−(1/(x+1)) +c ⇒ y(x) =xk(x) =x((1/x)−(1/(x+1)) +c) =1−(x/(x+1)) +c =(1/(x+1)) +c](Q99279.png)
$$\mathrm{xy}^{'} \:−\mathrm{y}\:+\frac{\mathrm{2x}+\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{0}\:\:\left(\mathrm{he}\right)\rightarrow\mathrm{xy}^{'} −\mathrm{y}\:=\mathrm{0}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=\frac{\mathrm{1}}{\mathrm{x}}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=\mathrm{ln}\mid\mathrm{x}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\left.\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{k}\:\mid\mathrm{x}\mid\:\:\mathrm{let}\:\mathrm{determine}\:\mathrm{slution}\:\mathrm{on}\:\right]\mathrm{0},+\infty\left[\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{kx}\right. \\ $$$$\mathrm{mvc}\:\:\mathrm{method}\:\rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{x}\:+\mathrm{k} \\ $$$$\left(\mathrm{e}\right)\:\Rightarrow\mathrm{k}^{'} \:\mathrm{x}^{\mathrm{2}} \:+\mathrm{kx}\:−\mathrm{kx}\:=−\frac{\mathrm{2x}+\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{k}^{'} \:=−\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{k}\left(\mathrm{x}\right)\:=−\int\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:+\mathrm{c} \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{F}\left(\mathrm{x}\right)\:\Rightarrow\mathrm{k}\left(\mathrm{x}\right)\:=−\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} }\:+\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{xk}\left(\mathrm{x}\right)\:=\mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\mathrm{c}\right)\:=\mathrm{1}−\frac{\mathrm{x}}{\mathrm{x}+\mathrm{1}}\:+\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\mathrm{c} \\ $$
Commented by mathmax by abdo last updated on 19/Jun/20
$$\mathrm{sorry}\:\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\mathrm{cx} \\ $$
Commented by Ar Brandon last updated on 20/Jun/20
Thanks
Commented by mathmax by abdo last updated on 20/Jun/20
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$