
Question Number 99351 by 659083337 last updated on 20/Jun/20
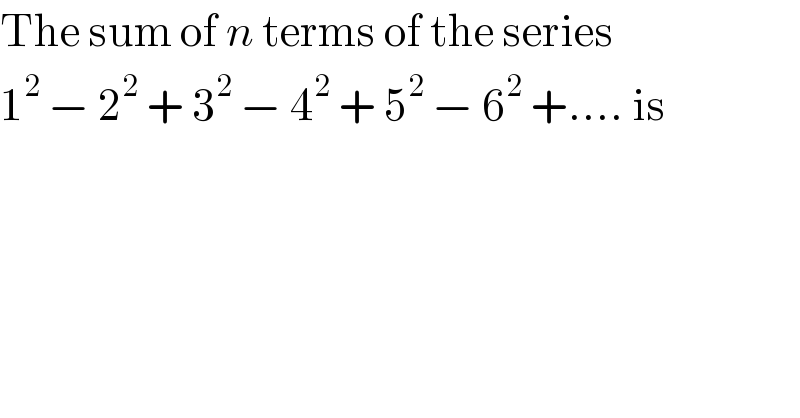
$$\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:{n}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{series}\: \\ $$$$\mathrm{1}^{\mathrm{2}} \:−\:\mathrm{2}^{\mathrm{2}} \:+\:\mathrm{3}^{\mathrm{2}} \:−\:\mathrm{4}^{\mathrm{2}} \:+\:\mathrm{5}^{\mathrm{2}} \:−\:\mathrm{6}^{\mathrm{2}} \:+....\:\mathrm{is} \\ $$
Commented by I want to learn more last updated on 20/Jun/20
![1^2 + 3^2 + 5^2 + ... − 2^2 − 4^2 − 6^2 − ... 1^2 + 3^2 + 5^2 + ... to n terms − (2^2 + 4^2 + 6^2 + ... to n terms) = 1^2 + 3^2 + 5^2 + ... + (2n − 1)^2 − [2^2 + 4^2 + 6^2 + ... (2n)^2 ] = (n/3)(4n^2 − 1) − ((2n(n + 1)(2n + 1))/3) = (n/3)[(4n^2 − 1) − 2(n + 1)(2n + 1)] = (n/3)[4n^2 − 1 − (4n^2 + 6n + 2)] = (n/3)(4n^2 − 1 − 4n^2 − 6n − 2) = (n/3)(− 6n − 3) , ⇒ − ((3n)/3)(2n + 1) Therefore, 1^2 − 2^2 + 3^2 − 4^2 + 5^2 − 6^2 + .... = − (2n^2 + n)](Q99393.png)
$$\mathrm{1}^{\mathrm{2}} \:+\:\mathrm{3}^{\mathrm{2}} \:+\:\mathrm{5}^{\mathrm{2}} \:+\:...\:−\:\mathrm{2}^{\mathrm{2}} \:\:−\:\:\mathrm{4}^{\mathrm{2}} \:\:−\:\:\mathrm{6}^{\mathrm{2}} \:\:−\:\:... \\ $$$$\:\:\:\:\:\:\:\mathrm{1}^{\mathrm{2}} \:+\:\mathrm{3}^{\mathrm{2}} \:+\:\mathrm{5}^{\mathrm{2}} \:+\:...\:\mathrm{to}\:\mathrm{n}\:\mathrm{terms}\:\:−\:\left(\mathrm{2}^{\mathrm{2}} \:\:+\:\:\mathrm{4}^{\mathrm{2}} \:\:+\:\:\mathrm{6}^{\mathrm{2}} \:\:+\:\:...\:\:\mathrm{to}\:\:\mathrm{n}\:\mathrm{terms}\right) \\ $$$$\:\:\:\:\:=\:\:\:\:\:\mathrm{1}^{\mathrm{2}} \:+\:\mathrm{3}^{\mathrm{2}} \:+\:\mathrm{5}^{\mathrm{2}} \:+\:...\:+\:\:\left(\mathrm{2n}\:\:−\:\:\mathrm{1}\right)^{\mathrm{2}} \:\:−\:\left[\mathrm{2}^{\mathrm{2}} \:\:+\:\:\mathrm{4}^{\mathrm{2}} \:\:+\:\:\mathrm{6}^{\mathrm{2}} \:\:+\:\:...\:\:\left(\mathrm{2n}\right)^{\mathrm{2}} \right] \\ $$$$\:\:=\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{n}}{\mathrm{3}}\left(\mathrm{4n}^{\mathrm{2}} \:−\:\:\mathrm{1}\right)\:\:−\:\:\frac{\mathrm{2n}\left(\mathrm{n}\:\:+\:\:\mathrm{1}\right)\left(\mathrm{2n}\:\:+\:\:\mathrm{1}\right)}{\mathrm{3}} \\ $$$$\:\:=\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{n}}{\mathrm{3}}\left[\left(\mathrm{4n}^{\mathrm{2}} \:−\:\:\mathrm{1}\right)\:\:−\:\:\mathrm{2}\left(\mathrm{n}\:\:+\:\:\mathrm{1}\right)\left(\mathrm{2n}\:\:+\:\:\mathrm{1}\right)\right] \\ $$$$\:\:=\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{n}}{\mathrm{3}}\left[\mathrm{4n}^{\mathrm{2}} \:−\:\:\mathrm{1}\:\:−\:\:\left(\mathrm{4n}^{\mathrm{2}} \:\:+\:\:\mathrm{6n}\:\:+\:\:\mathrm{2}\right)\right] \\ $$$$\:\:=\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{n}}{\mathrm{3}}\left(\mathrm{4n}^{\mathrm{2}} \:−\:\:\mathrm{1}\:\:−\:\:\mathrm{4n}^{\mathrm{2}} \:\:−\:\:\mathrm{6n}\:\:−\:\:\mathrm{2}\right) \\ $$$$\:\:=\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{n}}{\mathrm{3}}\left(−\:\:\mathrm{6n}\:\:−\:\:\mathrm{3}\right)\:,\:\:\:\:\:\:\Rightarrow\:\:\:\:\:−\:\frac{\mathrm{3n}}{\mathrm{3}}\left(\mathrm{2n}\:\:+\:\:\mathrm{1}\right) \\ $$$$\mathrm{Therefore}, \\ $$$$\mathrm{1}^{\mathrm{2}} \:\:−\:\:\:\mathrm{2}^{\mathrm{2}} \:\:+\:\:\:\mathrm{3}^{\mathrm{2}} \:\:\:−\:\:\mathrm{4}^{\mathrm{2}} \:\:\:+\:\:\mathrm{5}^{\mathrm{2}} \:\:−\:\:\mathrm{6}^{\mathrm{2}} \:\:+\:\:....\:\:\:\:=\:\:\:−\:\:\left(\mathrm{2n}^{\mathrm{2}} \:\:+\:\:\mathrm{n}\right) \\ $$
Commented by PRITHWISH SEN 2 last updated on 20/Jun/20
![If n is even then the series becomes (1^2 −2^2 )+(3^2 −4^2 )+......+[(n−3)^2 −(n−2)^2 ]+ [(n−1)^2 −n^2 ] = −{3+7+......(2n−5)+(2n−1)} it is an A.P with commn diff. 4 and no of terms = (n/2) then S_(n/2) = −(n/4){2.3+((n/2)−1)4}= − ((n(n+1))/2) now when n is odd then the series = 1^2 +(3^2 −2^2 )+.......+{(n−2)^2 −(n−3)^2 }+ {n^2 −(n−1)^2 } = 1+5+9+......+(2n−5)+(2n−1) it is also an A.P where d=4 and no. of term=((n+1)/2) then S_((n+1)/2) = ((n+1)/4){2.1+(((n+1)/2) −1)4} = ((n(n+1))/2) i.e S_n = (−1)^(n+1) .((n(n+1))/2) now when n=5 1^2 −2^2 +3^2 −4^2 +5^2 = (−1)^6 .((5×6)/2)=15 when n=6 1^2 −2^2 +3^2 −4^2 +5^2 −6^2 =(−1)^7 .((6×7)/2)=−21 please check](Q99409.png)
$$\mathrm{If}\:\boldsymbol{\mathrm{n}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{even}}\:\boldsymbol{\mathrm{then}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{series}}\:\boldsymbol{\mathrm{becomes}} \\ $$$$\left(\mathrm{1}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \right)+\left(\mathrm{3}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} \right)+......+\left[\left(\boldsymbol{\mathrm{n}}−\mathrm{3}\right)^{\mathrm{2}} −\left(\boldsymbol{\mathrm{n}}−\mathrm{2}\right)^{\mathrm{2}} \right]+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\left(\boldsymbol{\mathrm{n}}−\mathrm{1}\right)^{\mathrm{2}} −\boldsymbol{\mathrm{n}}^{\mathrm{2}} \right] \\ $$$$=\:−\left\{\mathrm{3}+\mathrm{7}+......\left(\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{5}\right)+\left(\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}\right)\right\} \\ $$$$\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{an}}\:\boldsymbol{\mathrm{A}}.\boldsymbol{\mathrm{P}}\:\boldsymbol{\mathrm{with}}\:\boldsymbol{\mathrm{commn}}\:\boldsymbol{\mathrm{diff}}.\:\mathrm{4}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{no}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{terms}} \\ $$$$=\:\frac{\boldsymbol{\mathrm{n}}}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{then}} \\ $$$$\boldsymbol{\mathrm{S}}_{\frac{\boldsymbol{\mathrm{n}}}{\mathrm{2}}} =\:−\frac{\boldsymbol{\mathrm{n}}}{\mathrm{4}}\left\{\mathrm{2}.\mathrm{3}+\left(\frac{\boldsymbol{\mathrm{n}}}{\mathrm{2}}−\mathrm{1}\right)\mathrm{4}\right\}=\:−\:\frac{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{now}}\:\boldsymbol{\mathrm{when}}\:\boldsymbol{\mathrm{n}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{odd}}\:\boldsymbol{\mathrm{then}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{series}} \\ $$$$=\:\mathrm{1}^{\mathrm{2}} +\left(\mathrm{3}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \right)+.......+\left\{\left(\mathrm{n}−\mathrm{2}\right)^{\mathrm{2}} −\left(\mathrm{n}−\mathrm{3}\right)^{\mathrm{2}} \right\}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\mathrm{n}^{\mathrm{2}} −\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{2}} \right\} \\ $$$$=\:\mathrm{1}+\mathrm{5}+\mathrm{9}+......+\left(\mathrm{2n}−\mathrm{5}\right)+\left(\mathrm{2n}−\mathrm{1}\right) \\ $$$$\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{also}}\:\boldsymbol{\mathrm{an}}\:\boldsymbol{\mathrm{A}}.\boldsymbol{\mathrm{P}}\:\boldsymbol{\mathrm{where}} \\ $$$$\boldsymbol{\mathrm{d}}=\mathrm{4}\:\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{no}}.\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{term}}=\frac{\boldsymbol{\mathrm{n}}+\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{then}} \\ $$$$\boldsymbol{\mathrm{S}}_{\frac{\boldsymbol{\mathrm{n}}+\mathrm{1}}{\mathrm{2}}} =\:\frac{\boldsymbol{\mathrm{n}}+\mathrm{1}}{\mathrm{4}}\left\{\mathrm{2}.\mathrm{1}+\left(\frac{\boldsymbol{\mathrm{n}}+\mathrm{1}}{\mathrm{2}}\:−\mathrm{1}\right)\mathrm{4}\right\}\:=\:\frac{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{i}}.\boldsymbol{\mathrm{e}}\:\boldsymbol{\mathrm{S}}_{\boldsymbol{\mathrm{n}}} =\:\left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}+\mathrm{1}} .\frac{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{now}}\:\boldsymbol{\mathrm{when}}\:\boldsymbol{\mathrm{n}}=\mathrm{5} \\ $$$$\mathrm{1}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \:=\:\left(−\mathrm{1}\right)^{\mathrm{6}} .\frac{\mathrm{5}×\mathrm{6}}{\mathrm{2}}=\mathrm{15} \\ $$$$\boldsymbol{\mathrm{when}}\:\boldsymbol{\mathrm{n}}=\mathrm{6} \\ $$$$\mathrm{1}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} −\mathrm{6}^{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{7}} .\frac{\mathrm{6}×\mathrm{7}}{\mathrm{2}}=−\mathrm{21} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$
Commented by Dwaipayan Shikari last updated on 20/Jun/20
Yes sir it is right
Commented by I want to learn more last updated on 20/Jun/20

$$\mathrm{sir},\:\mathrm{please}\:\mathrm{use}\:\mathrm{your}\:\:\mathrm{nth}\:\mathrm{term}\:\mathrm{to}\:\mathrm{show}\:\mathrm{few}\:\mathrm{sum}. \\ $$$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{it}. \\ $$
Commented by I want to learn more last updated on 20/Jun/20

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
