Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 99541 by student work last updated on 21/Jun/20

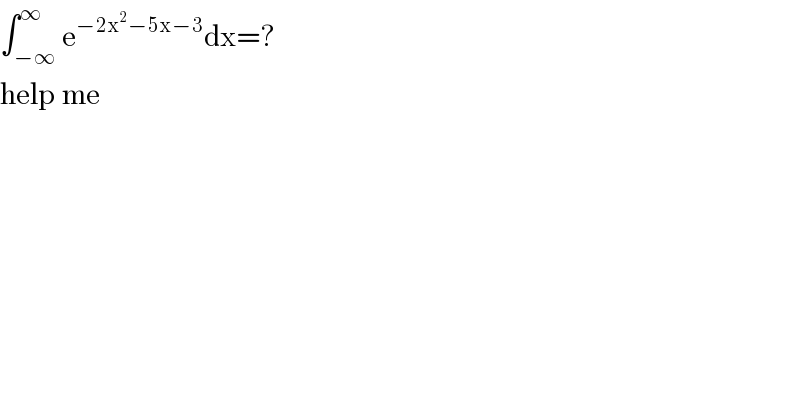
∫_(−∞) ^∞ e^(−2x^2 −5x−3) dx=? help me

$$\int_{−\infty} ^{\infty} \mathrm{e}^{−\mathrm{2x}^{\mathrm{2}} −\mathrm{5x}−\mathrm{3}} \mathrm{dx}=?\: \\ $$$$\mathrm{help}\:\mathrm{me} \\ $$

Answered by smridha last updated on 21/Jun/20

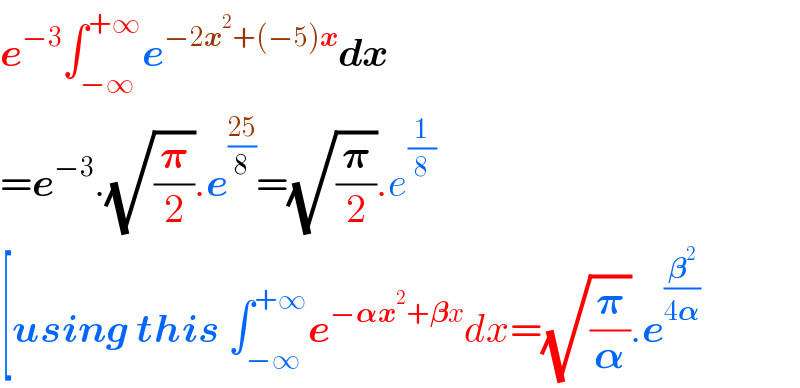
e^(−3) ∫_(−∞) ^(+∞) e^(−2x^2 +(−5)x) dx =e^(−3) .(√(𝛑/2)).e^((25)/8) =(√(𝛑/2)).e^(1/8) [using this ∫_(−∞) ^(+∞) e^(−𝛂x^2 +𝛃x) dx=(√(𝛑/𝛂)).e^(𝛃^2 /(4𝛂))

$$\boldsymbol{{e}}^{−\mathrm{3}} \int_{−\infty} ^{+\infty} \boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\left(−\mathrm{5}\right)\boldsymbol{{x}}} \boldsymbol{{dx}} \\ $$$$=\boldsymbol{{e}}^{−\mathrm{3}} .\sqrt{\frac{\boldsymbol{\pi}}{\mathrm{2}}}.\boldsymbol{{e}}^{\frac{\mathrm{25}}{\mathrm{8}}} =\sqrt{\frac{\boldsymbol{\pi}}{\mathrm{2}}}.{e}^{\frac{\mathrm{1}}{\mathrm{8}}} \\ $$$$\left[\boldsymbol{{using}}\:\boldsymbol{{this}}\:\int_{−\infty} ^{+\infty} \boldsymbol{{e}}^{−\boldsymbol{\alpha{x}}^{\mathrm{2}} +\boldsymbol{\beta}{x}} {dx}=\sqrt{\frac{\boldsymbol{\pi}}{\boldsymbol{\alpha}}}.\boldsymbol{{e}}^{\frac{\boldsymbol{\beta}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{\alpha}}} \:\right. \\ $$

Commented by student work last updated on 21/Jun/20

thanks sir good

$$\mathrm{thanks}\:\mathrm{sir}\:\mathrm{good} \\ $$

Commented by smridha last updated on 21/Jun/20

welcome

Answered by aleks041103 last updated on 21/Jun/20

I=∫_(−∞) ^∞ e^(−2x^2 −5x−3) dx= =∫_(−∞) ^∞ e^(−(2x^2 +5x+3)) dx We complete the square: 2x^2 +5x+3= =((√2)x)^2 +2((√2)x)(5/(2(√2)))+((5/(2(√2))))^2 −((5/(2(√2))))^2 +3= =((√2)x+(5/(2(√2))))^2 +3−((25)/8)= =((√2)x+(5/(2(√2))))^2 −(1/8) Let u=(√2)x+(5/(2(√2))) ⇒du=(√2) dx ⇒ dx=(du/(√2)) Also x→+∞ ⇒ u→+∞ x→−∞ ⇒ u→−∞ Then I=∫_(−∞) ^(+∞) e^(−(u^2 −1/8)) (du/(√2))=(e^(1/8) /(√2))∫_(−∞) ^(+∞) e^(−u^2 ) du But ∫_(−∞) ^(+∞) e^(−u^2 ) du=(√π) is the gaussian integral. Then for I we have: I=e^(1/8) (√(π/2)) Or: I=∫_(−∞) ^∞ e^(−2x^2 −5x−3) dx=e^(1/8) (√(π/2))

$${I}=\int_{−\infty} ^{\infty} \mathrm{e}^{−\mathrm{2x}^{\mathrm{2}} −\mathrm{5x}−\mathrm{3}} \mathrm{dx}= \\ $$$$=\int_{−\infty} ^{\infty} \mathrm{e}^{−\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{5x}+\mathrm{3}\right)} \mathrm{dx} \\ $$$${We}\:{complete}\:{the}\:{square}: \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{3}= \\ $$$$=\left(\sqrt{\mathrm{2}}{x}\right)^{\mathrm{2}} +\mathrm{2}\left(\sqrt{\mathrm{2}}{x}\right)\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{2}}}+\left(\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{3}= \\ $$$$=\left(\sqrt{\mathrm{2}}{x}+\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{3}−\frac{\mathrm{25}}{\mathrm{8}}= \\ $$$$=\left(\sqrt{\mathrm{2}}{x}+\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${Let} \\ $$$${u}=\sqrt{\mathrm{2}}{x}+\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow{du}=\sqrt{\mathrm{2}}\:{dx}\:\Rightarrow\:{dx}=\frac{{du}}{\sqrt{\mathrm{2}}} \\ $$$${Also}\: \\ $$$${x}\rightarrow+\infty\:\Rightarrow\:{u}\rightarrow+\infty \\ $$$${x}\rightarrow−\infty\:\Rightarrow\:{u}\rightarrow−\infty \\ $$$${Then} \\ $$$${I}=\int_{−\infty} ^{+\infty} {e}^{−\left({u}^{\mathrm{2}} −\mathrm{1}/\mathrm{8}\right)} \frac{{du}}{\sqrt{\mathrm{2}}}=\frac{{e}^{\mathrm{1}/\mathrm{8}} }{\sqrt{\mathrm{2}}}\int_{−\infty} ^{+\infty} {e}^{−{u}^{\mathrm{2}} } {du} \\ $$$${But}\:\int_{−\infty} ^{+\infty} {e}^{−{u}^{\mathrm{2}} } {du}=\sqrt{\pi}\:{is}\:{the}\:{gaussian} \\ $$$${integral}.\:{Then}\:{for}\:{I}\:{we}\:{have}: \\ $$$${I}={e}^{\mathrm{1}/\mathrm{8}} \sqrt{\frac{\pi}{\mathrm{2}}} \\ $$$${Or}: \\ $$$${I}=\int_{−\infty} ^{\infty} \mathrm{e}^{−\mathrm{2x}^{\mathrm{2}} −\mathrm{5x}−\mathrm{3}} \mathrm{dx}={e}^{\mathrm{1}/\mathrm{8}} \sqrt{\frac{\pi}{\mathrm{2}}} \\ $$

Commented by student work last updated on 21/Jun/20

thanks sir

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Answered by mathmax by abdo last updated on 21/Jun/20

I =∫_(−∞) ^(+∞) e^(−2x^2 −5x−3) dx ⇒ I =∫_(−∞) ^(+∞) e^(−2{ x^2 +(5/2)x+(3/2)}) dx =∫_(−∞) ^(+∞) e^(−2{ x^2 +2.(5/4)x +((25)/(16))+(3/2)−((25)/(16))}) dx =∫_(−∞) ^(+∞ ) e^(−2{(x+(5/4))^2 −(1/(16))}) dx (x+(5/4))(√2)=u =e^(1/8) ∫_(−∞) ^(+∞) e^(−u^2 ) (du/(√2)) =(e^(1/8) /(√2))×(√π) ⇒I =^8 (√e)×(√(π/2))

$$\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{2x}^{\mathrm{2}} −\mathrm{5x}−\mathrm{3}} \mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{2}\left\{\:\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{2}}\mathrm{x}+\frac{\mathrm{3}}{\mathrm{2}}\right\}} \:\mathrm{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{2}\left\{\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}.\frac{\mathrm{5}}{\mathrm{4}}\mathrm{x}\:+\frac{\mathrm{25}}{\mathrm{16}}+\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{25}}{\mathrm{16}}\right\}} \mathrm{dx}\:=\int_{−\infty} ^{+\infty\:} \mathrm{e}^{−\mathrm{2}\left\{\left(\mathrm{x}+\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} \:−\frac{\mathrm{1}}{\mathrm{16}}\right\}} \mathrm{dx}\:\:\left(\mathrm{x}+\frac{\mathrm{5}}{\mathrm{4}}\right)\sqrt{\mathrm{2}}=\mathrm{u} \\ $$$$=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{8}}} \:\int_{−\infty} ^{+\infty} \:\:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \:\frac{\mathrm{du}}{\sqrt{\mathrm{2}}}\:=\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{8}}} }{\sqrt{\mathrm{2}}}×\sqrt{\pi}\:\Rightarrow\mathrm{I}\:=^{\mathrm{8}} \sqrt{\mathrm{e}}×\sqrt{\frac{\pi}{\mathrm{2}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com