
Question and Answers Forum
Question Number 99623 by hardylanes last updated on 22/Jun/20

Commented by Dwaipayan Shikari last updated on 22/Jun/20
![=(((1−i)^(2.2) )/(4^3 ((1/2)+((√3)/2)i)^3 ))=(((−2i)^2 )/(64e^(((πi)/3).3) ))=((−4)/(64 e^(πi) ))=((−4)/(−64))=(1/(16))+0.i=z mod (z) is (1/(16)) arg(z) is 0 [As α=tan^(−1) ((0/(1/(16))))=0 ]{And e^(πi) =−1}](Q99635.png)
Answered by Rio Michael last updated on 22/Jun/20
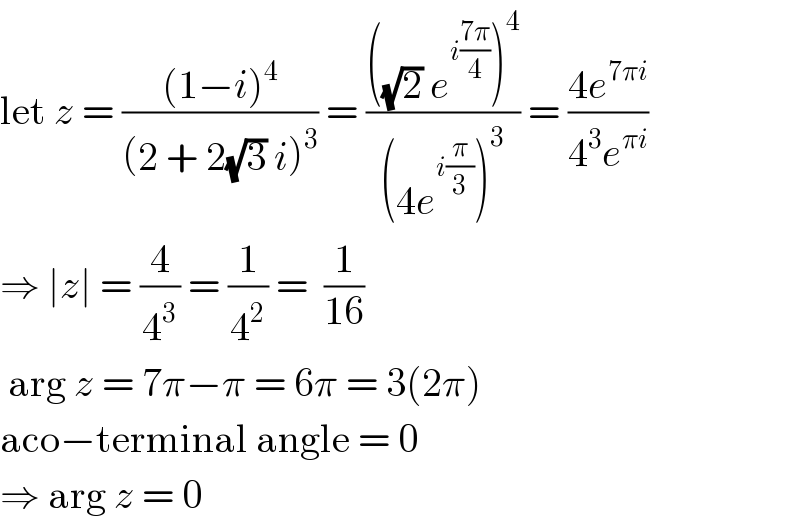
Commented by mathmax by abdo last updated on 23/Jun/20
![z =(((1−i)^4 )/((2+2(√3)i)^3 )) we have 1−i =(√2)e^(−((iπ)/4)) ⇒(1−i)^4 =4 e^(−iπ) 2+2(√3)i =2(1+(√3)i) =4((1/2)+((i(√3))/2)) =4e^((iπ)/3) ⇒(2+2(√3)i)^3 =4^3 e^((4iπ)/3) ⇒ z =(1/(16)) e^(−iπ−((4iπ)/3)) =(1/(16)) e^(−i(π+((4π)/3))) =(1/(16)) e^(−i(((7π)/3))) =(1/(16)) e^(−i(2π +(π/3))) =(1/(16)) e^(−((iπ)/3)) ⇒ ∣z∣ =(1/(16)) and argz ≡−(π/3)[2π]](Q99787.png)
