Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 99685 by Ar Brandon last updated on 22/Jun/20

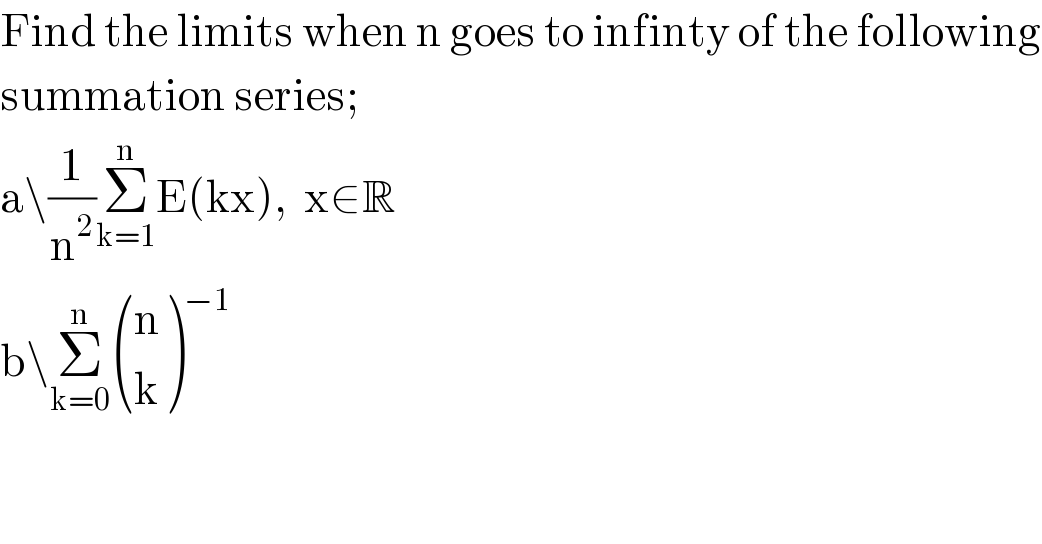
Find the limits when n goes to infinty of the following summation series; a\(1/n^2 )Σ_(k=1) ^n E(kx), x∈R b\Σ_(k=0) ^n ((n),(k) )^(−1)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{limits}\:\mathrm{when}\:\mathrm{n}\:\mathrm{goes}\:\mathrm{to}\:\mathrm{infinty}\:\mathrm{of}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{summation}\:\mathrm{series}; \\ $$$$\mathrm{a}\backslash\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{E}\left(\mathrm{kx}\right),\:\:\mathrm{x}\in\mathbb{R} \\ $$$$\mathrm{b}\backslash\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}^{−\mathrm{1}} \\ $$

Commented by Rasheed.Sindhi last updated on 22/Jun/20

To Tinku tara, the developer Sir, I don′t receive noticication at the moment.

$${To}\:\mathcal{T}{inku}\:{tara},\:{the}\:{developer} \\ $$$${Sir}, \\ $$$${I}\:{don}'{t}\:{receive}\:{noticication}\:{at}\:{the} \\ $$$${moment}. \\ $$

Commented by Tinku Tara last updated on 23/Jun/20

Are u logged on to more than one device? logout and login again from the device to receive notification again.

$$\mathrm{Are}\:\mathrm{u}\:\mathrm{logged}\:\mathrm{on}\:\mathrm{to}\:\mathrm{more}\:\mathrm{than}\:\mathrm{one} \\ $$$$\mathrm{device}?\:\mathrm{logout}\:\mathrm{and}\:\mathrm{login}\:\mathrm{again} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{device}\:\mathrm{to}\:\mathrm{receive} \\ $$$$\mathrm{notification}\:\mathrm{again}. \\ $$

Commented by Rasheed.Sindhi last updated on 23/Jun/20

Thanks sir After this complaint I received the notification of your reply. It seems that the problem was temporary....I used only one device.

$${Thanks}\:{sir} \\ $$$${After}\:{this}\:{complaint}\:{I}\:{received} \\ $$$${the}\:{notification}\:{of}\:{your}\:{reply}. \\ $$$${It}\:{seems}\:{that}\:{the}\:{problem}\:{was} \\ $$$${temporary}....{I}\:{used}\:{only}\:{one} \\ $$$${device}. \\ $$

Answered by maths mind last updated on 22/Jun/20

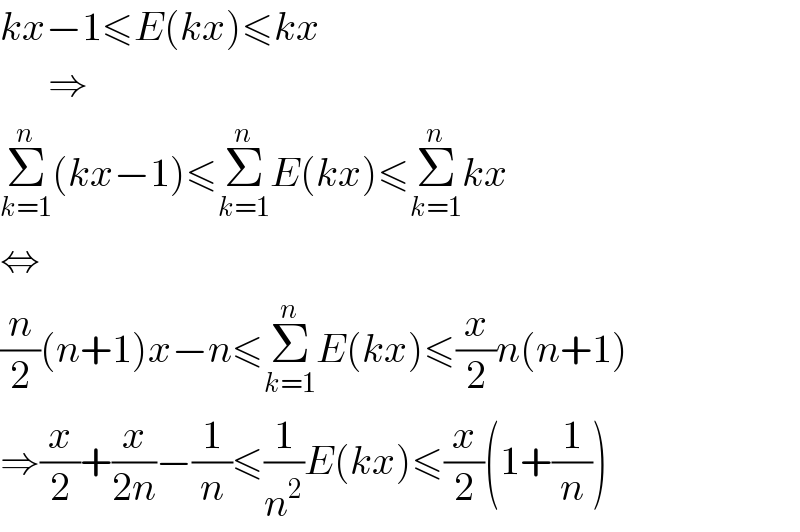
kx−1≤E(kx)≤kx ⇒ Σ_(k=1) ^n (kx−1)≤Σ_(k=1) ^n E(kx)≤Σ_(k=1) ^n kx ⇔ (n/2)(n+1)x−n≤Σ_(k=1) ^n E(kx)≤(x/2)n(n+1) ⇒(x/2)+(x/(2n))−(1/n)≤(1/n^2 )E(kx)≤(x/2)(1+(1/n))

$${kx}−\mathrm{1}\leqslant{E}\left({kx}\right)\leqslant{kx} \\ $$$$\:\:\:\:\:\:\Rightarrow \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({kx}−\mathrm{1}\right)\leqslant\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{E}\left({kx}\right)\leqslant\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{kx} \\ $$$$\Leftrightarrow \\ $$$$\frac{{n}}{\mathrm{2}}\left({n}+\mathrm{1}\right){x}−{n}\leqslant\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{E}\left({kx}\right)\leqslant\frac{{x}}{\mathrm{2}}{n}\left({n}+\mathrm{1}\right) \\ $$$$\Rightarrow\frac{{x}}{\mathrm{2}}+\frac{{x}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{{n}}\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{2}} }{E}\left({kx}\right)\leqslant\frac{{x}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right) \\ $$

Commented by Ar Brandon last updated on 22/Jun/20

Thanks ��

Answered by maths mind last updated on 22/Jun/20

lim_(n→ ∞) Σ_(k=0) ^n ((n),(k) )^− ?

$$\underset{{n}\rightarrow\:\infty} {\mathrm{lim}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{−} \:\:\:? \\ $$

Commented by Ar Brandon last updated on 22/Jun/20

I think it′s ^n C_k

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\:\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{k}} \: \\ $$

Answered by mathmax by abdo last updated on 22/Jun/20

a) S_n =(1/n^2 ) Σ_(k=1) ^n [kx] we have [kx] ≤kx<[kx]+1 ⇒kx−1<[kx]≤kx ⇒Σ_(k=1) ^n (kx−1)<Σ_(k=1) ^n [kx]≤Σ_(k=1) ^n (kx) ⇒((xn(n+1))/2)−n<Σ_(k=1) ^n [kx]≤((xn(n+1))/2) ((n(n+1))/(2n^2 ))x−(1/n)<(1/n^2 )Σ_(k=1) ^n [kx]≤((n(n+1))/(2n))x we passe to limit we get lim_(n→+∞) S_n =(x/2)

$$\left.\mathrm{a}\right)\:\:\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left[\mathrm{kx}\right]\:\:\mathrm{we}\:\mathrm{have}\:\:\:\left[\mathrm{kx}\right]\:\leqslant\mathrm{kx}<\left[\mathrm{kx}\right]+\mathrm{1}\:\Rightarrow\mathrm{kx}−\mathrm{1}<\left[\mathrm{kx}\right]\leqslant\mathrm{kx} \\ $$$$\:\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{kx}−\mathrm{1}\right)<\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left[\mathrm{kx}\right]\leqslant\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{kx}\right)\:\Rightarrow\frac{\mathrm{xn}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}−\mathrm{n}<\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left[\mathrm{kx}\right]\leqslant\frac{\mathrm{xn}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2n}^{\mathrm{2}} }\mathrm{x}−\frac{\mathrm{1}}{\mathrm{n}}<\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left[\mathrm{kx}\right]\leqslant\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2n}}\mathrm{x}\:\:\mathrm{we}\:\mathrm{passe}\:\mathrm{to}\:\mathrm{limit}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{S}_{\mathrm{n}} =\frac{\mathrm{x}}{\mathrm{2}} \\ $$

Commented by Ar Brandon last updated on 22/Jun/20

Thank you Sir ��

Commented by mathmax by abdo last updated on 23/Jun/20

you are welcome

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com