
Question and Answers Forum
Question Number 99824 by mathmax by abdo last updated on 23/Jun/20
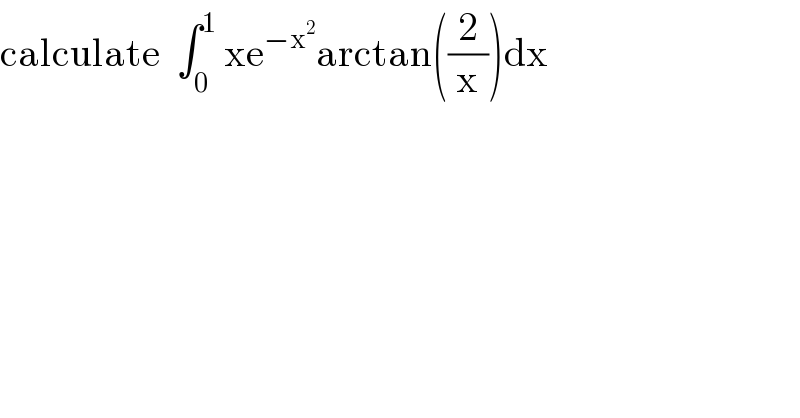
Answered by maths mind last updated on 23/Jun/20
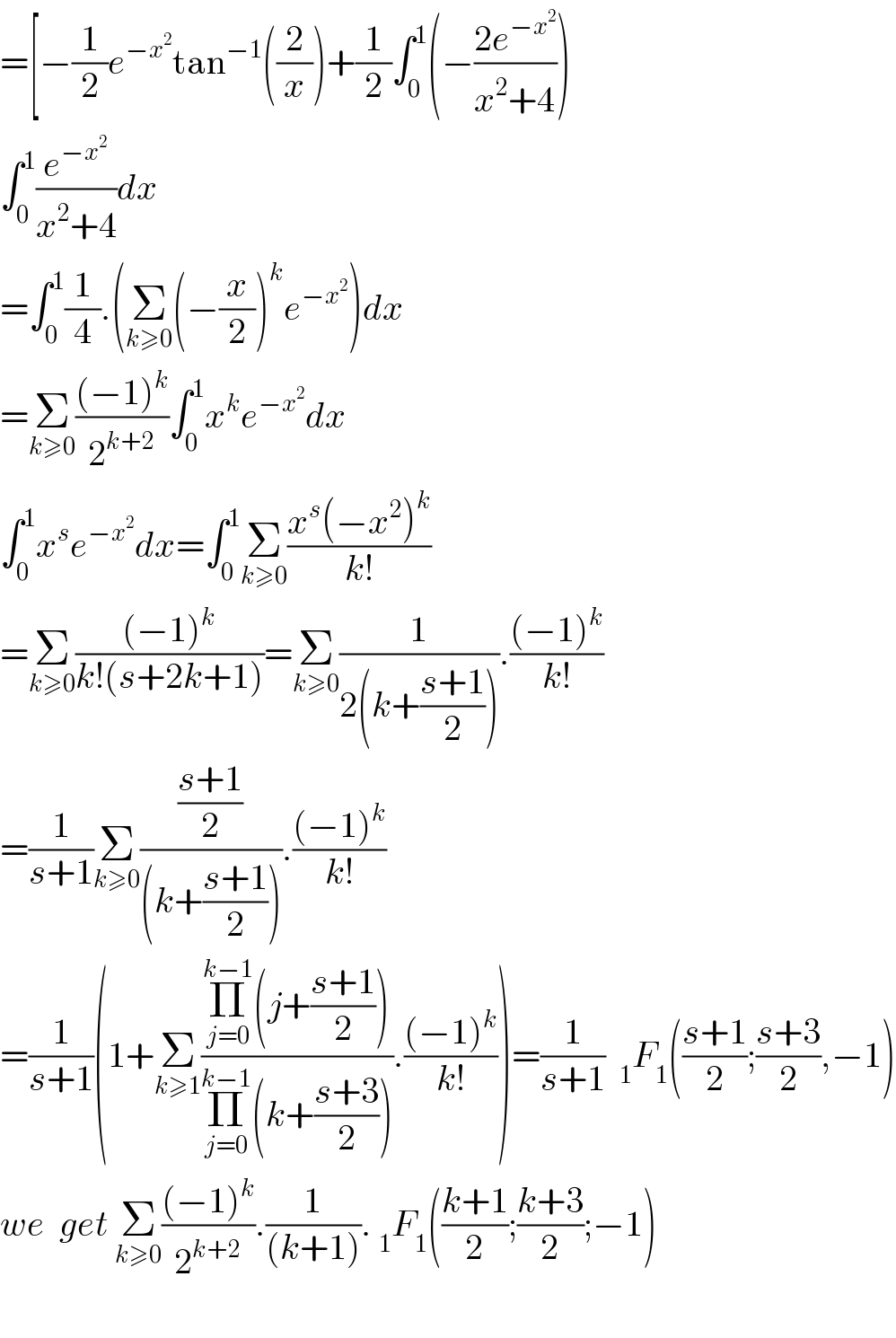
Commented by mathmax by abdo last updated on 23/Jun/20

Commented by maths mind last updated on 23/Jun/20

| ||
Question and Answers Forum | ||
Question Number 99824 by mathmax by abdo last updated on 23/Jun/20 | ||
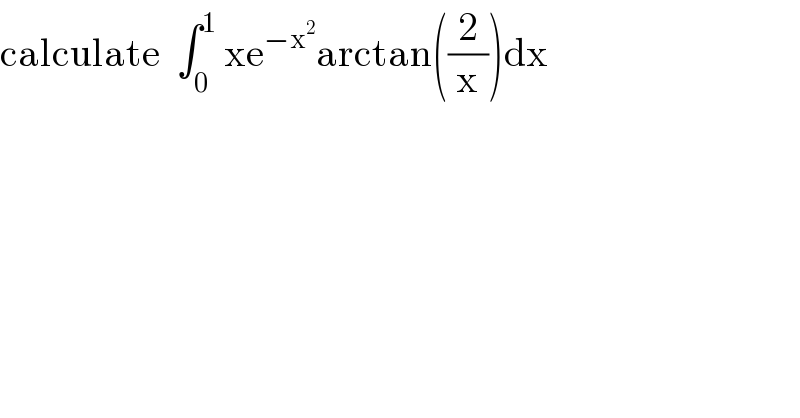 | ||
Answered by maths mind last updated on 23/Jun/20 | ||
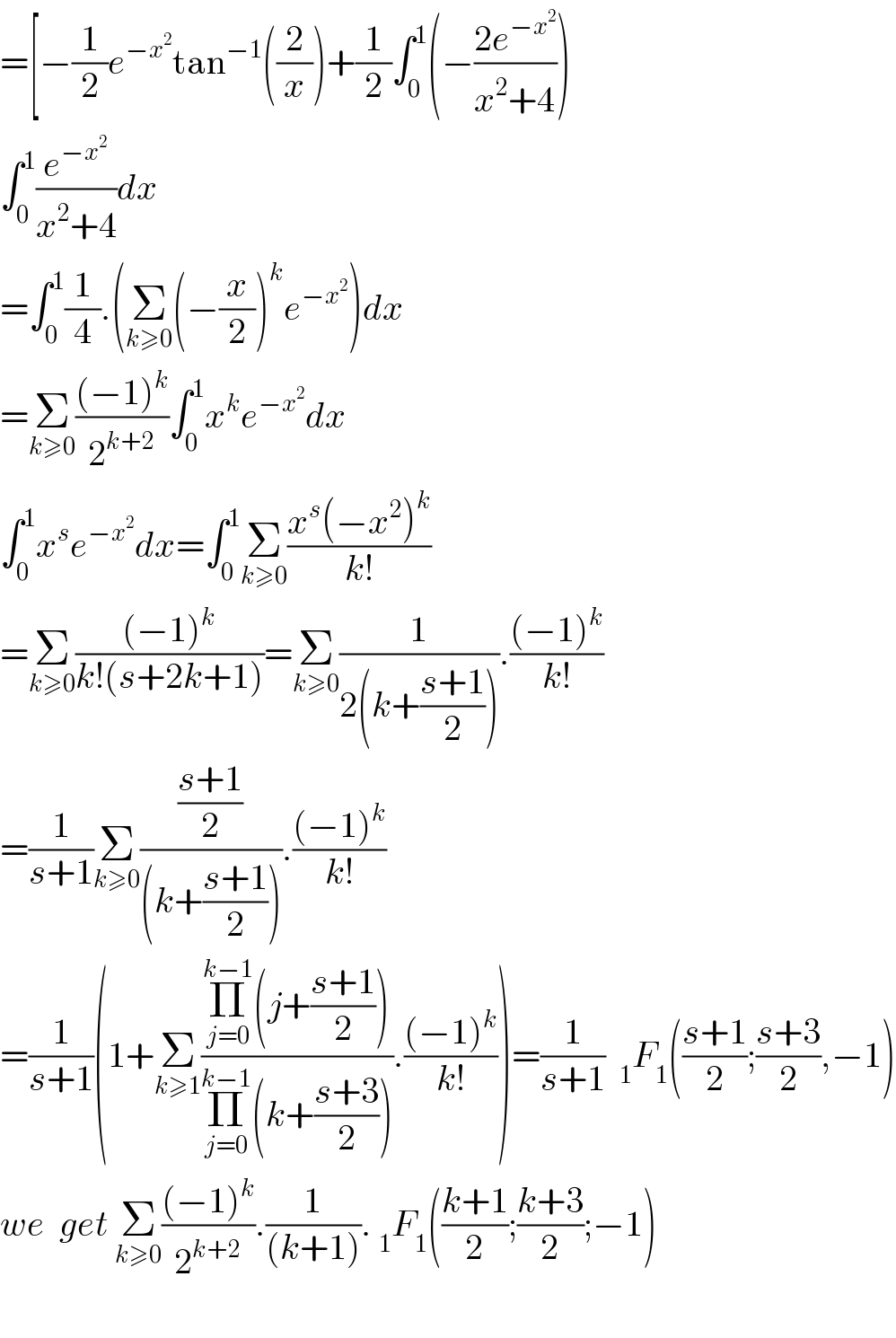 | ||
| ||
Commented by mathmax by abdo last updated on 23/Jun/20 | ||
 | ||
Commented by maths mind last updated on 23/Jun/20 | ||
 | ||