Previous in Relation and Functions Next in Relation and Functions
Question Number 99839 by mathmax by abdo last updated on 23/Jun/20
$$\mathrm{let}\:\mathrm{x}_{\mathrm{0}} =\mathrm{1}\:\mathrm{and}\:\mathrm{x}_{\mathrm{n}+\mathrm{1}} =\mathrm{ln}\left(\mathrm{e}^{\mathrm{x}_{\mathrm{n}} } −\mathrm{x}_{\mathrm{n}} \right) \\ $$$$\left.\mathrm{1}\right)\:\mathrm{prove}\:\mathrm{that}\:\mathrm{x}_{\mathrm{n}} \:\rightarrow\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\mathrm{prove}\:\mathrm{that}\:\Sigma\:\mathrm{x}_{\mathrm{n}} \:\mathrm{converges}\:\mathrm{and}\:\mathrm{ddyermine}\:\mathrm{its}\:\mathrm{sum} \\ $$
Commented by bachamohamed last updated on 23/Jun/20
$$\boldsymbol{{do}}\:\boldsymbol{{you}}\:\boldsymbol{{have}}\:\boldsymbol{{the}}\:\boldsymbol{{solution}}\:?\:\boldsymbol{{spead}}\:\boldsymbol{{the}}\:\boldsymbol{{solution}}\:\boldsymbol{{for}}\:\boldsymbol{{us}}. \\ $$
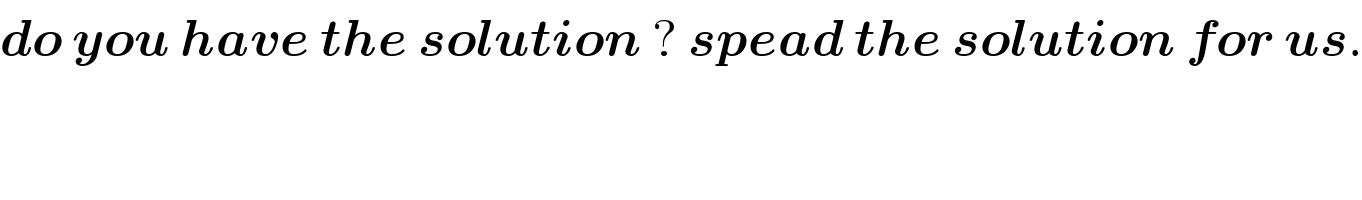
Commented by abdomathmax last updated on 23/Jun/20
$$\mathrm{you}\:\mathrm{must}\:\mathrm{take}\:\mathrm{a}\:\mathrm{try}\:\mathrm{sir}\:\mathrm{first}... \\ $$
Commented by bachamohamed last updated on 23/Jun/20
$$\mathrm{yes}\:\mathrm{i}\:\mathrm{tried}\:\mathrm{and}\:\mathrm{did}\:\mathrm{not}\:\mathrm{succed}\: \\ $$$$\mathrm{we}\:\mathrm{await}\:\mathrm{your}\:\mathrm{anser}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 23/Jun/20
$$\mathrm{nevermind}\:\mathrm{we}\:\mathrm{are}\:\mathrm{here}\:\mathrm{for}\:\mathrm{help}... \\ $$
Answered by maths mind last updated on 23/Jun/20
![1) shiw x_n cv let show x_n ≥0 we havef(x)=e^x −x−1 is increasing for x≥0 1≥x_0 =1≥0 supose≥1 x_n ≥0⇒≥f(1)≥f(x_n )≥f(0)=0⇒e^x_n −x_n ≥1⇒ln(e^x_n −x_n )≥0 f(1)=e^1 −1−1≤1⇒x_(n+1) ≤1 ⇒1≥x_(n+1) ≥0⇒by induction ∀n∈N 1≥ x_n ≥0 x_(n+1) −x_n =ln(e^x_n −x_n )−x_n =ln(e^x_n −x_n )−ln(e^x_n ) since e^x_n −x_n ≤e^(xn) ⇒x_(n+1) ≤x_n ⇒x_n is bounded and deacrease ⇒cv l=lim_(n→∞) X_n ⇒ln(e^l −l)=l⇒e^l −l=e^l ⇒l=0 x_(n+1) =ln(e^x_n −x_n ) n→∞ x_n →0 e^x_n =1+x_n +(((x_n )^2 )/2)+0(x_n ^2 )⇒e^(xn) −x_n =1+(x_n ^2 /2) x_(n+1) =ln(1+(x_n ^2 /2)+o(x_n ^2 )) =(x_n ^2 /2)+0(x_n ^2 )⇒∃c∈]0,1[ such ⇒x_(n+1) ≤cx_n ^2 =(cx_n )x_n since x_n →0⇒∃N ∀n≥N x_n <(1/2) ⇒x_(n+1) ≤(c/2)x_n ⇒x_n ≤((c/2))^(n−N) ,∀n≥N ⇒Σx_n =Σ_(n≤N) x_n +Σ_(n>N) x_n first finite 2nd by comparaison withe cv geoemtry serie ⇒Σx_n Cv it Sum i worcking on it](Q99854.png)
$$\left.\mathrm{1}\right) \\ $$$${shiw}\:{x}_{{n}} \:{cv}\: \\ $$$${let}\:{show}\:{x}_{{n}} \geqslant\mathrm{0} \\ $$$$\:{we}\:{havef}\left({x}\right)={e}^{{x}} −{x}−\mathrm{1}\:{is}\:\:\:{increasing}\:{for}\:{x}\geqslant\mathrm{0} \\ $$$$\mathrm{1}\geqslant{x}_{\mathrm{0}} =\mathrm{1}\geqslant\mathrm{0} \\ $$$${supose}\geqslant\mathrm{1}\:{x}_{{n}} \geqslant\mathrm{0}\Rightarrow\geqslant{f}\left(\mathrm{1}\right)\geqslant{f}\left({x}_{{n}} \right)\geqslant{f}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{e}^{{x}_{{n}} } −{x}_{{n}} \geqslant\mathrm{1}\Rightarrow{ln}\left({e}^{{x}_{{n}} } −{x}_{{n}} \right)\geqslant\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)={e}^{\mathrm{1}} −\mathrm{1}−\mathrm{1}\leqslant\mathrm{1}\Rightarrow{x}_{{n}+\mathrm{1}} \leqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}\geqslant{x}_{{n}+\mathrm{1}} \geqslant\mathrm{0}\Rightarrow{by}\:{induction}\:\forall{n}\in\mathbb{N}\:\mathrm{1}\geqslant\:{x}_{{n}} \geqslant\mathrm{0} \\ $$$${x}_{{n}+\mathrm{1}} −{x}_{{n}} ={ln}\left({e}^{{x}_{{n}} } −{x}_{{n}} \right)−{x}_{{n}} ={ln}\left({e}^{{x}_{{n}} } −{x}_{{n}} \right)−{ln}\left({e}^{{x}_{{n}} } \right) \\ $$$${since}\:{e}^{{x}_{{n}} } −{x}_{{n}} \leqslant{e}^{{xn}} \Rightarrow{x}_{{n}+\mathrm{1}} \leqslant{x}_{{n}} \\ $$$$\Rightarrow{x}_{{n}} \:\:{is}\:{bounded}\:{and}\:{deacrease}\:\Rightarrow{cv}\: \\ $$$${l}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{X}_{{n}} \Rightarrow{ln}\left({e}^{{l}} −{l}\right)={l}\Rightarrow{e}^{{l}} −{l}={e}^{{l}} \Rightarrow{l}=\mathrm{0} \\ $$$${x}_{{n}+\mathrm{1}} ={ln}\left({e}^{{x}_{{n}} } −{x}_{{n}} \right) \\ $$$${n}\rightarrow\infty\:{x}_{{n}} \rightarrow\mathrm{0} \\ $$$${e}^{{x}_{{n}} } =\mathrm{1}+{x}_{{n}} +\frac{\left({x}_{{n}} \right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{0}\left({x}_{{n}} ^{\mathrm{2}} \right)\Rightarrow{e}^{{xn}} −{x}_{{n}} =\mathrm{1}+\frac{{x}_{{n}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$${x}_{{n}+\mathrm{1}} ={ln}\left(\mathrm{1}+\frac{{x}_{{n}} ^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}_{{n}} ^{\mathrm{2}} \right)\right) \\ $$$$\left.=\frac{{x}_{{n}} ^{\mathrm{2}} }{\mathrm{2}}+\mathrm{0}\left({x}_{{n}} ^{\mathrm{2}} \right)\Rightarrow\exists{c}\in\right]\mathrm{0},\mathrm{1}\left[\:\:{such}\right. \\ $$$$\Rightarrow{x}_{{n}+\mathrm{1}} \leqslant{cx}_{{n}} ^{\mathrm{2}} =\left({cx}_{{n}} \right){x}_{{n}} \\ $$$${since}\:{x}_{{n}} \rightarrow\mathrm{0}\Rightarrow\exists{N}\:\forall{n}\geqslant{N}\:\:\:{x}_{{n}} <\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}_{{n}+\mathrm{1}} \leqslant\frac{{c}}{\mathrm{2}}{x}_{{n}} \Rightarrow{x}_{{n}} \leqslant\left(\frac{{c}}{\mathrm{2}}\right)^{{n}−{N}} ,\forall{n}\geqslant{N} \\ $$$$\Rightarrow\Sigma{x}_{{n}} =\underset{{n}\leqslant{N}} {\sum}{x}_{{n}} +\underset{{n}>{N}} {\sum}{x}_{{n}} \\ $$$${first}\:{finite}\:\mathrm{2}{nd}\:{by}\:{comparaison}\:{withe}\:{cv}\:{geoemtry}\:{serie} \\ $$$$\Rightarrow\Sigma{x}_{{n}} \:\:{Cv} \\ $$$${it}\:{Sum}\:{i}\:{worcking}\:{on}\:{it} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by abdomathmax last updated on 23/Jun/20
$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
Answered by abdomathmax last updated on 23/Jun/20
$$\left.\mathrm{2}\right)\:\mathrm{let}\:\mathrm{complete}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{x}_{\mathrm{n}} \rightarrow\mathrm{0}\:\left(\mathrm{n}\rightarrow\infty\right)\:\mathrm{and}\:\mathrm{e}^{\mathrm{x}_{\mathrm{n}+\mathrm{1}} } \:=\mathrm{e}^{\mathrm{x}_{\mathrm{n}} } −\mathrm{x}_{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{x}_{\mathrm{n}} =\mathrm{e}^{\mathrm{x}_{\mathrm{n}} } −\mathrm{e}^{\mathrm{x}_{\mathrm{n}+\mathrm{1}} } \:\:\mathrm{let}\:\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{x}_{\mathrm{k}} \:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(\mathrm{e}^{\mathrm{x}_{\mathrm{k}} } −\mathrm{e}^{\mathrm{x}_{\mathrm{k}+\mathrm{1}} } \right)\:=\mathrm{e}^{\mathrm{x}_{\mathrm{0}} } −\mathrm{e}^{\mathrm{x}_{\mathrm{1}} } +\mathrm{e}^{\mathrm{x}_{\mathrm{1}} } −\mathrm{e}^{\mathrm{x}_{\mathrm{2}} } +.... \\ $$$$+\mathrm{e}^{\mathrm{x}_{\mathrm{n}} } −\mathrm{e}^{\mathrm{x}_{\mathrm{n}+\mathrm{1}} } \:=\mathrm{e}−\mathrm{e}^{\mathrm{x}_{\mathrm{n}+\mathrm{1}} } \:\rightarrow\mathrm{e}−\mathrm{1}\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:=\mathrm{e}−\mathrm{1} \\ $$
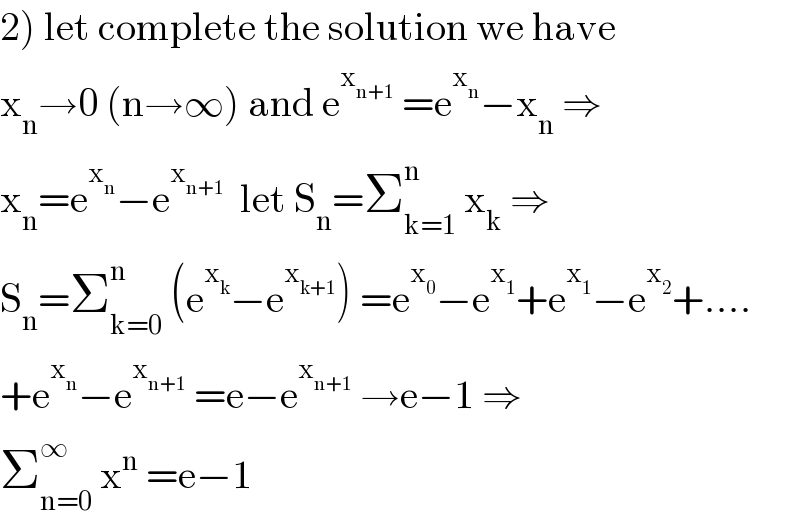
Commented by abdomathmax last updated on 23/Jun/20
$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}_{\mathrm{n}} =\mathrm{e}−\mathrm{1} \\ $$
Commented by bachamohamed last updated on 23/Jun/20
$$\mathrm{thank}'\mathrm{s}\:\mathrm{sir}\: \\ $$
Commented by mathmax by abdo last updated on 23/Jun/20
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}. \\ $$