Question Number 99887 by mr W last updated on 23/Jun/20
Commented by mr W last updated on 23/Jun/20
$${Additional}\:{question}: \\ $$$${Find}\:{the}\:{minimum}\:{initial}\:{velocity}\:{v} \\ $$$${such}\:{that}\:{the}\:{small}\:{block}\:{can}\:{reach} \\ $$$${the}\:{right}\:{end}\:{of}\:{the}\:{bigger}\:{block}. \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jun/20
$${Time}=\left(\sqrt{\frac{\mathrm{4}{Ml}}{\left({M}+{m}\right)\mu{g}}}\right) \\ $$$${velocity}_{{min}} =\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left({M}+{m}\right)\mu{gl}}{{M}}} \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jun/20
$${Sir}\:{i}\:{have}\:{not}\:{done}\:{it}\:{properly}.\:{I}\:{am}\:{trying}. \\ $$
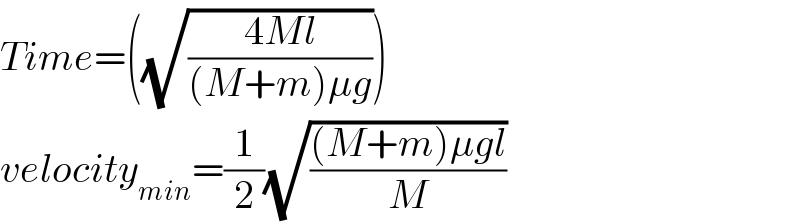
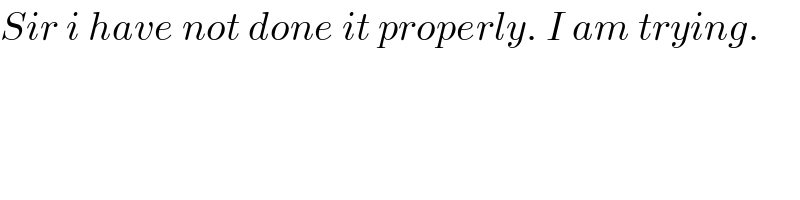
Commented by Dwaipayan Shikari last updated on 23/Jun/20
Sir can you show your prove?
Commented by mr W last updated on 24/Jun/20
$${i}\:{got}\:{a}\:{solution}\:{which}\:{i}\:{think}\:{is} \\ $$$${correct}.\:{see}\:{below}. \\ $$
Answered by ajfour last updated on 24/Jun/20
Commented by ajfour last updated on 24/Jun/20
$${frame}\:{of}\:{reference}:\:{bigger}\:{block} \\ $$$$−\mu\left({M}+{m}\right){g}+\frac{\mu}{\mathrm{2}}\left({mg}\right)=−{MA} \\ $$$${mA}=\frac{\mu{mg}}{\mathrm{2}{M}}\left(\mathrm{2}{M}+{m}\right) \\ $$$${f}=\frac{\mu{mg}}{\mathrm{2}} \\ $$$${mA}−{f}={ma} \\ $$$${a}={A}−\frac{\mu{g}}{\mathrm{2}}\:=\:\frac{\mu{g}}{\mathrm{2}}\left\{\mathrm{2}+\frac{{m}}{{M}}−\mathrm{1}\right\} \\ $$$${a}=\frac{\mu{g}\left({M}+{m}\right)}{\mathrm{2}{M}} \\ $$$${l}=\frac{\mathrm{1}}{\mathrm{2}}{at}^{\mathrm{2}} \:\:\:\Rightarrow\:\:\:{t}=\sqrt{\frac{\mathrm{4}{Ml}}{\mu\left({M}+{m}\right){g}}} \\ $$$${still}\:{thinking}\:{about}\:{v}_{{min}} ..... \\ $$
Answered by mr W last updated on 24/Jun/20
![a, u=acc. & velocity of mass m A, U=acc. & velocity of mass M ma=−(μ/2)mg ⇒a=−((μg)/2) u=v−((μg)/2)t≥0 MA=((μmg)/2)−μ(M+m)g ⇒A=−μg(1+(m/(2M))) U=v−μg(1+(m/(2M)))t≥0 Δa=a−A=((μg)/2)(1+(m/M)) L=(1/2)(Δa)t^2 ⇒t=(√((2L)/(Δa)))=2(√(L/(μg(1+(m/M))))) ...(i) (i) is valid only if U=v−(2+(m/M))(√((μgL)/(1+(m/M))))≥0 v≥v_2 =(2+(m/M))(√((μgL)/(1+(m/M)))) that means if v≥v_2 , the smaller block reaches the right end of the bigger block before the bigger block stops. if v<v_2 , the bigger blocks stops before the small block reaches the right end. assume the small block moves the distance L_1 on the big block at time t_1 as the bigger block stops. after this moment the bigger block rests on the the road and the small block moves the remaining distance L−L_1 . U_1 =v−(2+(m/M))(√((μgL_1 )/(1+(m/M))))=0 t_1 =2(√(L_1 /(μg(1+(m/M))))) ⇒L_1 =(((1+(m/M))v^2 )/(μg(2+(m/M))^2 )) ⇒t_1 =((2v)/(μg(2+(m/M)))) u_1 =v−((μg)/2)t_1 =v−(v/(2+(m/M)))=((1+(m/M))/(2+(m/M)))v starting with this velocity the smaller block should be able to move the remaining distance L−L_1 . (1/2)mu_1 ^2 ≥((μmg(L−L_1 ))/2) u_1 ^2 ≥μg(L−L_1 ) (((1+(m/M))/(2+(m/M))))^2 v^2 ≥μg[L−(((1+(m/M))v^2 )/(μg(2+(m/M))^2 ))] (((1+(m/M))^2 +1+(m/M))/((2+(m/M))^2 ))v^2 ≥μgL ((1+(m/M))/(2+(m/M)))v^2 ≥μgL ⇒v≥(√((1+(1/(1+(m/M))))μgL)) i.e. v_(min) =(√((1+(1/(1+(m/M))))μgL)) <v_2 summary: if 0<v< (√((1+(1/(1+(m/M))))μgL)) , small block can′t reach the right end, both blocks stoped moving before. if (√((1+(1/(1+(m/M))))μgL)) ≤v<(2+(m/M))(√((μgL)/(1+(m/M)))) small block reaches the right end, but the big block stoped moving before. if v≥(2+(m/M))(√((μgL)/(1+(m/M)))) small block reaches the right end and the big block is also in motion at this moment.](Q100014.png)
$${a},\:{u}={acc}.\:\&\:{velocity}\:{of}\:{mass}\:{m} \\ $$$${A},\:{U}={acc}.\:\&\:{velocity}\:{of}\:{mass}\:{M} \\ $$$${ma}=−\frac{\mu}{\mathrm{2}}{mg} \\ $$$$\Rightarrow{a}=−\frac{\mu{g}}{\mathrm{2}} \\ $$$${u}={v}−\frac{\mu{g}}{\mathrm{2}}{t}\geqslant\mathrm{0} \\ $$$${MA}=\frac{\mu{mg}}{\mathrm{2}}−\mu\left({M}+{m}\right){g} \\ $$$$\Rightarrow{A}=−\mu{g}\left(\mathrm{1}+\frac{{m}}{\mathrm{2}{M}}\right) \\ $$$${U}={v}−\mu{g}\left(\mathrm{1}+\frac{{m}}{\mathrm{2}{M}}\right){t}\geqslant\mathrm{0} \\ $$$$ \\ $$$$\Delta{a}={a}−{A}=\frac{\mu{g}}{\mathrm{2}}\left(\mathrm{1}+\frac{{m}}{{M}}\right) \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{2}}\left(\Delta{a}\right){t}^{\mathrm{2}} \\ $$$$\Rightarrow{t}=\sqrt{\frac{\mathrm{2}{L}}{\Delta{a}}}=\mathrm{2}\sqrt{\frac{{L}}{\mu{g}\left(\mathrm{1}+\frac{{m}}{{M}}\right)}}\:\:\:...\left({i}\right) \\ $$$$\left({i}\right)\:{is}\:{valid}\:{only}\:{if} \\ $$$${U}={v}−\left(\mathrm{2}+\frac{{m}}{{M}}\right)\sqrt{\frac{\mu{gL}}{\mathrm{1}+\frac{{m}}{{M}}}}\geqslant\mathrm{0} \\ $$$${v}\geqslant{v}_{\mathrm{2}} =\left(\mathrm{2}+\frac{{m}}{{M}}\right)\sqrt{\frac{\mu{gL}}{\mathrm{1}+\frac{{m}}{{M}}}} \\ $$$${that}\:{means}\:{if}\:{v}\geqslant{v}_{\mathrm{2}} ,\:{the}\:{smaller}\:{block} \\ $$$${reaches}\:{the}\:{right}\:{end}\:{of}\:{the}\:{bigger} \\ $$$${block}\:{before}\:{the}\:{bigger}\:{block}\:{stops}. \\ $$$${if}\:{v}<{v}_{\mathrm{2}} ,\:{the}\:{bigger}\:{blocks}\:{stops}\:{before} \\ $$$${the}\:{small}\:{block}\:{reaches}\:{the}\:{right}\:{end}. \\ $$$${assume}\:{the}\:{small}\:{block}\:{moves}\:{the} \\ $$$${distance}\:{L}_{\mathrm{1}} \:{on}\:{the}\:{big}\:{block}\:{at}\:{time}\:{t}_{\mathrm{1}} \\ $$$${as}\:{the}\:{bigger}\:{block}\:{stops}.\:{after}\:{this} \\ $$$${moment}\:{the}\:{bigger}\:{block}\:{rests}\:{on}\:{the} \\ $$$${the}\:{road}\:{and}\:{the}\:{small}\:{block}\:{moves} \\ $$$${the}\:{remaining}\:{distance}\:{L}−{L}_{\mathrm{1}} . \\ $$$${U}_{\mathrm{1}} ={v}−\left(\mathrm{2}+\frac{{m}}{{M}}\right)\sqrt{\frac{\mu{gL}_{\mathrm{1}} }{\mathrm{1}+\frac{{m}}{{M}}}}=\mathrm{0} \\ $$$${t}_{\mathrm{1}} =\mathrm{2}\sqrt{\frac{{L}_{\mathrm{1}} }{\mu{g}\left(\mathrm{1}+\frac{{m}}{{M}}\right)}} \\ $$$$\Rightarrow{L}_{\mathrm{1}} =\frac{\left(\mathrm{1}+\frac{{m}}{{M}}\right){v}^{\mathrm{2}} }{\mu{g}\left(\mathrm{2}+\frac{{m}}{{M}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{2}{v}}{\mu{g}\left(\mathrm{2}+\frac{{m}}{{M}}\right)} \\ $$$${u}_{\mathrm{1}} ={v}−\frac{\mu{g}}{\mathrm{2}}{t}_{\mathrm{1}} ={v}−\frac{{v}}{\mathrm{2}+\frac{{m}}{{M}}}=\frac{\mathrm{1}+\frac{{m}}{{M}}}{\mathrm{2}+\frac{{m}}{{M}}}{v} \\ $$$${starting}\:{with}\:{this}\:{velocity}\:{the}\:{smaller} \\ $$$${block}\:{should}\:{be}\:{able}\:{to}\:{move}\:{the} \\ $$$${remaining}\:{distance}\:{L}−{L}_{\mathrm{1}} . \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mu}_{\mathrm{1}} ^{\mathrm{2}} \geqslant\frac{\mu{mg}\left({L}−{L}_{\mathrm{1}} \right)}{\mathrm{2}} \\ $$$${u}_{\mathrm{1}} ^{\mathrm{2}} \geqslant\mu{g}\left({L}−{L}_{\mathrm{1}} \right) \\ $$$$\left(\frac{\mathrm{1}+\frac{{m}}{{M}}}{\mathrm{2}+\frac{{m}}{{M}}}\right)^{\mathrm{2}} {v}^{\mathrm{2}} \geqslant\mu{g}\left[{L}−\frac{\left(\mathrm{1}+\frac{{m}}{{M}}\right){v}^{\mathrm{2}} }{\mu{g}\left(\mathrm{2}+\frac{{m}}{{M}}\right)^{\mathrm{2}} }\right] \\ $$$$\frac{\left(\mathrm{1}+\frac{{m}}{{M}}\right)^{\mathrm{2}} +\mathrm{1}+\frac{{m}}{{M}}}{\left(\mathrm{2}+\frac{{m}}{{M}}\right)^{\mathrm{2}} }{v}^{\mathrm{2}} \geqslant\mu{gL} \\ $$$$\frac{\mathrm{1}+\frac{{m}}{{M}}}{\mathrm{2}+\frac{{m}}{{M}}}{v}^{\mathrm{2}} \geqslant\mu{gL} \\ $$$$\Rightarrow{v}\geqslant\sqrt{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{{m}}{{M}}}\right)\mu{gL}} \\ $$$${i}.{e}.\:{v}_{{min}} =\sqrt{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{{m}}{{M}}}\right)\mu{gL}}\:<{v}_{\mathrm{2}} \\ $$$$ \\ $$$${summary}: \\ $$$${if}\:\mathrm{0}<{v}<\:\sqrt{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{{m}}{{M}}}\right)\mu{gL}}\:, \\ $$$${small}\:{block}\:{can}'{t}\:{reach}\:{the}\:{right}\:{end}, \\ $$$${both}\:{blocks}\:{stoped}\:{moving}\:{before}. \\ $$$$ \\ $$$${if}\:\sqrt{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{{m}}{{M}}}\right)\mu{gL}}\:\leqslant{v}<\left(\mathrm{2}+\frac{{m}}{{M}}\right)\sqrt{\frac{\mu{gL}}{\mathrm{1}+\frac{{m}}{{M}}}} \\ $$$${small}\:{block}\:{reaches}\:{the}\:{right}\:{end}, \\ $$$${but}\:{the}\:{big}\:{block}\:{stoped}\:{moving}\:{before}. \\ $$$$ \\ $$$${if}\:{v}\geqslant\left(\mathrm{2}+\frac{{m}}{{M}}\right)\sqrt{\frac{\mu{gL}}{\mathrm{1}+\frac{{m}}{{M}}}} \\ $$$${small}\:{block}\:{reaches}\:{the}\:{right}\:{end}\:{and} \\ $$$${the}\:{big}\:{block}\:{is}\:{also}\:{in}\:{motion}\:{at}\:{this} \\ $$$${moment}. \\ $$
Commented by ajfour last updated on 24/Jun/20
$${great}\:{work}\:{sir},\:{i}\:{shall}\:{try}\:{to} \\ $$$${follow},\:{and}\:{i}\:{knew}\:{beforehand} \\ $$$${it}\:{would}\:{go}\:{a}\:{bit}\:{lengthy}.. \\ $$