A particle P is moving on a circle under the action of only one force acting always towards fixed point O on the circumference. Find ratio of (d^2 φ/dt^2 ) and ((dφ/dt))^2 .


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 22145 by Tinkutara last updated on 11/Oct/17

$A particle P is moving on a circle under$ $the action of only one force acting$ $always towards fixed point O on the$ $circumference . Find ratio of \frac{d^{2} ϕ}{{d t}^{2}} and$ ${(\frac{d ϕ}{d t})}^{2} .$
Commented by Tinkutara last updated on 11/Oct/17

Commented by sma3l2996 last updated on 12/Oct/17

$w e h a v e \vec{F} = m \vec{a} \Leftrightarrow \vec{a} = - \frac{F}{m} \vec{u} . . . (i)$ $a n d \vec{O P} = 2 R c o s (ϕ) \vec{u}$ $s o \vec{v} (P) = \frac{d \vec{O P}}{d t} = 2 R [- \dot{ϕ} s i n (ϕ) \vec{u} + \dot{ϕ} c o s (ϕ) \vec{k}] = 2 R \dot{ϕ} (- s i n ϕ \vec{u} + c o s ϕ \vec{k})$ $a n d \vec{a} (P) = \frac{d \vec{v}}{d t} = 2 R [\overset{. .}{ϕ} (- s i n ϕ \vec{u} + c o s ϕ \vec{k}) + \dot{ϕ} (- \dot{ϕ} c o s ϕ \vec{u} - \dot{ϕ} s i n ϕ \vec{k} - \dot{ϕ} s i n ϕ \vec{k} - \dot{ϕ} c o s ϕ \vec{u})]$ $s o : \vec{a} = 2 R [(- \overset{. .}{ϕ} s i n ϕ - 2 \dot{ϕ}^{2} c o s ϕ) \vec{u} + (\overset{. .}{ϕ} c o s ϕ - 2 \dot{ϕ}^{2} s i n ϕ) \vec{k}] . . . (i i)$ $w e h a v e (i) = (i i)$ $s o$ $2 R (- \overset{. .}{ϕ} s i n ϕ - 2 \dot{ϕ}^{2} c o s ϕ) = \frac{- F}{m} a n d \overset{. .}{ϕ} c o s ϕ - 2 \dot{ϕ}^{2} s i n ϕ = 0$ $s o$ $\overset{. .}{ϕ} c o s ϕ = 2 \dot{ϕ}^{2} s i n ϕ \Leftrightarrow \overset{. .}{ϕ} = 2 \dot{ϕ}^{2} t a n (ϕ) . . . (3 i)$ $\overset{. .}{ϕ} s i n ϕ + 2 \dot{ϕ}^{2} c o s ϕ = \frac{F}{2 R m} . . . (4 i)$ $(3 i) \to (4 i) \Rightarrow 2 \dot{ϕ}^{2} t a n (ϕ) s i n (ϕ) + 2 \dot{ϕ}^{2} c o s ϕ = \frac{F}{2 R m}$ $2 \dot{ϕ}^{2} c o s ϕ (\frac{t a n (ϕ) s i n ϕ}{c o s ϕ} + 1) = \frac{F}{2 R m}$ $2 \dot{ϕ}^{2} c o s ϕ ({t a n}^{2} ϕ + 1) = \frac{F}{2 R m}$ ${(\frac{d ϕ}{d t})}^{2} = \dot{ϕ}^{2} = \frac{F}{4 R m} c o s ϕ$ $a n d \overset{. .}{ϕ} = 2 \dot{ϕ}^{2} t a n ϕ = 2 (\frac{F}{4 R m} c o s ϕ) t a n ϕ$ $s o : \frac{d^{2} ϕ}{{d t}^{2}} = \overset{. .}{ϕ} = \frac{F}{2 R m} s i n ϕ$
Commented by sma3l2996 last updated on 12/Oct/17

	Answered by ajfour last updated on 12/Oct/17

	$A l t e r n a t e s o l u t i o n :$ $l e t t h e ∠ a t C b e θ .$ $θ = 2 ϕ \Rightarrow ω = \frac{d θ}{d t} = 2 \frac{d ϕ}{d t} . . (i)$ ${(\frac{d ϕ}{d t})}^{2} = \frac{ω^{2}}{4} . . . (a)$ $α = \frac{d ω}{d t} = 2 \frac{d^{2} ϕ}{{d t}^{2}} \Rightarrow \frac{d^{2} ϕ}{{d t}^{2}} = \frac{α}{2} . . . (b)$ $(b) \div (a) w i l l g i v e$ $\frac{d^{2} ϕ / {d t}^{2}}{{(d ϕ / d t)}^{2}} = \frac{α / 2}{ω^{2} / 4} = \frac{2 α}{ω^{2}}$ $= \frac{2 m (α r)}{m (ω^{2} r)} = \frac{2 {m a}_{T}}{{m a}_{r}}$ $= \frac{2 F \sin ϕ}{F \cos ϕ} = 2 t a n ϕ .$
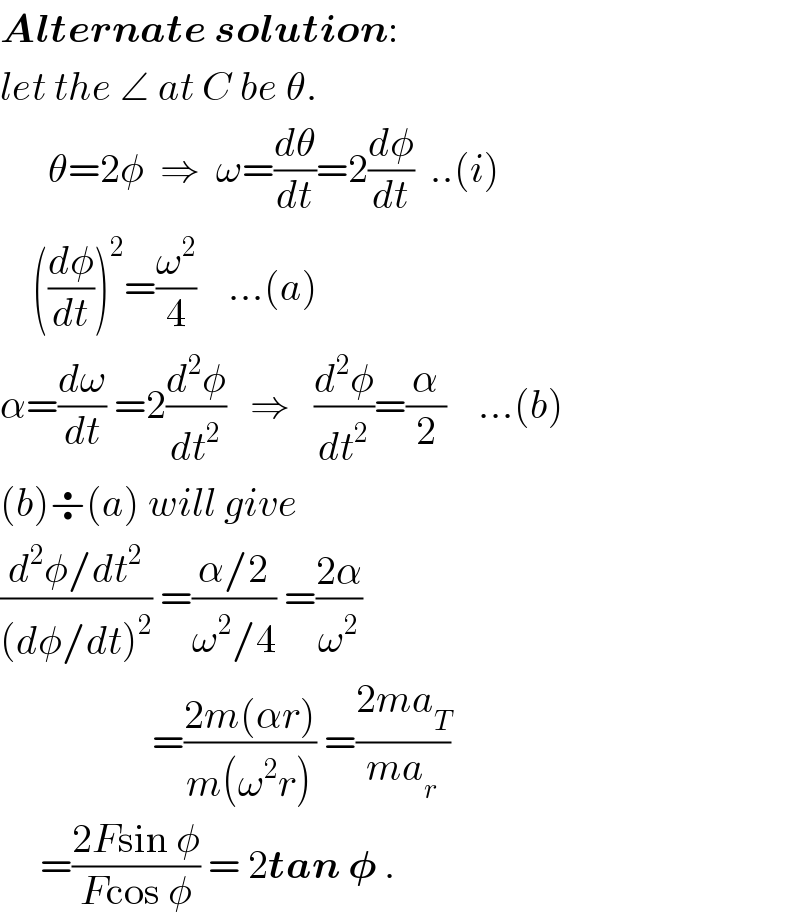
	Commented by Tinkutara last updated on 12/Oct/17

	$Thank you very much Sir!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum