
Question and Answers Forum
Question Number 147287 by mnjuly1970 last updated on 19/Jul/21
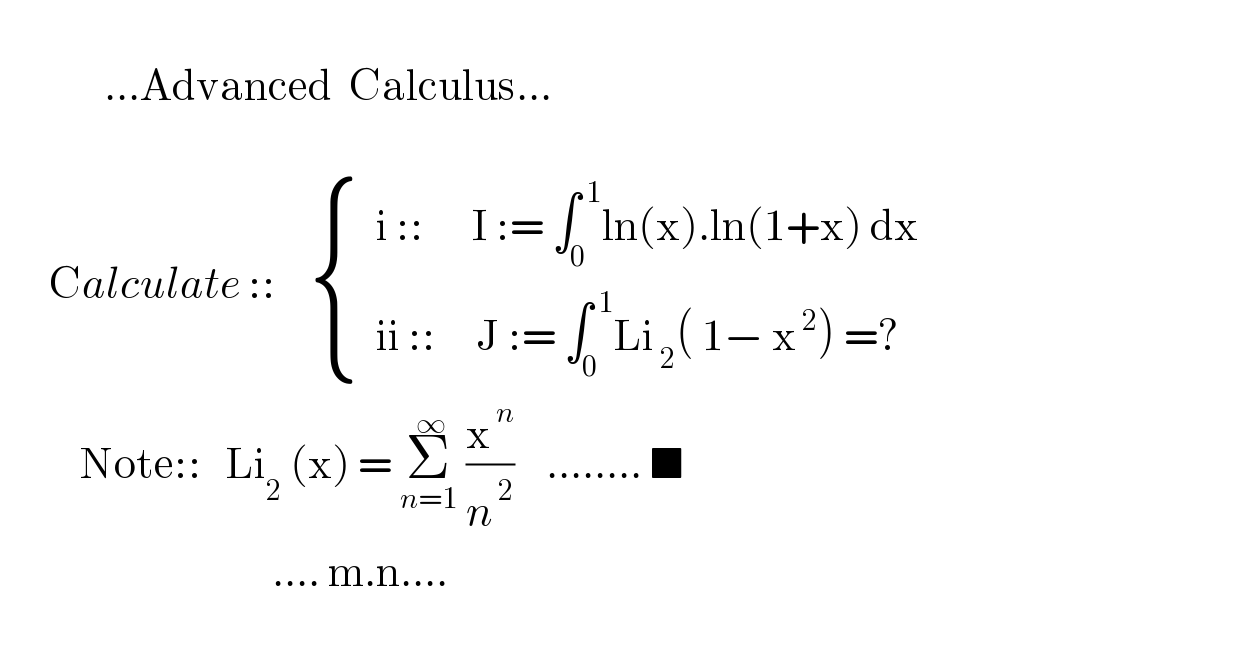
Answered by mindispower last updated on 19/Jul/21
![I=[(xln(x)−x)ln(1+x)]_0 ^1 −∫_0 ^1 ((xln(x))/(1+x))−(x/(1+x))dx =−ln(2)−∫_0 ^1 (((x+1−1)ln(x))/(1+x))−1+(1/(1+x))dx =−ln(2)−∫_0 ^1 ln(x)dx+∫_0 ^1 ((ln(x))/(1+x))dx+∫dx−∫(dx/(1+x)) =−ln(2)+1−∫_0 ^1 ((ln(1+x))/x)dx+1−ln(2) =−ln(2)−∫_0 ^1 ((ln(1−(−x)))/(−x))d(−x)+2 =ln(2)+[Li_2 (−x)]_0 ^1 =−2ln(2)+Li_2 (−1)+2=−ln(4)−(π^2 /(12))+2 J=[xli_2 (1−x^2 )]−∫_0 ^1 ((2x^2 ln(x^2 ))/(1−x^2 )) =−4∫_0 ^1 ((ln(x))/(1−x^2 ))dx+4∫_0 ^1 ln(x)dx =−2∫_0 ^1 ((ln(x))/(1−x))dx−2∫_0 ^1 ((ln(x))/(1+x))dx−4 =2Li_2 (1−x)]_0 ^1 +2∫_0 ^1 ((ln(1+x))/x)dx−4 =(π^2 /3)−2Li(−1)−4 =(π^2 /3)+(π^2 /6)−4=(π^2 /2)−4=(1/2)(π^2 −8)](Q147291.png)
Answered by mathmax by abdo last updated on 19/Jul/21
![Υ=∫_0 ^1 ln(x)ln(1+x)dx we have (d/dx)ln(1+x)=(1/(1+x))=Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x)=Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1))=Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) ⇒Υ=∫_0 ^1 (Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n))ln(x)dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 x^n ln(x)dx U_n =∫_0 ^1 x^n ln(x)dx=[(x^(n+1) /(n+1))ln(x)]_0 ^1 −∫_0 ^1 (x^n /(n+1))dx =−(1/((n+1)^2 )) ⇒Υ=−Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(n+1)^2 ))=Σ_(n=1) ^∞ (((−1)^n )/(n(n+1)^2 )) (1/(x(x+1)^2 ))=(a/x)+(b/(x+1))+(c/((x+1)^2 ))=h(x) a=1 ,c=−1 ,lim_(x→+∞) xh(x)=0=a+b ⇒b=−1 ⇒ h(x)=(1/x)−(1/(x+1))−(1/((x+1)^2 )) ⇒Υ=Σ_(n.1) ^∞ (((−1)^n )/n)−Σ_(n=1) ^∞ (((−1)^n )/(n+1)) −Σ_(n=1) ^∞ (((−1)^n )/((n+1)^2 )) we have Σ_(n=1) ^∞ (((−1)^n )/n)=−ln2 Σ_(n=1) ^∞ (((−1)^n )/(n+1))=Σ_(n=2) ^∞ (((−1)^(n−1) )/n)=ln(2)−1 Σ_(n=1) ^∞ (((−1)^n )/((n+1)^2 ))=Σ_(n=2) ^∞ (((−1)^(n−1) )/n^2 )=−Σ_(n=2) ^∞ (((−1)^n )/n^2 ) =−(Σ_(n=1) ^∞ (((−1)^n )/n^2 )+1)=−(2^(1−2) −1)ξ(2)−1=(1/2)(π^2 /6)−1=(π^2 /(12))−1 ⇒Υ=−ln2−ln2+1−(π^2 /(12))+1 =2−2ln2−(π^2 /(12))](Q147300.png)
| ||
Question and Answers Forum | ||
Question Number 147287 by mnjuly1970 last updated on 19/Jul/21 | ||
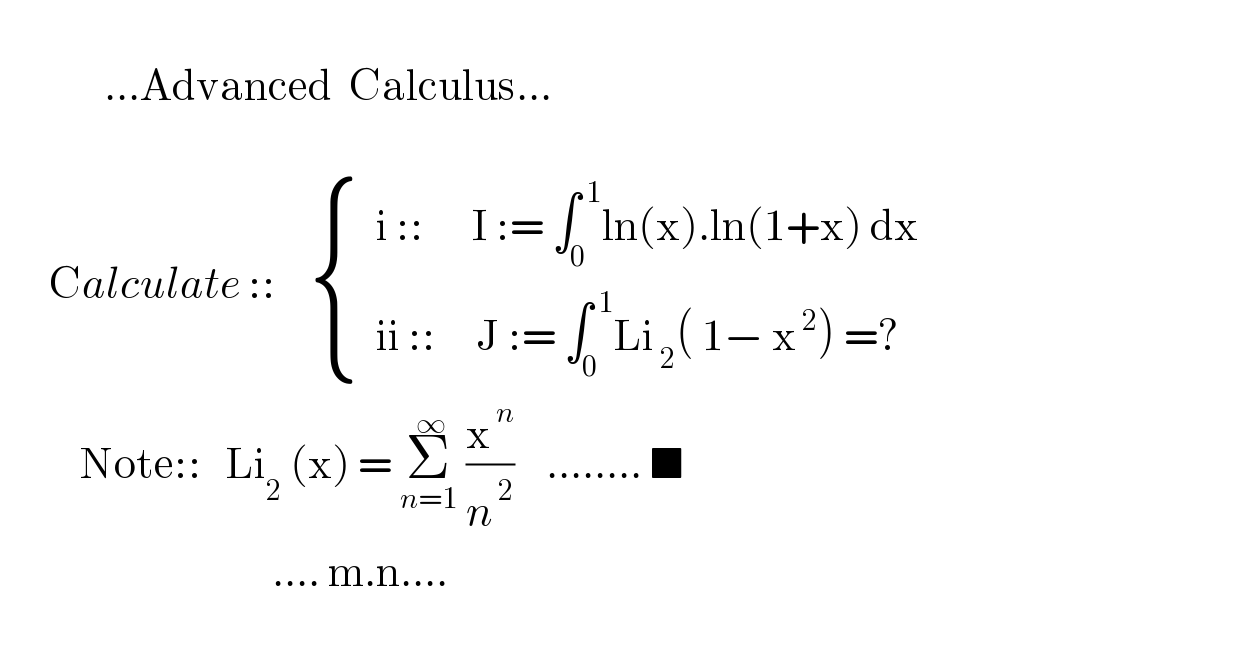 | ||
Answered by mindispower last updated on 19/Jul/21 | ||
![I=[(xln(x)−x)ln(1+x)]_0 ^1 −∫_0 ^1 ((xln(x))/(1+x))−(x/(1+x))dx =−ln(2)−∫_0 ^1 (((x+1−1)ln(x))/(1+x))−1+(1/(1+x))dx =−ln(2)−∫_0 ^1 ln(x)dx+∫_0 ^1 ((ln(x))/(1+x))dx+∫dx−∫(dx/(1+x)) =−ln(2)+1−∫_0 ^1 ((ln(1+x))/x)dx+1−ln(2) =−ln(2)−∫_0 ^1 ((ln(1−(−x)))/(−x))d(−x)+2 =ln(2)+[Li_2 (−x)]_0 ^1 =−2ln(2)+Li_2 (−1)+2=−ln(4)−(π^2 /(12))+2 J=[xli_2 (1−x^2 )]−∫_0 ^1 ((2x^2 ln(x^2 ))/(1−x^2 )) =−4∫_0 ^1 ((ln(x))/(1−x^2 ))dx+4∫_0 ^1 ln(x)dx =−2∫_0 ^1 ((ln(x))/(1−x))dx−2∫_0 ^1 ((ln(x))/(1+x))dx−4 =2Li_2 (1−x)]_0 ^1 +2∫_0 ^1 ((ln(1+x))/x)dx−4 =(π^2 /3)−2Li(−1)−4 =(π^2 /3)+(π^2 /6)−4=(π^2 /2)−4=(1/2)(π^2 −8)](Q147291.png) | ||
| ||
Answered by mathmax by abdo last updated on 19/Jul/21 | ||
![Υ=∫_0 ^1 ln(x)ln(1+x)dx we have (d/dx)ln(1+x)=(1/(1+x))=Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x)=Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1))=Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) ⇒Υ=∫_0 ^1 (Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n))ln(x)dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 x^n ln(x)dx U_n =∫_0 ^1 x^n ln(x)dx=[(x^(n+1) /(n+1))ln(x)]_0 ^1 −∫_0 ^1 (x^n /(n+1))dx =−(1/((n+1)^2 )) ⇒Υ=−Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(n+1)^2 ))=Σ_(n=1) ^∞ (((−1)^n )/(n(n+1)^2 )) (1/(x(x+1)^2 ))=(a/x)+(b/(x+1))+(c/((x+1)^2 ))=h(x) a=1 ,c=−1 ,lim_(x→+∞) xh(x)=0=a+b ⇒b=−1 ⇒ h(x)=(1/x)−(1/(x+1))−(1/((x+1)^2 )) ⇒Υ=Σ_(n.1) ^∞ (((−1)^n )/n)−Σ_(n=1) ^∞ (((−1)^n )/(n+1)) −Σ_(n=1) ^∞ (((−1)^n )/((n+1)^2 )) we have Σ_(n=1) ^∞ (((−1)^n )/n)=−ln2 Σ_(n=1) ^∞ (((−1)^n )/(n+1))=Σ_(n=2) ^∞ (((−1)^(n−1) )/n)=ln(2)−1 Σ_(n=1) ^∞ (((−1)^n )/((n+1)^2 ))=Σ_(n=2) ^∞ (((−1)^(n−1) )/n^2 )=−Σ_(n=2) ^∞ (((−1)^n )/n^2 ) =−(Σ_(n=1) ^∞ (((−1)^n )/n^2 )+1)=−(2^(1−2) −1)ξ(2)−1=(1/2)(π^2 /6)−1=(π^2 /(12))−1 ⇒Υ=−ln2−ln2+1−(π^2 /(12))+1 =2−2ln2−(π^2 /(12))](Q147300.png) | ||
| ||