
Question and Answers Forum
Question Number 138521 by mnjuly1970 last updated on 14/Apr/21

Answered by Dwaipayan Shikari last updated on 14/Apr/21
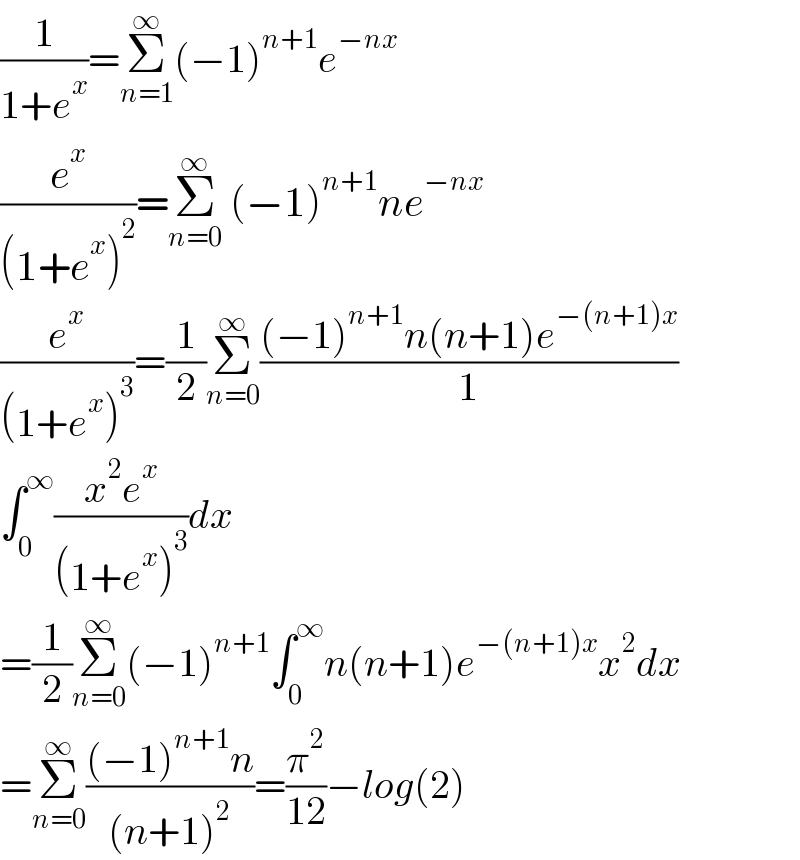
Answered by mathmax by abdo last updated on 14/Apr/21
![Φ=∫_0 ^∞ ((x^2 e^x )/((1+e^x )^3 ))dx ⇒Φ=_(e^x =t) ∫_1 ^∞ ((ln^2 t .t)/((1+t)^3 ))(dt/t) =∫_1 ^∞ ((ln^2 t)/((1+t)^3 )) =_(t=(1/u)) −∫_0 ^1 ((ln^2 u)/((1+(1/u))^3 ))(−(du/u^2 )) =∫_0 ^1 ((ln^2 u)/(u^2 (1+u)^3 )).u^3 du =∫_0 ^1 ((uln^2 u)/((1+u)^3 ))du =∫_0 ^1 (((1+u−1)ln^2 u)/((1+u)^3 ))du =∫_0 ^1 ((ln^2 u)/((1+u)^2 ))du−∫_0 ^1 ((ln^2 u)/((1+u)^3 ))du by parts ∫_0 ^1 ((ln^2 u)/((1+u)^2 ))du =[(1−(1/(1+u)))ln^2 u]_0 ^1 −∫_0 ^(1 ) (1−(1/(1+u)))((2lnu)/u)du =−2∫_0 ^1 ((lnu)/(1+u))du =−2 ∫_0 ^1 lnuΣ_(n=0) ^∞ (−1)^n u^n du =−2Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 u^n lnu du U_n =∫_0 ^1 u^n lnu du =[(u^(n+1) /(n+1))lnu]_0 ^1 −∫_0 ^1 (u^n /(n+1))du =−(1/((n+1)^2 )) ⇒∫_0 ^1 ((log^2 u)/((1+u)^2 ))du =2Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) =−2Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−2(2^(1−2) −1)ξ(2) =−2(−(1/2)).(π^2 /6)=(π^2 /6) ∫_0 ^1 ((log^2 x)/((1+x)^3 ))dx =∫_0 ^1 (1+x)^(−3) log^2 x dx by parts f^′ =(1+x)^(−3) and g=log^2 x ⇒ f=(1/(−2))(1+x)^(−2) ⇒∫_0 ^1 ((log^2 x)/((1+x)^3 ))dx={((1/2)−(1/(2(1+x)^2 )))log^2 x]_0 ^1 −∫_0 ^1 ((1/2)−(1/(2(1+x)^2 )))((2logx)/x)dx =−∫_0 ^1 (1−(1/((1+x)^2 )))((logx)/x)dx =−∫_0 ^1 (((1+2x+x^2 −1)/((1+x)^2 )))((logx)/x)dx =−∫_0 ^1 (((x+2)logx)/((1+x)^2 ))dx....be continued...](Q138557.png)
| ||
Question and Answers Forum | ||
Question Number 138521 by mnjuly1970 last updated on 14/Apr/21 | ||
 | ||
Answered by Dwaipayan Shikari last updated on 14/Apr/21 | ||
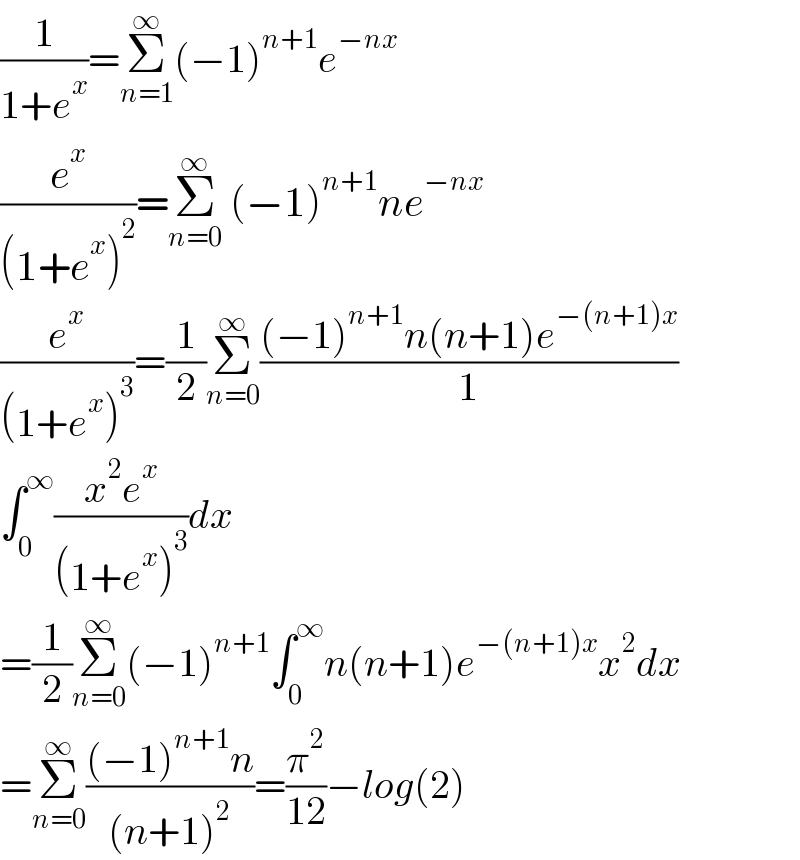 | ||
| ||
Answered by mathmax by abdo last updated on 14/Apr/21 | ||
![Φ=∫_0 ^∞ ((x^2 e^x )/((1+e^x )^3 ))dx ⇒Φ=_(e^x =t) ∫_1 ^∞ ((ln^2 t .t)/((1+t)^3 ))(dt/t) =∫_1 ^∞ ((ln^2 t)/((1+t)^3 )) =_(t=(1/u)) −∫_0 ^1 ((ln^2 u)/((1+(1/u))^3 ))(−(du/u^2 )) =∫_0 ^1 ((ln^2 u)/(u^2 (1+u)^3 )).u^3 du =∫_0 ^1 ((uln^2 u)/((1+u)^3 ))du =∫_0 ^1 (((1+u−1)ln^2 u)/((1+u)^3 ))du =∫_0 ^1 ((ln^2 u)/((1+u)^2 ))du−∫_0 ^1 ((ln^2 u)/((1+u)^3 ))du by parts ∫_0 ^1 ((ln^2 u)/((1+u)^2 ))du =[(1−(1/(1+u)))ln^2 u]_0 ^1 −∫_0 ^(1 ) (1−(1/(1+u)))((2lnu)/u)du =−2∫_0 ^1 ((lnu)/(1+u))du =−2 ∫_0 ^1 lnuΣ_(n=0) ^∞ (−1)^n u^n du =−2Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 u^n lnu du U_n =∫_0 ^1 u^n lnu du =[(u^(n+1) /(n+1))lnu]_0 ^1 −∫_0 ^1 (u^n /(n+1))du =−(1/((n+1)^2 )) ⇒∫_0 ^1 ((log^2 u)/((1+u)^2 ))du =2Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) =−2Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−2(2^(1−2) −1)ξ(2) =−2(−(1/2)).(π^2 /6)=(π^2 /6) ∫_0 ^1 ((log^2 x)/((1+x)^3 ))dx =∫_0 ^1 (1+x)^(−3) log^2 x dx by parts f^′ =(1+x)^(−3) and g=log^2 x ⇒ f=(1/(−2))(1+x)^(−2) ⇒∫_0 ^1 ((log^2 x)/((1+x)^3 ))dx={((1/2)−(1/(2(1+x)^2 )))log^2 x]_0 ^1 −∫_0 ^1 ((1/2)−(1/(2(1+x)^2 )))((2logx)/x)dx =−∫_0 ^1 (1−(1/((1+x)^2 )))((logx)/x)dx =−∫_0 ^1 (((1+2x+x^2 −1)/((1+x)^2 )))((logx)/x)dx =−∫_0 ^1 (((x+2)logx)/((1+x)^2 ))dx....be continued...](Q138557.png) | ||
| ||