
Question and Answers Forum
AlgebraQuestion and Answers: Page 226





Pg 221 Pg 222 Pg 223 Pg 224 Pg 225 Pg 226 Pg 227 Pg 228 Pg 229 Pg 230
|
Question and Answers Forum |
AlgebraQuestion and Answers: Page 226 |
| { ((x^3 +y^2 =a)),((x^2 +y^3 =b)) :} [solve for:x,y,a≠b∈R] |

|

|
| solving the following system of equations { ((((3x−y)/(x−3y))=x^2 )),((((3y−z)/(y−3z))=y^2 )),((((3z−x)/(z−3x))=z^2 )) :} |

|
| Find all pair(x,y) of real numbers that are the solutions to the system { ((x^4 +2x^3 −y=−(1/4)+(√3))),((y^4 +2y^3 −x=−(1/4)−(√3))) :} |
| Solve in real numbers the equation (x)^(1/(3 )) + ((x−1))^(1/(3 )) + ((x+1))^(1/(3 )) = 0 |
| evaluate: I = ∫_0 ^( 1) (((x+1)/x))^(x!) dx |
| evaluate: I = ∫_1 ^( ∞) ((1/x))^x dx |
| Let f be a real-valued function defined on the inte- rval [−1, 1]. If the area of the equilateral triangle with (0, 0) and (x, f(x)) as two vertices is (√3)/4, then f(x) is equal to (A) (√(1−x^2 )) (B) (√(1+x^2 )) (C) −(√(1−x^2 )) (D) −(√(1+x^2 )) |
| Examples of functions such that f(x+y)=f(x)+f(y) for all x,y∈R |
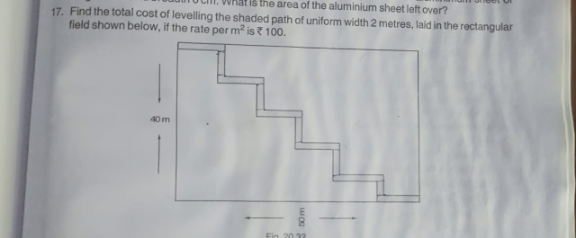
| If f:R→R is a function such that f(0)=1 and f(x+f(y))= f(x)+y for all x, y∈R, then (A) 1 is a period of f (B) f(n)=1 for all integers n (C) f(n)=n for all integers n (D) f(−1)=0 |
| Q1 Let M_2 be the set of square matrices of order 2 over the real number system and R={(A,B)∈M_2 ×M_2 ∣A=P^( T) BP for some non-singular P ∈M} Then R is (A) symmetric (B) transitive (C) reflexive on M_2 (D) not an equivalence relation on M_2 Q2 For any integer n, let I_n be the interval (n, n+1). Define R={(x, y)∈R∣both x, y ∈ I_n for some n∈Z} Then R is (A) reflexive on R (B) symmetric (C) transitive (D) an equivalence relation |
| Solve in real numbers the system of equations { (((3x+y)(x+3y)(√(xy)) =14)),(((x+y)(x^2 +14xy+y^2 )= 36)) :} |

|
| For any integer n, let I_n be the interval (n, n+1). Define R={(x, y)∈R∣both x, y ∈ I_n for some n∈Z} Then R is (A) reflexive on R (B) symmetric (C) transitive (D) an equivalence relation |
| If 3x+(1/(2x))=6 find 8x^3 +(1/(27x^3 )) |
| If a function f:R→R satisfies the relation f(x+1)+f(x−1)=(√3)f(x) for all x∈R then a period of f is (A) 10 (B) 12 (C) 6 (D) 4 |
| Q1 If f:R→R is defined by f(x)=[x]+[x+(1/2)]+[x+(2/3)]−3x+5 where [x] is the integral part of x, then a period of f is (A) 1 (B) 2/3 (C) 1/2 (D) 1/3 Q2 Let a<c<b such that c−a=b−c. If f:R→R is a function satisfying the relation f(x+a)+f(x+b)=f(x+c) for all x∈R then a period of f is (A) (b−a) (B) 2(b−a) (C) 3(b−a) (D) 4(b−a) |
| Given k ∈ N. 1) justify these relations: 3^(2k) +1≡2[8] and 3^(2k+1) +1≡4[8]. 2) Given (E): 2^n −3^m =1. n and m are unknowed. • Show that if m is even , (E) does not have solution. ■ Deduct from the first question 1) that the couple (2;1) is the only solution of (E). |
|

|

|
| Let a<c<b such that c−a=b−c. If f:R→R is a function satisfying the relation f(x+a)+f(x+b)=f(x+c) for all x∈R then a period of f is (A) (b−a) (B) 2(b−a) (C) 3(b−a) (D) 4(b−a) |
| Let a>0 and f:R→R a function satisfying f(x+a)=1+[2−3f(x)+3f(x)^2 −f(x)^3 ]^(1/3) for all x∈R. Then a period of f(x) is ka where k is a positive integer whose value is (A)1 (B)2 (C)3 (D)4 |
| If the roots of the equation 24x^4 −52x^3 +18x^2 +13x−6=0 are α , −α , β and (1/β). Find the value of α and β. |
Pg 221 Pg 222 Pg 223 Pg 224 Pg 225 Pg 226 Pg 227 Pg 228 Pg 229 Pg 230 |